
英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
统计方法来评估建筑物耗电量的变化
Xavier Serrano-Guerrero a,lowast;, Guillermo Escrivaacute;-Escrivaacute;b, Carlos Roldaacute;n-Blayb
a Grupo de Investigacioacute;n en Energiacute;as, Universidad Politeacute;cnica Salesiana, Elia Liut y Calle Vieja, 010103, Cuenca, Ecuador
b Institute for Energy Engineering, Universitat Politegrave;cnica de Valegrave;ncia, Camino de Vera, s/n, Edificio 8E, escalera F, 2° piso, 46022, Valencia, Spain
摘 要
本文已经做出许多努力来定义模式、预测,和预测能源使用。然而,能量消耗的变化可以使用各种方法进行详细研究。这项工作提出了一种统计方法来评估设施的变化。消耗模式根据预定时间间隔的历史数据库根据日的类型(星期几,工作或非工作)获得,并且提出评估电气工程概况中的变化的指标。通过评估这些变化,可以将这些值与设施中的可能事件关联起来,这些事件可以用于在能源管理系统中生成警报,并降低成本和维护周期。此外,本文还介绍了应用测试表的多标准解释,该解释提供解释,并找出可能的异常原因。
copy;2018Elsevier B.V.保留所有权利。
文章历史:
2017年10月6日收到
2017年12月5日修订
2017年12月23日接受
2018年1月12日在线提供
关键词:消费概况 消费中的变化 电气模式 楼宇管理
1.介绍
本文已经做出了一些研究来减少世界各地建筑物对能源的需求和使用。从建筑材料,热通风空调系统(HVAC),照明系统[1],使用可再生能源,改变设备以提高效率[2],需求管理[3],分布式发电与清洁能源的集成[4]等角度研究能效。与提高建筑节能相关的最重要的努力之一是“零能耗建筑”的概念,该建议提出建筑物在可再生能源中自给自足以避免将二氧化碳排放到环境中[5]。
对能源行为(模式)的分析对提出提高能源效率的行动至关重要。能量模型是从统计的角度出发[6],包括多元回归分析和主成分分析[7]。研究人员已经对能源模式进行了统计分析[8-11],可以将不同用途的类似消费聚类在一起,例如监测,对消费者进行分类或根据日期类型分析功率。此外,使用这些方法,可以预测消费者,交易商,公用事业或发电机的功耗。
术语预测和预测在文献中的含义时是不同的[3,12-15]。术语预测是统计模型的输出,即使数据是历史数据。预测指的是对未来值的预测。预测建筑能量的方法在[12]中概述,它们被分组为:简化设计的工程方法;统计方法;人工智能(特别是神经网络);支持向量机(SVM);和支持向量回归(SVR)。SVR通常用于分类和解决回归问题[13]。变量及其特征的选择可能与数据分析中应用的统计方法同样重要。然而,关键变量的应用在能源消耗分析和建模中很少[16]。影响能量的因素很多,因此分析可能很复杂。在[17]中,它被表示为在统计学习时机器学习机器性能特征选择特征子组件的选择学习方法被应用。
在文献中许多作者指出,已经做出了许多努力来定义模式,预测和预测能源使用;然而,对能源变化的识别和量化尚未深入评估。这项工作提供了一个统计评估,用于识别SAICC方法的变化,以检测分析期间电气工程的变化。将分析的日期与先前从预定时间间隔的历史数据库中获得的模式进行比较。计算变化指数(IoC)以对分析日期的变化进行编目并使用多标准解释表,推断异常的原因。
评估配置文件中的更改可将这些值与设施中可能发生的异常事件相关联。这可以用于生成警报,降低维护成本并快速响应异常。
本文组织如下。第2节解释了实施方法。第3节介绍了拟议统计方法的应用和验证。最后,在第4节中得出一些结论。
2.建议的统计方法
本文提出了一种统计方法(SAICC方法)来分析和修改设施中的电气系统。
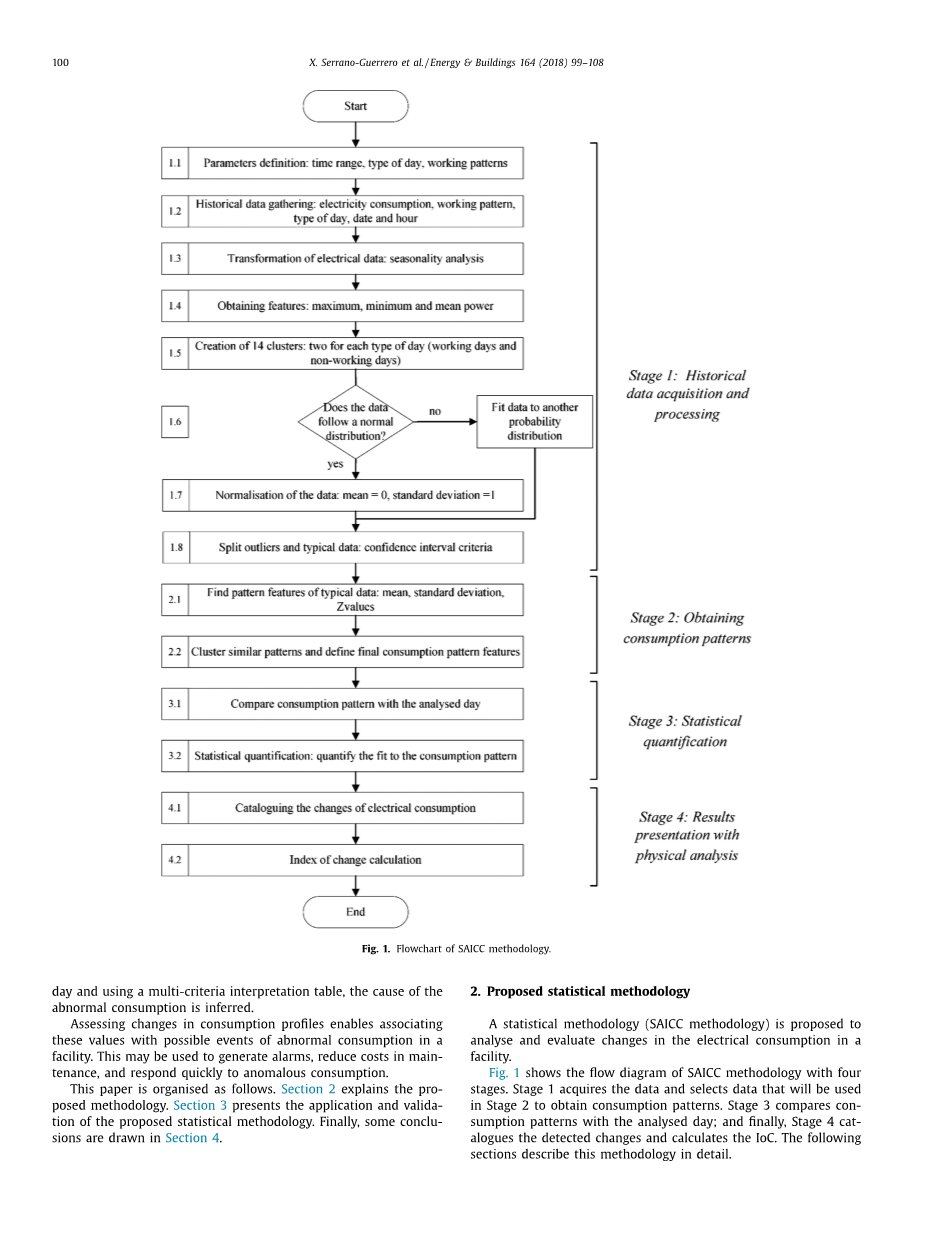
图1显示了四个阶段的SAICC方法流程图。
图1 四个阶段的SAICC方法流程图
阶段1获取数据并选择将在阶段2中使用的数据以获得最佳模式。阶段3压缩模式与分析日期;最后,阶段4对检测到的变化进行编目并计算IoC。以下各节详细介绍了这种方法。
2.1. 阶段l:历史数据采集和处理
2.1.1 . 参数定义
最初建立应用方法学来获取模式的分析参数。 并定义了时间范围(天数),日期类型(星期几)以及工作模式一个工作日(WD)或非工作日(NWD)。
2.1.2. 历史数据收集
方法中使用的历史数据以矩阵(MxN)组织。 其中M表示获得模式的时间范围内的天数,N表示每天考虑的参数数目。
对于本研究,最大分析间隔为一年,因为认为这些模式随时间而变化,数据是使用Derd系统[3]从安装在巴伦西亚理工大学(UPV)的功率计获得的,所以M = 365。
考虑的参数是15分钟间隔的电能,日期和小时,日类型(星期几)和工作模式(WD或NWD),所以N=99。
2.1.3. 电气数据的转换
由于许多原因,建筑物中的电能会随时间变化,包括外部温度变化,工作操作,假期等等。在进行年度数据分析时,如果分析间隔大于三个月,则有必要对数据进行转换,以使季节性不反映异常数据[9]。
对于季节性分析,获得WD值的功率数据向量并计算基本负载值。基础负荷值是用整个分析周期的第1个百分点的值获得的。在分析数据时,作者确定概率分布的左尾存在不到1%的异常值,因此使用这个百分数忽略与非常事件(如停电)相关的异常值。由于基本负载是在非工作小时(NWH)产生的,并且不影响季节性分析,所以从WD的原始功率数据矢量中减去基本负载值。然后将移动平均方法应用于数据矢量,以获得用于获得去季节化矢量的季节性指标[18]。最后,将基本负载值添加到此矢量。在季节性分析中不考虑NWD,因为当建筑物空置时,能源消耗保持不变。
2.1.4. 获取功能
在此步骤中,每个日期数据都会添加三列带有功能的列。在这项工作中,每天添加最大,平均和最小的权力。每日能量不被视为一项功能,因为它与平均功率直接相关(相关性等于1)。因此,数据矩阵的维数为Mtimes;N#39;,其中N#39;=102。
2.1.5. 创建14个集群
矩阵MxN#39;被分割成14个解聚矩阵,两个(WD或NWD)每周的每一天(图2)。 数据是分开的评分:首先,仅使用nec数据处理更多数据每次手术都要进行;其次,因为那时的数据是如果一天中的一种模式是容易聚集的类似于另一个。这为该方法提供了更强的稳健性。
图2 分解矩阵
2.1.6. 正态分布分析
有必要证明数据是否具有正态分布在分解矩阵中,每个小时(列)。证明一个数据正态分布,卡方拟合优度检验被使用[19]。
(1)
其中:
X2是偶数变量的值,其采样分布近似于具有k-1自由度的卡方分布。
k是班级间隔的数量。
oi 和ei分别表示i值的观测和预期频率。
在这项研究中,所做的测试得出的结论是“数据遵循正态分布的零假设不是被拒绝”。因此,对于以下阶段,它被认为是数据遵循正态分布。
2.1.7. 数据的规范化
一旦证明数据遵循正态分布,使得平均值等于零(mu;= 0),并且标准偏差等于1(sigma;= 1),则将分解矩阵标准化。
规范化程序逐列进行。 如果矩阵的行数超过30(考虑的天数),则标准差的统计值近似于实际标准偏差[19]。 计算每个数据值(每列)的Z值(表达式2):
(2)
其中:
Xrc是行r和列c中变量(在分解矩阵中)的值,uc是列c中值的平均值,最后sigma;c是列c中值的标准偏差。
每列中Z的最大值是Zmax向量,而每列中Z的最小值是Zmin向量。
2.1.8. 拆分直播和典型数据
当一个值超出正态分布函数的95%置信区间时,该值被视为异常值。该过程针对每个分解矩阵的每一列进行。如果一个或多个N#39;值超出置信区间,则将一天分类为非典型。
一个值在置信区间内的概率表示为:
(3)
其中和分别是置信区间的上限和下限,而和分别表示正态分布的左右尾区域。
最后,这一步骤将数据分成两组:一组用于典型数据(没有异常值);第二个是非典型数据(带有异常值)。
2.2. 阶段2:获得消费模式
2.2.1. 查找模式功能
典型数据的数量代表了消费模式,并以每个分解矩阵的“模式矩阵”表示。 针对每种模式考虑的特征是:平均值;能耗数据的标准差;和Zmin和Zmax(Z维值)。
图3显示了一年中一周中每一天的典型值的平均值和标准差矢量。 在这种情况下,星期一至星期五被认为是WD,星期六和星期天是NWD。
图3 寻找模式特征,平均功率和标准偏差
2.2.2. 群集类似的模式
由于提供的数据可用,此步骤的目标是“分析日”。欧几里德距离组类似于该方法的模式如果已被用于聚类,则该方法的效果更好。向量A和B之间的欧几里德距离与元素数量n的定义如下:
(4)
在这项研究中,n = 96,每个值(ai和bi)代表15分钟间隔内的平均功率。
最终消费模式被称为“最终模式矩阵”,由定义模式特征的天数组成。为了获得这个矩阵,欧几里德距离计算在每个初始模式的均值和标准差的向量之间 每周的每一天。如果距离小于任意阈值,则模式被认为是相似的。最终的模式矩阵是通过将相似的模式分组得到的,并且再次计算模式特征。
在这项工作中,星期一至星期五的聚类形成由平均功率决定,而不是由标准偏差决定。表1显示了聚类过程的结果。
表1 聚类过程的结果
|
Nordm; |
集群 |
|
1 |
星期一 |
|
2 |
星期二----星期三----星期四 |
|
3 |
星期五 |
|
4 |
星期六----星期日 |
2.3. 阶段3:统计量化
2.3.1. 消费模式与分析日期
最终模式矩阵的定义变量可用作分析特定日子的耗电量的参考。分析的日期被定义为包含之前定义的N个列的行向量。
分析日的值使用以下公式进行转换:
(5)
其中Zi是Z值,i是索引列,xi是位置i的特征值。同时ui是平均值,sigma;i是“最终模式矩阵”第i列值的标准偏差。
一旦数据用公式(5),它可以表示在Z域中。
置信区间是可变的,因为Zmin,i和Zmax,i值在99个值中各不相同。显然,如果Zi处于置信区间内(Zmin,i lt;Zi lt;Zmax,i),则不会将其
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[467545],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


