橡胶门式起重机起重电动机的功率流动建模外文翻译资料

 2022-04-18 22:18:28

英语原文共 7 页，剩余内容已隐藏，支付完成后下载完整资料

橡胶门式起重机起重电动机的功率流动建模

Stefano Pietrosanti，IEEE会员;William Holderbaum，IEEE会员Victor M. Becerra，IEEE高级会员.

摘要：一种用于计算带有非平行电缆的橡胶起重机（RTG）的功率需求的方法已经被开发用于测量典型的升降循环中的能量消耗。从费利克斯托港的测量结果来看，已经观察到，在恒定的转子速度条件下，由于功率要求随容器高度增加而增加机械装置的特有几何特征。提升绳索角度的变化导致转矩负载和功耗的增加。通过使用从起重机的几何结构中提取的信息，可以计算给定容器的重量和垂直位置的势能增量。提升机上的负载转矩和物体的垂直速度已经计算出来，允许在以恒定的转速提升容器时对升降机电机功率消耗进行建模。所提出的模型已经与恒定的功率需求近似进行比较，对于40t以下的质量显示更高的精确度。

索引术语：负载流量分析，负载建模，数学模型，机械系统，电力系统建模。

一、导言

集装箱码头内的货物集装箱堆放由橡胶轮胎起重机（RTG）起重机处理，起重机的作用是将集装箱从码头拖拉机上提起并堆放在港口区域，等待被移到列车或船上。 RTG起重机通常采用柴油驱动，占船舶能源消耗量的重要比例，并且具有重要的分布式排放温室气体排放权[1]。目前，船舶港口正在考虑通过提高效率，改善运营和回收浪费的能源来减少能源消耗。起重机的起重电动机的额定功率高达400千瓦，占据了大部分的能量消耗，并且在降低容器时提供了回收潜在能量的机会[2]。建模这一要素的能量流对于提高效率并通过控制方法来实现能量利用至关重要。龙门起重机的起重机几何形状历来被塑造成单一起落式起重机，其动力方式被用来控制起重作业[3]。后来，研究问题转向采用并联电缆的多平面吊具[4]，[5]，这导致恒定转子速度下的稳态阶段的功耗不变。通过分析Felixstowe港口RTG起重机上获得的数据，观察到只能通过计算以恒定速度垂直移动质量所需的功率来模拟功率波形的形状，如图1所示，因为当电动机以恒定的速度提升容器时，功率需求增加。当降低容器时，也发生相同的行为，相反。这是由于使用不平行电缆的起重机起重机构的特殊几何形状，由于绳索的垂直角度不断变化而导致电力需求随着集装箱高度的增加而增加：当集装箱位于顶部时，电力消耗（每单位）由于绳索角度不同而更高。在文献[6]中，作者发现吊具的垂直速度随着绳索与通过它的垂直线之间的角度而变化。为了便于抑制振荡[7]，研究中的起重机配备了非平行绳索，从而形成了与本文中介绍的类似的几何结构。主要研究起重缆绳的几何形状，目的是减少摆动和摆动，同时在建模起重电动机的功率需求时也可以发现这些好处。考虑到非平行电缆的存在以及由此引起的功率需求不确定性，并且包含了对能量储存的控制[8]，[9]，尤其是在明确假设稳定状态下的恒定电力需求的工作中[2] [10]。由于在恒速阶段电力需求意外增加，因此很难实施一种专门为具有非平行起重机的平行电缆起重机而设计的控制策略。其他类型的起重机在电梯负载变化时具有相似的独特特征，如港口门式起重机一直是研究的主题[12]，但迄今为止，详细分析了具有非平行功能的RTG的功率消耗绳索仍然缺失。本文旨在通过在升降马达以恒定速度旋转时计算容器的垂直速度和加速度来解决该问题，假设可以测量重量的情况下可以准确地测量由马达提供的机械功率的负载。计算的输出可以与测量的电力流量进行比较以验证所提出的模型。现在可以估算任何集装箱运输的能耗和回收率，而无需在起重机上进行任何测量。本文是[13]的更新版本。

手稿于2015年7月20日收到; 2015年11月19日和2015年12月21日修订; 2016年2月5日接受。发布日期2016年2月11日;当前版本的日期为2016年5月18日。论文2015-PSEC-0583.R2于10月18日至22日在美国德克萨斯州Addison的IEEE工业应用协会年会上发布，并被批准在IEEE TRANSACTIONS ON INDUSTRY IEEE工业应用协会电力系统工程委员会的应用。这项工作是Climate KIC资助的SUSPORTS项目的一部分。S. Pietrosanti和W. Holderbaum与英国雷丁大学雷丁分校系统工程学院RG66AY联系（电子邮件s.pietrosanti@pgr.reading.ac.uk;w.holderbaum@reading.ac。英国）。 VM Becerra与英国雷丁大学Reading系统工程学院合作，现在他在英国普茨茅斯大学朴茨茅斯大学PO13DJ工程学院工作（电子邮件：victor.becerra@port. ac.uk）。本白皮书中一个或多个数据的彩色版本可在http://ieeexplore.ieee.org上在线获取。数字对象标识符10.1109 / TIA.2016.2529560

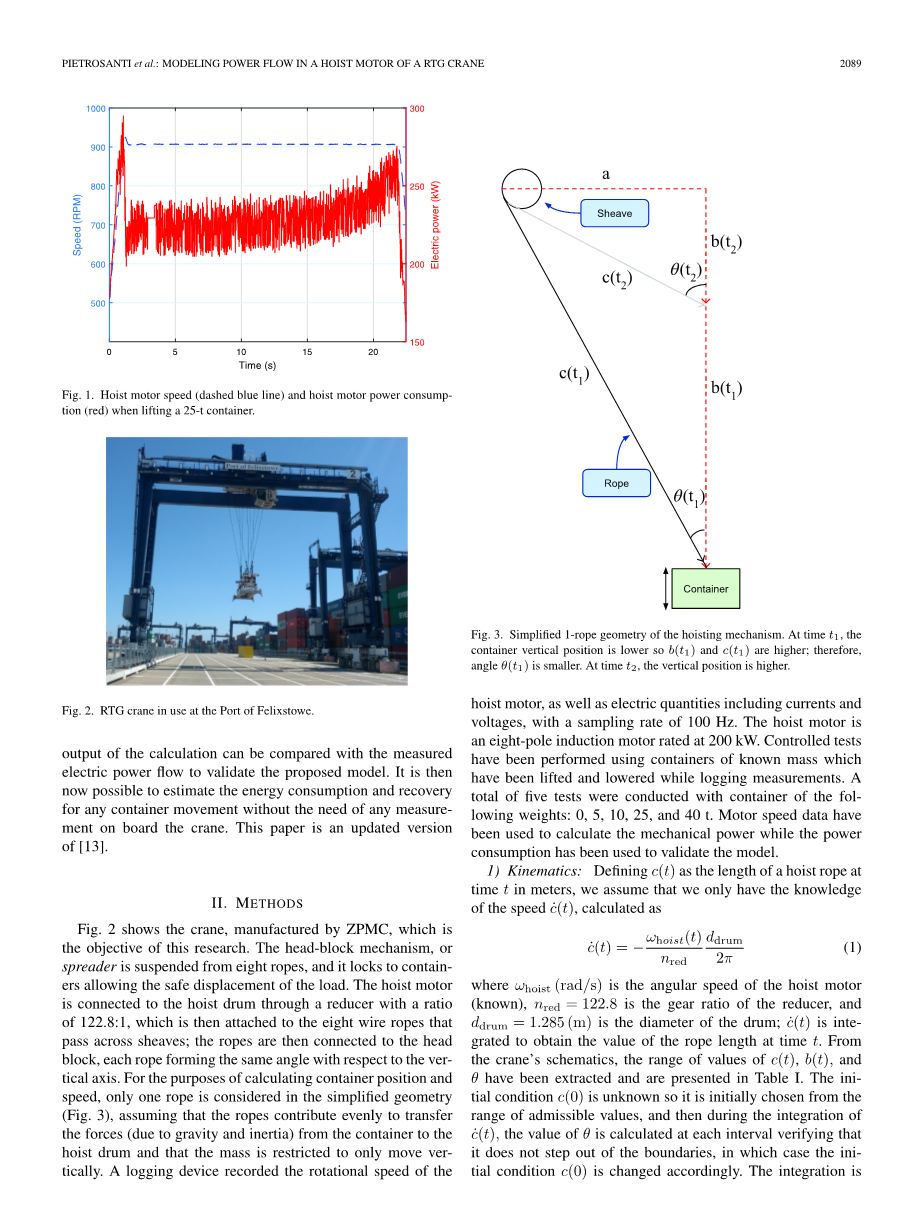
图1.提升25吨容器时的提升电机速度（蓝色虚线）和提升电机功耗（红色）。

图2.在Felixstowe港使用的RTG起重机。

二、方法

图2显示了由ZPMC制造的起重机，这是本研究的目标。 头块机构或吊具悬挂在八条绳索上，并锁定在允许安全移动货物的集装箱上。 起重马达通过比例为122.8：1的减速机连接到起重机卷筒，然后再连接到穿过滑轮的八根钢丝绳上; 然后将绳索连接到头部块，每个方向形成一个相对于垂直方向的角度。在计算容纳位置和速度时，假设绳索均匀地传递来自容器的力（由于重力和惯性），在简化几何体中只考虑一根绳索（图3）到提升鼓并且质量被限制为仅仅垂直移动。

一个记录设备记录了该转速电动机，包括电流和电压在内的绝对电介质，采样率为100 Hz。起重电动机是额定功率为200kW的八极感应电动机。使用在记录测量时被升降的已知质量的容器进行了受控测试。共进行了五次测试，使用下列重量的容器：0,5,10,25和40吨。电机速度数据已用于计算机械功率，而功耗则用于验证模型。

图3.提升机构的简化单绳几何。 在t1时刻，容器垂直位置较低，所以b（t1）和c（t1）较高; 因此，角度theta;（t1）较小。 在时间t2，垂直位置更高。

  1. 运动学：确定c（t）以米为单位的等时线的时间t，我们假设我们只知道速度（t），计算公式为:

其中omega;hoist（rad / s）是提升马达的角速度（已知），nred = 122.8是减速器的齿轮比，ddrum = 1.285（m）是滚筒的直径; c（t）被综合以获得时间t处绳索长度的值。 从起重机的原理图中可以看出，c（t），b（t）和theta;的取值范围已经被提取出来并列在表1中。初始条件c（0）是未知的，所以它最初是从允许值，然后在积分（t）期间，在每个间隔处计算theta;的值，以验证它不超出边界，在这种情况下，初始条件c（0）相应地改变。然后重新开始积分，并重复该循环直到找到合适的初始条件。

表一.测量的长度范围c，容器垂直位置b和纵向角度theta;。

从图3中的几何形状可以看出，c（t）的值与长度a和b（t）的值相关联，

从原理图中测得的值约为2.640米。 知道c（t）gt;aforall;t，垂直位置b（t）是以下等式：

那么容器（t）的速度就是:

方程（5）意味着当提升马达转速恒定[且c（t）不变]时，容器的垂直速度随绳索长度c（t）而变化。 集装箱的垂直速度和绳索速度的比值取决于c（t）

  1. 中的比率绘制在图4中，可以注意到，在升降马达速度恒定的情况下，垂直集装箱速度（t）随着c（t）的减小而增加。 角度theta;（t）随着容器垂直移动而变化，并且它可以容易地从a和c（t）计算出来，

垂直加速度可以通过进一步区分速度来计算:

图4.垂直速度与绳索速度之间的比率与绳索长度的关系。

图5.升降时升降马达对容器施加的力。

限制在恒定提升电动机速度阶段中的计算，即（t）= 0，（9）可以被简化:

垂直加速度根据容器的高度而变化，将用于计算电机的负载转矩。

  1. 动力学：为了计算升降马达功率流量，还需要负载转矩输入。 如前所述，当速度恒定时，功率消耗随容器高度增加。 电机机械功率Pm与扭矩T乘以旋转速度omega;成比例; 那么很明显，随高度变化的变量是扭矩。 在图5中，可以看出，扭矩T施加到提升鼓上，使其通过施加相等的力而提升容器F1和F2的总和导致向量FB。通过计算Fb和角度theta;的值，可以计算出电机需要施加到（已知直径的）鼓的扭矩。 矢量Fb是两个对称分量的总和

当水平分量抵消时，模量取决于垂直分量

与Fn，y是y轴上的组件Fn键。 可以根据theta;（t），a和c（t）的值（来自图3）来计算分量F1，y，

力矢量的大小F1需要应用来在容器上产生垂直力Fb.

静止时，升降马达需要补偿的唯一力量就是重力。 但是，当容器移动时，作用于质量的力的总和为

ms = 13000是头块和散布器的质量（kg），mc是容器的质量，g是由重力引起的加速度，（10）中计算得到的起升电动机施加的瞬时垂直加速度，b（t）是在正方向上的单向矢量。 鉴于直径ddrum，扭矩TD那么必须遵循以下步骤:

并且考虑到比率为nred的减速器的存在，升降马达必须提供以下瞬时负载转矩T：

当包含物时，b（t）= 0和作用在容器上的唯一加速度是重力

图6.计算绳索位置和容器垂直位置（起始块体），用于吊装10吨容器时的受控测试。

图7.升降10吨集装箱时，绳索和集装箱的速度叠加在起重马达的动力流上。

计算出的扭矩和速度值可以通过将其与消耗电力的测量值进行比较来验证。

三、结果与讨论

在费利克斯托港的起重机上进行的测量被用来提取集装箱的速度和加速度。 利用（1）式和（12）式的转矩，利用旋转电机的旋转速度计算出旋转位置和速度。

图6显示了用10吨容器对提升机运动进行受控测试时使用（1）和整合计算容器位置的结果。图7通过区分垂直位置计算的显示速度。 可以注意到速度非常接近额定值50m / min（由制造商提供）; 也可以验证升降马达（红色）中的功率流量随着计算的垂直位置而变化，尽管恒定的电机速度和负载质量也是如此。从（13）中可以计算出起重马达需要提供的转矩测试以保持10吨容器处于静止状态。

图8.由容器的质量和加速度以及系统的几何结构计算出的起重马达的负载扭矩。 一个10吨的容器被降低（首先23秒），然后再升高到大约相同的高度。 边界（红色）是计算转矩的理论最大值和最小值。

表2.为了将机械转换成电力的转换损失选择出来的值

表3.建议模型的RMSD值和常数幂近似值

给定（t）[和积分c（t）]的值,可以应用（12）来计算电动机上的负载转矩。结果如图8所示。计算转矩的灰色信号对提升转子速度测量中的噪声非常敏感;出于这个原因，它也显示了扭矩值的移动平均值。为了减轻噪音问题，可以使用恒定的电机转速作为输入; 在这项工作中，它是对计算的准确性进行测量的。 假设除了重力和绳索长度之外没有垂直加速度横跨整个允许范围，（12）表示在整个运动期间的预期平均速度大约为1191-1518牛米，证实了图8所示结果的有效性。

升降马达的瞬时功率消耗已经记录在叉车的端口上并且可以用于验证结果。感应马达的电力消耗随着升高集装箱所需的机械功率而增加，后者是负载转矩T（t）和转速omega;（t）之间的倍数，

其中Pm（t）是马达为了以特定速度移动集装箱而需要产生的瞬时机械功率，不包括电力损失和机械损失。 如果将这些损坏分为三个类别，则不可能将机械功率Pm（t）与电功率Pe（t）

其中a是解释取决于电功率大小（例如，铜损）的损失的倍增因子，b1与取决于速度的损失（例如，摩擦）相关联，并且b2是不依赖于 （t）包括机械功率建模误差和损失的高阶近似。通过比较所提模型的infin;（t）范数相对于幂级数逼近的可能性，证明了该模型的有效性。 表II中所示的参数a，b1和b2的值已经被选择为使模型和近似的归一化的均方根均方差（RMSD）||sigma;（t）|| 2最小化。

表3给出了每个测试的||（t）|| 2的结果值，并且图9显示了所提出的模型输出的例子与近似值的比较。其可以证明，所提出的模型仅具有对40吨容器的适用性的唯一测试，通过高误差（表III）资料[如图9（d）所示]。 在余下的测试中，RMSD低于近似值，模型跟踪功率需求。所提出的模型的噪声输出是由于升降机转子速度测量和突出问题的计算所致。正如第三节所述，使用恒定速度作为模型的输入而不是测量将消除这个问题。

  1. 结论

在RTG起重机的起重电机中测量功率流量表明恒速运动中的功率消耗意外增加。通过分析起重机的几何形状，可以模拟起重电动机提升集装箱所需的机械动力，包括起重机几何形状引起的负载扭矩和加速度的变化.Felixstowe所采用的对比模型输出和测量结果表明，对于loadtpt25t 。这些结果可用于评估起重马达和起重机本身的动力流量，从而分析能量消耗和降低已知重量的集装箱时的可回收能量的研究。掌握每个升降机所用能量的全部知识可能导致节能技术，包括使用的能源存储，这可以减少对集装箱处理最耗能的行业之一对环境和燃料成本的影响。

未来的研究可能包括电力系统动力学的建模，包括不可避免的损失，从而导致主电机功耗的更准确表示。

致谢

作者要感谢费利克斯托港提供数据。

<p

全文共8808字，剩余内容已隐藏，支付完成后下载完整资料</p

资料编号：[13706]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章