
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
有效十进制乘法VLSI实现的符号数值编码
摘要-十进制Xtimes;Y乘法是一个复杂的运算,其中中间部分乘积(IPPs)是从一组预先计算的基数-10 X倍数中选择的。有些作品只需要通过将Y的数字重新编码为有符号数字的在[-5,5]之间的一次热表示将[0,5] x X.这降低了选择逻辑,而代价是额外的IPP。2的补码符号数字(Tcd)编码通常用于表示ipp,其中在[-5,-1]之间的Y的重编码数字需要动态否定(通过每一位X倍数)。在本文中,尽管产生了17个IPP,对于16位操作数,我们成功地用16个IPP开始了部分乘积约简(PPR),从而提高了VLSI的正则性。此外,我们通过符号大小符号数字(Smsd)编码表示预先计算过的倍数,节省了75%的xors.。对于第一级PPR,我们设计了一个有效的加法器,它有两个SMSd输入数,其和用TCSD编码表示。此后,多级TCSD就导致了两个TCSD部分积的积累,最终经过一个特殊的早期转换,得到了最终的二进制编码十进制乘积。因此,SI实现了16times;16位并行十进制多进制.。综合评价结果表明,与以往的相关设计相比,性能有了一定的提高。
关键词-基数-10乘法器,冗余表示,符号大小有符号数字(SMSD),VLSI设计。
一、介绍
十进制算术硬件在货币、基于web和人类交互应用程序中快速处理十进制数据是非常需要的[1].特别是通过并行部分乘积生成(PPG)和部分乘积缩减(PPR),可以实现快速基数-10乘法,但在VLSI实现过程中,这两种方法的面积消耗很大。因此,在保持高速并行实现的同时,降低了硅的成本。
设表示ntimes;n十进制乘数,其中乘数X,乘数Y和乘积P是[0,9l之间正常的基数-10号数字。这些数字通常通过二进制编码的十进制(BCD)C编码表示。然而,中间部分产品(IPPS)表示通过一个多样性的经常重复的十进制数字集和编码(例如,[0,10]进位(CS)[2],超过小数[3]、[4],[-7,7][5],双4, 2, 2,1[6],和[8,8]).
选择可选的IPP表示与PPG无关,这在十进制零运算中具有特别重要的意义:一是IPP的快速、低成本平差,二是它对IPP表示的影响,这对PPR效率影响很大。通过bcd数字逐位乘法实现简单的ppg[8],[9]是慢的,昂贵的,并导致n双-BCD IPPs的ntimes;n乘法(即,2n BCD数被添加)。然而,[10]的工作既能增加乘数,也能使数字签名的数字(SMSD)表示,并使用更有效的3-b-b-PPG。尽管如此,经过长期的实践[11],大多数PPG方案使用预先计算的乘积倍数X(或X倍数)。完备集0,1,...9}乘X作为普通的bcd n的预计算和随后的选择也是缓慢和昂贵的.。一种常见的补救技术是使用一个较小的、成本较低的集合,通过快速无携带操作(例如,0、1、2、4、5}x)可以实现,而代价是将在PPR中添加的BCD数增加一倍;也就是说。生成N个双BCD IPPs,如3X=(2X,X),7X=(5X,2X)或9X=(5X,4X)。我们总结了PPG和PPR在第二节中的几个先前相关工作的特点(表一)。
乘数位的重新编码,在某些相关的作品中[4],[6],[7],[在乘法器的n位重编码数字之外,导致一个进位位,这将产生一个额外的部分乘积。这对于n=16的并行乘法(即根据IEEE标准单精度基数-10浮点数(12)的十进制数)来说尤其成问题,其中生成的17种部分产品需要5个PPR水平而不是4个(即1092 16)。此外,它们还根据乘子的编码数字符号动态地否定正倍数。这种技术减少了选择X倍数的逻辑的面积和延迟,而代价是有条件地否定所选倍数,而ntimes;n乘法至少需要个异或门。
在本文中,我们的目的是利用[-5,5]SMSD乘法器的重新编码和X倍数的动态否定,同时通过生成[-6,6]SMSd预先计算了X倍数(即每4b位数只有一个异或门)减少异或门的数目。下文重点介绍了本文件的其他贡献。
1)从16个部分乘积开始PPR:一个特殊的两个中间SMSd数字的动态增强导致产品矩阵的深度减少1.例如 PPR在PPG结束时以16个操作数开始,对后者不加延迟的惩罚。
2)特殊的4-in-1 SMSD加法器与TCSD求和:为了避免SMSD IPPs的挑战加法,我们设计了一种表示2和的新型无进位加法器[-6,6]SMSD操作数。[-7,7]之间2的补码符号数字(TCSD)格式,其中对所有四个可能的符号组合使用一个统一加法器。
3)改进的TCSD加法:还原过程的其余部分使用特殊的TCSD加法器,这些加法器实际上是快速TCSD加法器的改进版本[5].这种2:1的减小促进了PPR电路的VLSI规律,特别是对于n=16(即IEEE 754-2008(12)的推荐操作数)。
4)最后一次PPR级将最终冗余转换为非冗余级:最后一次PPR级别通常会导致TCSD产品的转换,而后者应转换为BCD。然而,为了提高速度和降低成本,我们设计了一种特殊的混合十进制加法器,具有两个TCSD输入和一个BCD输出。
本文件的其余部分如下组织。在第二部分中,作为背景覆盖,我们简要研究了先前的相关工作,并讨论了相应的IPP编码和还原单元。关于所提出的乘法器,在部分IN中讨论乘法器Y的数字的SMSD记录和预计算的Xmu;L-TPLE、它的PPR和最终乘积计算。分析和合成结果见第四节,其中也提供了性能比较:与最佳前一工程的比较。结论见第五节。
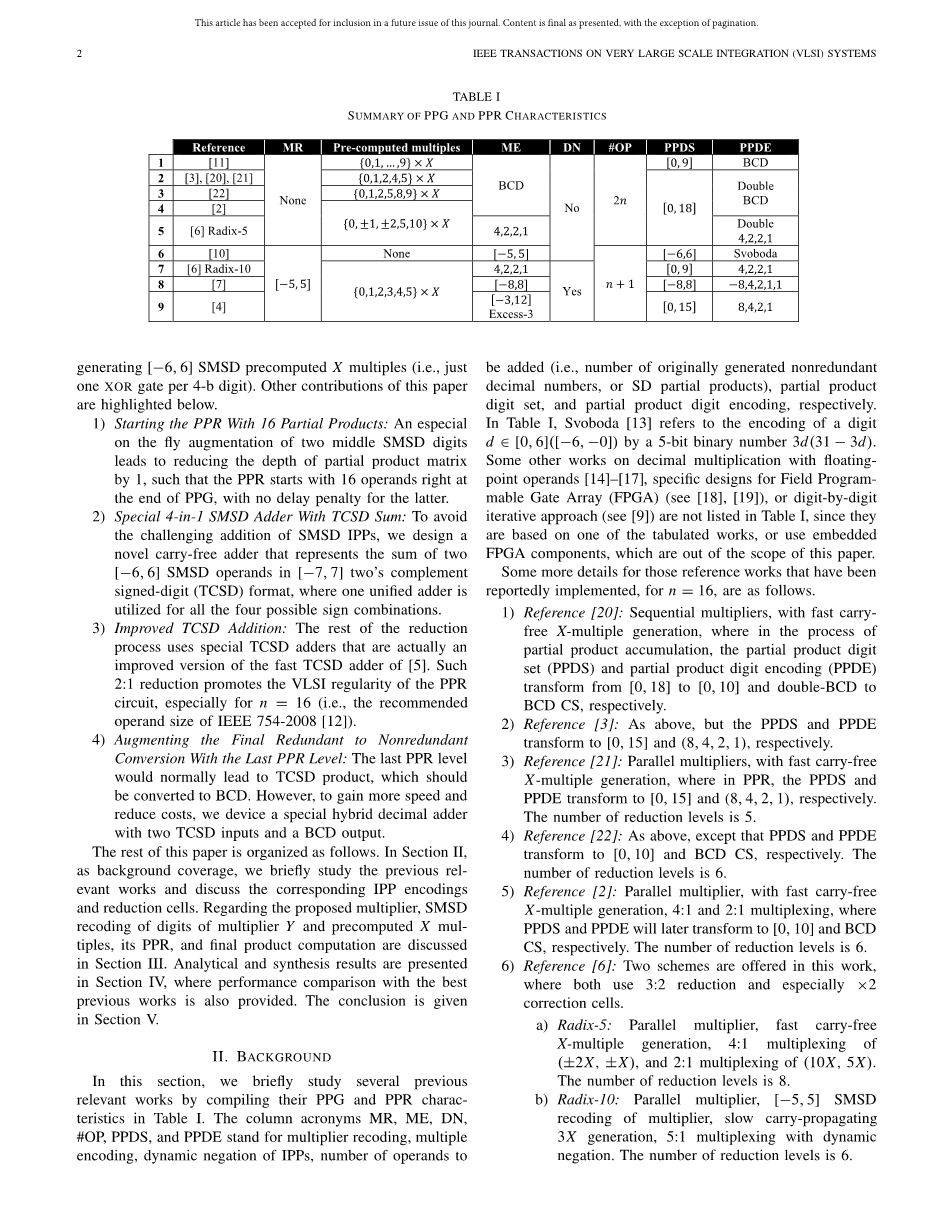
表一
二 背景
这部分中,通过对表一中PPG和PPR特征的整理,简要研究了以往的几项相关工作。列首字母MR、ME、DN、#OP、PPDS和PPDE表示乘数编码、多重编码、IPP的动态否定、操作数到被添加(即一些原本产生的冗余位十进制数,或只部分产品),部分产品的数字集,和部分产品的数字编码。在表一中,斯沃博达[13]是指一个数字([-0,-6])由5位二进制数三维(31-3d)表示。其他一些作品在小数乘法与流动点数[14]-[17],现场程序的具体设计,梅布尔门阵列(FPGA)(见[18],[19]),或数字的位数迭代方法(见[9])未列入表,因为他们是基于一个表的作品,或使用FPGA嵌入式组件,这是超出了本文的范围。
据报道,在n=16的情况下,这些参考作品的更多细节如下。
1)参考[20]:序列乘子,具有快速无载X-多代,其中在部分乘积积累过程中,部分乘积数字集(Ppd)和部分乘积数字编码(Ppde)从[0,18]至[0,10]和双-BCD 到BCD CS。
2)参考[3]:如上所述,但PPDS和PPDE分别转换为[0,15]和(8,4,2,1)。
3)参考[21]:并行乘法器,快速进行免费X-多代,在PPR,劳动防护用品和PPDE分别变换[0,15]和(8,4,2,1)。减少的数量是5个。
4)参考[22]:如上所述,除了PPDS和PPDE分别转换为[0,10]和BCD CS。减少的次数为6。
5)参考[2]:并行乘法器,快速无载X-多代,4:1和2:1多路复用,PPDS和PPDE将随后分别转换为[0,10]和BCD CS。减少的次数为6。
6)参考[6]:本工作提供了两种方案,两种方案都使用3:2的减少,特别是x2校正单元。
a) 基-5:并行乘法器,快速无载X-多代,4:1复用(2X,X),2:1复用(10倍,5倍)。减少数为8。
b)基数-10:并行乘数,[-5,5]SMSD乘法器编码,慢进位传播3X产生,5:1复用与动态负。减少的次数为6。
7)参考[10]:顺序乘数,慢PPG通过BCD-to-[-5,5]对乘法器和乘法器的数字进行SMSd编码,然后再逐位复调,直到[-6,6]PPDS通过Svoboda加法器[13]缓慢积累部分产物的PPDS。
8)参考[7]:并行乘数[-5,5]SMSD通过3X、5:1的动态负复用倍数的冗余表示,实现乘法器的快速无载流子X-多产生。约分两个阶段完成。一个是17:8,包括三个等级的CS加法器和一个4-b加法器.。另一个(即8:2)使用两个级别的(4;2)压缩机和一个5-b加法器.。这两个阶段最后都有一些修正逻辑。
9)参考[4]:如上所述,除减少外,IPP为[0,15]基数-10。二进制4:2和3:2的削减与适当的十进制更正。
在[4],[6]以及[7]动态否定预先计算出的X倍数,在所选正倍数的每比特上罚一个异或门,可以降低它们的选择代价。这种否定成本被复制n倍并行的ntimes;n乘法。此外,在[6]中插入的n是10的补充和在[7]中是数字二的互补。对面积和节电有负面影响。校正常数也是如此,由于零处理而更复杂的重新编码也是如此。在[4]中[0,15]部分乘积.节省这些费用的一种方法,就像我们在第三节中所做的那样,就是生成带有符号大小格式的SD预计算X倍数。以便将异或门减少到每位数一个(大约节省75%个否定异或门的数目),并消除上述负面影响。然而,除了在一定程度上降低PPG(例如与[6]的基-5实现相比)之外,在PPR中还引入了新的问题,并在下一节对其进行了解释和解决。其中,我们还将IPP矩阵的深度减小到n=16,有效地在终止PPG之前。
- 十进制指数位表示的十进制IPP。
()通常用最小4-b有符号的数字编码.。例如,考虑在[10]中和在[23]中 分别用符号大小和两个补语表示。后者适用于基本的算术运算,但否定除外,这是最好的符号大小格式。
在本节中,我们提出了一种十进制乘法方案,其特点如下,与表一所列的设计相同:
- [-5,5]短信编码乘法器的数字;
2){0,1,2,3,4,5}X预先计算的倍数;
3)[-6,6]4-b SMSD预先计算倍数编码;
4)每个数字只有一个异或倍数动态否定(即每4bit);
5)n(而不是)操作数被加为ntimes;n的多重化;
6)统一的加法器的所有四个输入符号的组合;
7)[-7,7] TCSD表示累积部分产品;
8)冗余以BCD码转换早开始;
9)最后PPR水平增加最终转换为BCD码。
图1
图1描绘了提议的16x16乘法的一般结构;稍后将解释每个构建块的细节。特别是,在前三个块中,乘法器的数字被重新编码为n个热位。[-5,5]SMSD(即一个符号和5个震级位),增加一个10n加权进位。倍数是预先计算为n的[-6,6]SMSD和10n加权[-5,4]SMSd.每个SMSD包含一个符号位s和3-b震级.。负倍数[1,5](-X)是通过多次动态符号反演得到的。[1,5]X,每数字只需一个异或门。
A 对乘法器的数字进行记录
要求乘法器的原始BCD数字[0,9]X前馈倍数,其中包括硬倍数{3,6,7,9}X,与{2,4,5,8}X不同的是,没有进位传播是不可导的。另一方面,bcd-冗余[-5,5]对乘法器数字的SMSD重新编码加上IPP的动态否定,将所需的X倍数降至只包含一个硬倍数(即3X)的[0,5]X。然而,这种重新编码产生一个进位作为乘法器的(N1)位数,这会使IPP的数目增加1。对于n=16(即建议的IEEE754-2008十进制操作数[12]字大小),这一点尤其不可取。原因是它可能会使2:1的PPR水平增加1,这是可以避免的,这将在第三-C节中处理。
输入输出表达式为(1),其中,表示bcd乘法器的两个连续数字,表示,是目标代码的符号,是目标代码的符号一个热信号,对应于编码乘法器的数字(即1-5)的绝对值,其十进制权等于易的绝对值。更详细的派生信息可在[4],[6],[7],以及[10]中找到。
B预先计算的倍数
我们需要生成{0,1,2,3,4,5},其中X是BCD乘数。唯一的硬倍数3X可以以无进位的方式生成,如果它是通过一个冗余的数字集[5],[7]来表示的。因此,为了PPR的均匀性,我们在同一个SD数字系统中删除了所有所需的倍数。
和表示X,和的两个连续BCD位,其中,,,,,(例如,导致,,,)在,的情况下(在后一个例子中),基于下面的方程式,我们将两位数的BCD数字 重新编码为 , 编码为,这导致 , 和,:
例如,以上的每个新值(即)是,,,
图2
图3
图2描述了上述编码的源、中间和目标位的加权组织,其中。很容易验证,类似的编码可以应用于用相同的数字集表示的其他倍数([-6,6]SMSD)。
可以用BCD位数a(位置i)和b(位置i-l)的比特推导出乘法和X(例如LX(u)、2X(d)、3X(t)、4X(q)和5X(p))的SMSd倍数的相应逻辑表达式。例如3X(t)的逻辑表达式由(3)给出,其余的可在附录中找到。请注意,这种倍数最多有一个额外的数字(即总共68位),因为生成的倍数中最重要的数字最多为4(由于59=45),在BCD到SMSD的转换中仍保留4。
- 部分产品的生成
图3描述了PPG,与正常组织进行这样的为n=4的乘法。剔棒代表BCD位被乘数。IPP矩阵的最深列的深度(即-加权位置)是(n 1),所有的数字都属于[-6,6],除了顶部和底部的列(灰色)分别属于[-5,4]和[-6,3]。
我们将矩阵深度减小到n(例如, ,n=4,和,n=16),在PPG的终止和PPR的开始之间没有延迟。下面是它的工作原理:我们计算两个灰色数字的和(见图3),独立于(并与)正常的PPG并行,如下所示。如果时,编码乘数的-加权进位值为0,则下灰度数字必须为零。因此,不需要增加。对于,设H表示的最有效位数(例如图3中的最高
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[465741],资料为PDF文档或Word文档,PDF文档可免费转换为Word


