
英语原文共 21 页,剩余内容已隐藏,支付完成后下载完整资料
双向板:受力性能、分析和设计
13-1介绍
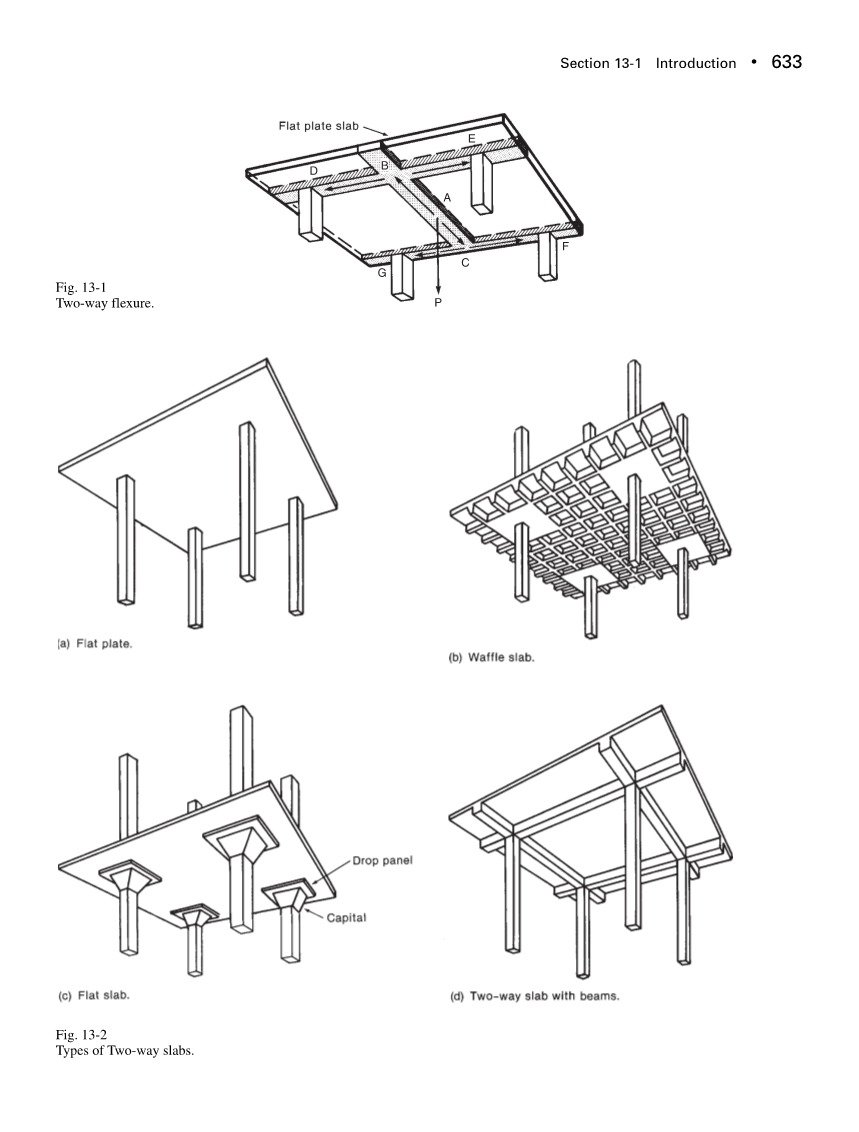
在第十章设计的结构体系中,涉及到了单向板将荷载传递给梁、再由梁传递给柱的内容,如图4-1所示。如果这些梁被纳入板的自身厚度内,体系如图13-1所示。此时,这块板承受两个方向的力。在A点的荷载可以看做荷载沿着板的一边从A传递到B和C,再从B传到D和E,板的另一边传力情况同上。因为这种板必须沿两个方向传力,因此它被叫做“双向板”。
双向板是主要结构材料钢筋混凝土结构中的一种形式。它是一种高效、经济并且广泛使用的结构体系。在实际应用中,双向板有多样的形式。对于相对较轻的荷载,在公寓和小型建筑上按经验采用平板类结构。如图13-2a所示,平板结构就是一块等厚的板简单地支撑在柱上。在一栋公寓楼中,板的上部覆盖面层,板的下部将会作为下面一层的天花板。平板结构在板跨为15-20英尺时最为经济。
对于更大的跨度,竖向荷载传递到柱产生的剪力要求的厚度超过了满足抗弯要求的厚度。因此,在板中部的混凝土并没有得到充分利用。为了减轻板重,缩小构件尺寸并节省材料,在中跨的板可以被交叉的肋取代,如图13-2b所示。同时,在柱附近的区域,为保证剪力在板和柱之间的传递,板的厚度必须充分保留。这种类型的板被称做“格板”(或是双向托梁体系),由玻璃纤维或金属顶盖组成。格板被应用于在板跨为25-40英尺时。
对于工业荷载,应使用如图13-2c所示的平板体系。在这种情况中,传递到柱的剪力可通过使用托板或扩大柱上端形成柱帽以加厚柱边缘板得到实现。托板通常是在柱边的每个方向上扩大跨度的1/6,在柱边提供额外强度和刚度的同时尽量减少了中跨混凝土用量。托板被用于板承受超过100磅每平方英尺和板跨为20-30英尺的情况。如图13-2c所示的柱帽类型由于其造价原因,因此现在相比于20世纪上半段来说并不多见。楼板体系可以包含部分或全部柱之间的梁。如果楼板大致是正方形的,那么这个结构可以被看作带梁的双向板。(如图13-2d)。
13-2 双向板的历史
在钢筋混凝土发展史上最有趣的部分之一就涉及到双向板。因为在生产出第一块板时,并不清楚板的受力情况,所以许多专利系统都是在半经验设计方法的基础上发展起来的。美国早期有关于板的论文吸引了大量的有趣的讨论,每个专利持有人都试图证明他的理论是正确的而其他的都是错误的。
目前尚不清楚是谁建造了第一个平板。Sozen和Siess在他们对板的历史的精彩回顾中声称,美国第一块真正意义上的板是由C. A. P. Turner 于1906年在明尼阿波利斯市建造的。同年,Maillart在瑞士也建造了一块板。特纳的板被称为“蘑菇板”,因为这些柱子向外延伸至楼板,而且在四个方向上都有钢筋固定(也就是指两个正交方向和对角线)。这些钢筋带从柱子上楼板的顶部一直深入至跨中的底部。有些板的钢筋会弯入柱子,其他的钢筋环绕在柱子周围。(如图13-3)
早期的楼板建造是在设计师承担风险的情况下完成的,设计师经常要在几年前建立一个债券并且需要在使用者接受它们之前经常在板上加荷,特纳的设计是基于由H. T. Eddy进行的分析,它是基于不完全的平板分析理论。在这段时间内,在设计中使用交叉梁进行类比导致了一种错误的感觉,即只有部分荷载被传递到每个方向上,所以静力学在某种程度上并不适用于楼板结构。
在1914年,J. R. Nichols[13-2]使用静力学来计算板的总力矩。这个分析在当前的ACI代码中形成了平板设计的基础,这在本章后面给出了介绍。他论文的第一句话是:“虽然静力学不足以确定钢筋混凝土板的应力,但它确实针对这些应力给出了确定的下限。”Eddy[13-3]抨击了这一观点,他说:“这篇论文的基本错误假设出现在第一句中hellip;hellip;”,Turner[13-3]认为这篇论文“从逻辑、实践或理论角度涉及到可以想象到的各种各样荒谬的最独特的组合”。A. W. Buel[13-3]表示,他“无法在论文中找到一个事实,甚至无法找到一个事实的解释。”相反,他觉得这“与事实相矛盾”。Nichols的分析认为当时的平板设计低估了30%到50%的力矩。评审员体现的情绪似乎与他们最喜欢的平板结构设计中表现出来的不足的程度成正比。
虽然Nichols的分析是正确的,并且是在20世纪20年代中期普遍被认为是正确的,但是直到1971年,ACI代码才完全认识到它并要求在静力状态下楼板必须设计为承担100%的力矩。
13-3 弯曲作用下板的受力性能
对于弹性状态下破坏的双向板,有四种及以上不同阶段的受力状态:
1.在开裂前,板的受力情况看作弹性板,在短时间荷载作用下,可以用弹性理论分析其变形、应力和应变。
2.在开裂之后屈服之前,板不再有不变的刚度,这是因为开裂的区域比未开裂的区域的抗弯刚度EI低;同时板不再是各向同性的,因为裂纹在两个方向上可能有所不同。尽管这些条件违反了弹性理论中的假定,但测试表明弹性理论仍然能够充分地预测这些构件的受力状态。一般来说,正常的建筑上的板在使用荷载作用下会部分开裂。
3.在更大的弯曲作用下,在一个或多个区域开始出现钢筋混凝土的屈服,随着内力的重新分布,该区域从已经屈服的部分扩展到弹性区域。在图13-4中展示了一个四边固定的板的屈服过程。在这种情况下,最初的屈服发生在负弯矩区,在长边中心形成局部的塑性铰(图13-4b)。这些铰沿长边开展,最终在板的短边形成新的铰(图13-4c)。与此同时,由于塑性铰在这些板带末端引起的内力重分布,短边方向上板带中部正弯矩不断增加。最终,由于这些板带的正力矩增大构件屈服,如图13-4c所示。在进一步的荷载作用下,屈服区域的边缘线,被称为屈服线,将板材分成一系列梯形或三角形的弹性板,如图13-4d所示。这一阶段的受力状态对应的荷载可以通过使用屈服线分析来估计,这在第14章中讨论过。
4.虽然屈服线将板材分割成一个塑性机构,但由于挠度增加,塑性铰的开展受到阻碍,而板此时形成一个非常平的压缩拱,如图13-5所示。这种情况需假设周围的结构刚度足够大,可以为拱提供反力。这一阶段的受力状态通常不在设计中考虑。
通过对受力状态的回顾可以得到,首先,当荷载超过使用载时,板的弹性理论开始失去准确性,其次,一旦开始屈服,就会发生大量的内力重分配。在这里,我们考虑了一个由刚性梁或墙支撑的板。如图13-2a所示,在孤立柱上支撑的平板的例子中,可以观察到类似的行为,但第一个裂缝会出现在柱的顶部,接着会发生在柱之间的板底部开裂。
在板的弯曲破坏是韧性破坏的。板,尤其是平板,也可能表现出脆性剪切破坏模式。第13-10节和13-11节讨论了双向板的剪切受力状态和强度。
13-4 双向板的力矩分析
图13-6展示了简支梁支撑的简支板。板受荷qlb /ftsup2;。在A-A部分每英尺宽的木板的弯矩是:
板整个宽度的总力矩是:
(13-1)
对于求跨度为l1宽度为l2的简支板的最大力矩来说,这是一个熟悉的方程。
板在每根梁上施加均匀的荷载ql1/2ft。因此,在B-B部分的梁的弯矩是:
各梁的弯矩总和是:
(13-2)
重要的是要注意到,整个荷载在板上的传递方向都是东西方向,在板上引起了大小为wl1sup2;的弯矩,其中w=qlsup2;。之后所有的荷载被横梁沿南北向传递,在梁上引起了相似的弯矩。在图13-7所示的双向板上也发生了同样的事情。A-A和B-B部分所需的总力矩为:
(13-1)
和
(13-2)
再一次,荷载沿东西向传递,之后荷载再沿南北向传递——这一次荷载贯通两个方向。当然,无论结构是否具有单向的板、梁、双向板或是其他结构,这都是正确的。
Nichols对板弯矩的分析
该分析用于推导由Nichols[13-2]在1914年提出的等式(13-1)和(13-2)。Nichols的原始分析是在圆柱上的板给出的,而不是在推导等式(13-1)和(13-2)时所假设的支座。由于矩形柱在如今更常见,因此之后的推导考虑了这个情况。假设:
- 在一个巨大的结构中的嵌板是典型的矩形板
- 结构中的所有板都具有相同的负载。
这两个假设是为了确保力矩包络线和剪力矩和扭转力矩等于零的线,在结构中是对称的线。这样就可以将图13-8a中显示阴影部分的部分隔离开来。这部分是受对称线限制的。
对竖向荷载的反应是通过板面的剪力来传递给柱的。我们必须知道,或者假设,这个剪力的分布来计算板的弯矩。最大的剪切位移发生在柱角,在柱边的中间部位位移较小。为此,我们将假定:
- 柱的抗力集中在每一根柱的四个角上。
图13-8b显示了受力和力矩作用的板单元的侧面图。在阴影板的中心施加的荷载是(ql1l2/2),减去柱上所占区域的负荷(qc1c2/2),这是由柱角向上的反力平衡的。
总静力力矩M0,是负弯矩M1,和正弯矩M2的和,由A-A线上弯矩求和计算得出:
以及
(13-3)
ACI代码稍微简化了这个表达式,它用ln替换了方括号中的部分,ln是柱面层间的净跨:
以及
(13-4)
等式(13-3)和(13-4)的比较显示出与等式(13-3)括号中的部分只有轻微的不同,而整个静弯矩的方程可以写成:
(13-5)
对于圆形柱,Nichols假定剪力是均匀分布在柱的表面,得出:
(13-6)
其中,dc是柱的直径或柱帽。Nichols将它近似为
(13-7)
ACI代码使用等式(13-5)表达,其中ln基于与圆柱面积相同的方柱间的的跨度。在这种情况下,。
对于方柱,c1/l1的实际取值大致在0.05到0.15之间。当c1/l1=0.05,且c1=c2时等式(13-3)和(13-5)可简化为,其中K各自取0.900和0.903。当c1/l1=0.15时,K相应的值分别为是0.703和0.723。因此,等式(13-5)近似代表了方柱支撑的板力矩。随着c1/l1的增长,变得越来越保守。
对于圆形柱,dc/l1实际取值范围大致在0.05到0.20之间。当dc/l1=0.05时,等式(13-6)可得K=0.936,同时等式(13-5),ln定义为,可得K=0.913。当dc/l1=0.2时,从等式(13-6)和(13-5)中可得K相应的值分别为是0.748和0.677。因此,对于圆柱来说等式(13-5)比等式(13-6)倾向于低估M0约10%。
如果对图13-8c中所示构件的平衡进行研究,就M0的相似会导致l1和l2互换,c1和c2。这再次表明,总荷载必须满足L1和L2方向的力矩平衡。
13-5 板的力矩分配
板块曲率与力矩之间的关系
第14-1节简要介绍了双向板弹性分析的原理。力矩的基本方程是式(14-6)。通常,在研究混凝土板时,泊松比,nu;,等于零。在这种情况下,式(14-6)简化为:
(13-8)
在这些方程中,表示了在x方向上的板带的曲率,表示了在y方向上的板带的曲率,即板带的曲率为
其中r为曲率半径(从平板的中轴线到平板弯曲时形成的曲线中心的距离),1/r为曲率,y为从向心轴到发生应变的纤维的距离。在弹性弯曲构件中,曲率是
这说明了曲率和力矩之间的直接关系。因此,通过观察板的偏转形状,可以定性地估计力矩的分布。
图13-9a是一个矩形板,用刚性梁固定在四周。画出了一条纵向板带和两条横向板带。这些板带的偏转形状和相应的弯矩图如图13-9b至d所示。当偏转的形状向下凹时,弯矩会导致底部的压缩,即力矩为负。这也可以从式(13-8)中看到。由于z被取为向下为正,正曲率对应于向下凹的曲线。从式(13-8)可得,正曲率对应于一个负弯矩。弯矩的大小与曲率成正比。
最大的挠度,Delta;2,发生在板的中心。因此,它的曲率(即B板带中的弯矩)大于A板带的曲率。C板带的中心部分基本是直的,这表明该区域的大部分载荷都是通过板的短方向单向传递的。
在板上存在的扭矩,mxy,可以用交叉板带的类比来说明。图13-10显示了图13-9所示的板带B的截面图。在这里,板由一系列平行于如图13-9所示的板带C的梁的横截面表示。这些板带在扭矩mxy的作用下一定会发生扭转,如图13-10所示。
以刚梁或墙上支撑的板的弯矩
在一系列正方形和矩形板上的内力分布将会以其中之一为例给出。负弯矩MA,以及正弯矩MB的分布如图13-11a和b所示沿线穿过板带。MA的分布可能显示为连续曲线,如实线围成的阴影区域所示,或者虚线所示的一系列阶梯,其上任意点的高度表示弯矩的大小。在板带A - B - C中弯矩的分布被绘制为如图13-11c或13-9所示。
这些弯矩用Cqb2表示,其中b是短边尺寸。C的值在正方形的简支单向板中是0.125。单位为lb-ft/ft或kN·m/m。在所有的情况下,力矩图都是在均布荷载q作用下的。
图13-12显示了一个简支的正方形板的弯矩图。力矩作用于所示的线就像显示的那样(类似于图13-11a)。板上最大的弯矩是以对角线为轴,如图13-12b所示。
重要的是需要记住,总负荷必须通过板或者梁的
全文共6558字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[12784],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


