英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

2017年第五十五届Allerton会议

Allerton House，美国伊利诺伊州UIUC

2017年10月3日至6日

LDPC 码的停止集消除

Anxiao（Andrew）Jiang，Pulakesh Upadhyaya，Ying Wang，Krishna R. Narayanan，Hongchao Zhou，Jin Sima and Jehoshua Bruck

计算机科学与工程系, 德州农工大学

电子和计算机工程系, 德州农工大学

山东大学信息科学与工程学院

加州理工学院电气工程系

摘要

本文研究停止集消除问题，即给定一个停止集，如何去除最少的删除，以便通过k次迭代（包括k =infin;）中的置信传播来解码剩余的删除。 问题的NP硬度已被证实。 给出k = 1的近似算法。 并且当停止集合形成树时，有效的精确算法被提出用于一般k。

1.导言

在本文中，我们研究了LDPC码的一个基本理论问题：当一个噪声LDPC码字中的擦除不能被解码器纠正时，如何去除最少的擦除，以便剩余的擦除变得可解码？这个问题有几个应用程序：

分布式存储。像HDFS这样的分布式文件系统已被广泛应用于大数据应用。通常，它们将数据存储在块中，并将ECC应用于块（其中每个块被视为ECC的码字符号）。二进制LDPC码当然是分布式存储的有吸引力的候选者，因为它们具有优异的码率，良好的局部性（例如，可以通过本地磁盘从几个相邻块中恢复丢失的块）以及优异的计算简单性（仅使用XOR对于解码，因为当每个块具有t个比特时，解码可被看作并行解码的t个二进制LDPC码）。同时，几乎所有大型IT公司都在不同地点存储多份数据。因此，当一个站点在LDPC代码中丢失了一些块并且无法自行恢复它时，它需要从其他远程站点检索丢失的块。由于与远程站点的通信比访问本地磁盘成本高得多，因此只要剩余的擦除可解码，就希望尽量减少从远程站点检索的块数。

通过反馈进行卫星与地面通信。考虑卫星到地面通信，其中数据（例如，大感测图像）被分割成分组（即，块），并且LDPC码被施加在分组上（类似于分布式存储的情况）。由于信道嘈杂，地面接收的一些数据包可能无法解码，地面将请求卫星重新发送一些丢失的数据包。由于卫星地面通信的成本很高，因此希望最小化重发分组的数量。

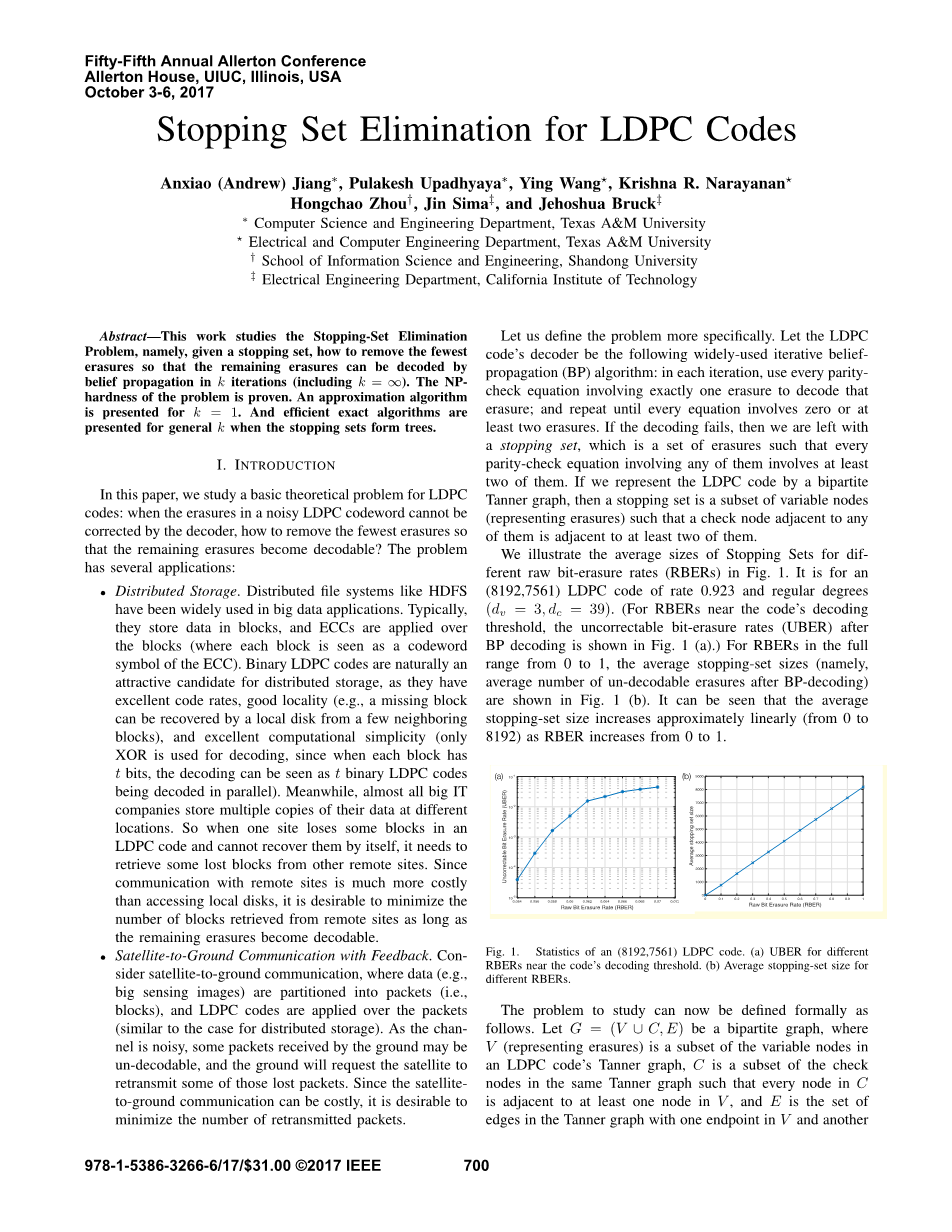
让我们更具体地定义问题。让LDPC码的解码器成为以下广泛使用的迭代信念传播（BP）算法：在每次迭代中，使用每一个只涉及一次擦除的paritycheck方程来解码该擦除;并重复，直到每个方程涉及零或至少两个删除。如果解码失败，那么我们留下一个停止集，这是一组删除，这样每个涉及它们的奇偶校验方程至少涉及其中的两个。如果我们用双向Tanner图来表示LDPC码，则停止集是变量节点的子集（表示删除），使得与其中任何一个相邻的校验节点至少与其中的两个相邻。我们举例说明了图1中不同原始比特擦除率（RBER）的停止集的平均大小。它是针对速率为0.923的（8192,7561）LDPC码和正则度 (d_v = 3, d_c = 39)。（对于接近码的解码阈值的RBER，BP解码后的不可校正的比特擦除率（UBER）如图1（a）所示。）对于从0到1的全部范围内的RBER，平均停止集大小即BP解码后的不可解码擦除的平均数量）如图1（b）所示。可以看出，随着RBER从0增加到1，平均停止集大小近似线性增加（从0到8192）。

图1 (81927561) LDPC 码的统计

(a) 在代码的解码阈值附近为不同的 RBERs (b) 不同 RBERs 的平均停车设置大小

现在可以将学习问题正式地定义如下。假设G =（Vcup;C，E）为二部图，其中V（表示擦除）是LDPC码Tanner图中变量节点的子集，C是同一Tanner图中校验节点的子集， C中的节点与V中的至少一个节点相邻，E是Tanner图中边的集合，其中一个端点在V中，另一个端点在C中。如果C中的每个节点具有二次或更多次数，则称为G停止图和V被称为停止组。现在让kge;1是一个整数参数。如果在G上运行的迭代BP算法（如前所述）可以在k次迭代内对V中的所有变量节点（其中V中的每个变量节点都是擦除）进行解码，那么V被称为可解码集（或简单地可解码）。否则，它是一个不可解码集（或者简单地不可解码）。 （这里我们引入参数k来使问题更一般，并且不仅控制擦除的可解码性，而且还控制解码的时间。）注意，停止集必须是不可解码集，但反之亦然。我们研究的问题称为停止消除（SSEk）问题，如下所示。

定义1.给定一个停止图G =（Vcup;C，E），如何从V中移除最小数量的变量节点，使得其余变量节点可以在k次迭代内通过BP解码来解码？

如果对“k次迭代”的约束不存在，我们可以看到k为infin;并称之为SSEinfin;问题。

本文的其余部分安排如下。 在第二节和第三节中，我们分别证明了SSEinfin;问题的NP-硬度和有限k的SSEk问题。 在第四节中，我们提出了后一个问题的近似算法。 在第五节中，我们提出了有效的算法，当停止集形成树结构时，它为SSE问题返回最优解。 在第六部分，我们提出结论。 由于空间限制，我们跳过一些细节进行证明和分析。 有兴趣的读者可以参考完整论文[3]了解详情。

2.SSEinfin;问题的NP-Hardness

在本节中，我们证明了SSEinfin;问题是NP难题。证明有两个步骤：首先，使用众所周知的集合覆盖问题，我们证明了覆盖几乎所有元素的相关覆盖问题 - 我们称之为伪集合覆盖问题 - 是NP完全的;那么我们将后一个问题归结为SSEinfin;问题。

A.伪集覆盖问题的NP完备性

考虑众所周知的集封面问题。假设让T = {T₁, T₂,···, T_n}是 n 元素的一个宇宙 。让 S₁, S₂,···, S_m 是 T的 子集 ，使得T=U^m_i=1S_i（每个Si被认为覆盖了它的元素）。设kle;m是一个正整数。设置的覆盖问题询问是否存在 k 子集的S_i1 , S_i2, ···, S_ik 使得.T=U^k_j=1S_ij现在, 我们定义一个伪集覆盖问题, 它只在其问题中不同: 它询问是否存在 k 子集 s_i1S_{i 2},···, S_ik 使得.|U^k_j=1S_ij|ge;|T|-1

定理2.伪集覆盖问题是NP-完备的。

伪集合覆盖问题与经典集合覆盖问题密切相关。 为了证明上述定理，请参见[3]。

B.SSEinfin;问题的NP-硬度

我们现在通过使用伪套覆盖问题的减少来证明SSEinfin;问题的NP硬度。 让我们从一些结构开始。

考虑图2（a）所示的二分图。 它由四个变量节点 (s_i,t_j,u_ij和w_ij)和三个校验节点(c¹_i,j,c²_i,j和c³_i,j)。我们通过D_i、j来表示它, 以指示它连接节s_i和节点t_j。我们证明了它在迭代BP 解码的一些基本属性.

图2

(a) 二部图 D_i,j, 它连接变量节点s_i和t _j

(b) 图形 D_ij的符号

(c) 伪集覆盖问题的实例, 其中 T = {T₁, t₂, t₃, t₄, T₅} 和 S₁ = {t₁, t₃, t₄}, S₂ = {t ₁, t₃}, S₃ = {t ₂, t₄, t₅}

(d) 相应的图形 G_I

(e) 对应的图形 G_I , 并提供了完整的详细信息

(f) 相应的图形 GII

引理3. 在图形 D_{i j,} 包含变量节点s_i ,t_j ,u_{i, j} ,和 w_{i ,j}作为停止集, 如果变量节点的值 s_i 已知, BP 解码算法将恢复所有其余三个变量节点的值.

另一方面, 如果变量节点的值 t _j 已知, BP 解码算法将无法恢复其他三个变量节点的值.

证明: 如果值 s _i 通过使用检查节点来了解 c ¹ _i、j 和 c ² _i、j , BP 解码算法将恢复u _{i, j} 和 w _{i, j} 的值。然后通过检查节点 c³_{i, j}, 它将恢复 t _j 的值.

如果值 t _j 变为已知, 因为 c ³ _{i, j} 次数为3, BP 算法将无法恢复任何其他值。

图形 D_i、j 将被视为连接节点s _i 和节点 t _j 的'小工具' 。为了简化演示文稿, 在下面, 我们通常用图 2 (b) 中所示的符号来表示它, 其中 '门' g _{i, j} 代表 五节点 (c ¹ _i、j , c ² _i、j , c ³ _i、j , u _{i, j} , w _{i, j} ) 及其事件边缘。门的 '方向' g _{i, j} 表示上述引理中显示的 '定向' 属性: 解码 s _i 导致解码 t _j , 但不反之亦然.

如前所述，考虑输入参数的伪集覆盖问题 T = {t₁, t₂,···, t_n}, S ₁ , S ₂ , ···, S_m 和 k le; m 。为了将其减少到 SSEinfin; 问题, 我们将伪集覆盖问题的每个实例映射到 SSEinfin;问题的某个实例.

让我们从生成二进图G _I开始。我们首先分配m n个节点：对于伪集覆盖问题中的每个子集S _i（1le;ile;m）或元素t _j（1le;jle;n），在G _I中存在对应的变量节点s _i或t _j。 然后，每当伪集覆盖问题有t _jisin;S _i，我们通过二部图D _i,j连接节点s _i和t _j。 这样获得的图形是G _I.下面显示了一个示例.

示例4。让伪集覆盖问题为 T = {T₁, t₂, t₃, t₄, T₅} 和 S ₁ = {t₁, t₃, t₄}, S₂ {t₁, t ₃}, S₃ = {t₂, t₄, t₅}。(因为 k 与映射无关, 我们不指定它。) 如图2（c）所示，当且仅当t_jisin;S_i时，存在Si与tj之间的边。在图2（d）和（e）中都示出了相应的图G_I， 在图 2 (d) 中使用每个 d_i、j 的符号, 以及的完整详细信息. G_I 如图 2 (e) 所示。很容易看到 G_I 和伪集覆盖问题之间的对应关系。

我们现在创建二进图 G_II 如下所示。给定的图形 G_I, 我们添加 m 1 附加检查节点c₀, c ₁ , c₂,···, c_m 。对于 0 le; i le; m 和 1 le;jle;

全文共17196字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[12725]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

您可能感兴趣的文章

• 看边界：边界感知面部对齐算外文翻译资料
• 看边界：边界感知面部对齐算外文翻译资料
• 一种支持分布式正态智能监控的多代理体系结构外文翻译资料
• 增强的无线局域网协作MAC外文翻译资料
• 近眼显示器的绝对辐射和光度测量外文翻译资料
• 红外遥控系统外文翻译资料
• 一幅单一图像中雨滴去除的专注生成对抗性网络外文翻译资料
• 深度残差学习在图像识别中的应用外文翻译资料
• 低成本，便携式室内环境质量监测装置的设计与开发外文翻译资料
• 使用基于查询蓝牙的RSSI概率分布进行室内定位外文翻译资料