
英语原文共 12 页,剩余内容已隐藏,支付完成后下载完整资料
非轴向应力下埋置型光纤光栅传感器应力应变传递机理分析
摘要
当FBG传感器被埋置于结构中测量应变时,部分应变会被传感器的保护层吸收。如果FBG传感器的轴向与被测材料外主应力方向间有一偏角,那么被测材料与传感器之间的应力应变传递效率,跟两者平行时的应力应变传递效率相比,就要高一点。为了评价非轴向应力下一段光纤光栅与周围基质间的相互影响,特此建立了合适的应力应变传递模型。为简化数学的严谨化处理,我们引进了一些理想化假设。为描述保护层之间的应力应变损失程度和传递给纤芯层的具体数值,我们同样引进了应力应变传递效率这一概念。据理论成果显示,光纤光栅传感器的偏角对基质向纤芯层之间应力应变传递的过程有很大影响,并且这一结果也在一系列用光纤光栅传感器做的实验后被证实。受传感器定位角偏差的影响,我们也进行了应力应变平均传递效率的误差评估。
关键词:非轴向应力;光纤光栅传感器;应力应变传递;剪滞效应;误差分析。
1绪论
近年来,结构健康监测的研究与发展吸引了众多学者,这也反映了重要的土木工程基础建设,尤其是使用周期长的桥梁和大楼,日益恶化的健康状况。选择合适的传感器测量结构状态是结构健康监测的重要一环。过去的几十年以来,为了测量结构的应力应变,我们已经研发出了多种传感器的分布形式。而其中,光纤光栅传感器相较于其他种类的传感器更有优势,因为它能够埋置于复合材料中全天候勘测结构健康状况。这些在在过去几年中都得到巨大的发展。
与常规传感器相比,光纤光栅传感器有如下的优势:
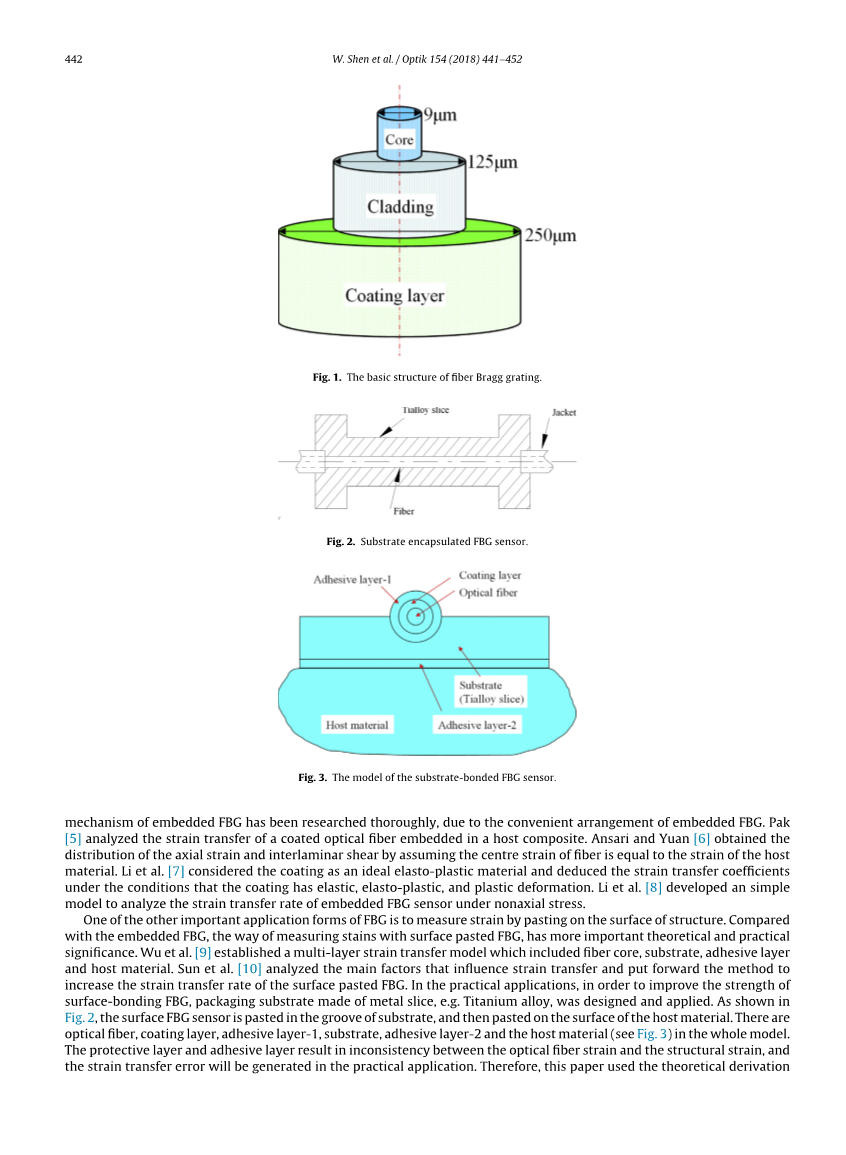
- 体积小:单模光纤的内径一般都为9mu;m。涂覆层,亦即纤芯外层,外径一般为250mu;m,内径一般为125mu;m。
- 精确度高:它的温度精确度为10pm/℃,应变精确度为1.2pm/mu;ε。光纤解调分辨率为1pm。也就是说,温度和应变的精确度分别为0.1℃和0.83mu;ε。
- 抗腐蚀性强:纤芯层的主要成分是二氧化硅。二氧化硅在酸碱性环境中都非常稳定。
- 抗电磁干扰:光纤光栅传感器利用光波传递信号,且光纤不导电。因此,它的信号在电场中不会受干扰,也不会干扰外部电磁力场的分布。
- 应用广泛:即使原理相同,利用不同的分布形式,它可以被用来测量各种物理参数,例如温度、应力、位移、加速度、流量、压力等。而对于传统的传感器,每种传感器都有其独特的原理。
- 易于测量建后难以到达的位置和进行远程监测。
多个不同峰值反射波长的光栅都能被写入同一个光纤中,并且每一个光纤光栅都是独立的传感器。这样的话,光纤光栅传感器就能轻而易举地组成传感网络,让3000多的传感器分布于仅仅4条光纤上的构想也已经实现,而且这已经是一类典型的准分布形式了。自1989年Morey et al首次使用光纤光栅传感器开始,这几十年来光纤光栅传感器已被广泛运用于众多领域当中。在土木工程这一行业里,不仅光纤光栅传感器本身结构有了很大发展,而且在实际应用中像桥梁工程、基础建设、水坝、海底管道等大型复杂结构工程也都有了长足进步。
通过运用全息技术,折射率能在单模光纤内部形成永久周期性调制。FBG的工作原理如下:光纤的任一由形变或温度变化产生的轴向应变都会改变反射光波的波长。如果排除温度所造成的影响,那么通过研究反射波长的变化就可以了解到这一应变的值了。
基于这一原理,布拉格光栅的反射光谱与被测材料的应变之间的关系就成为了确定测量精准度的重中之重。这一问题已经吸引了相关学者的注意,且已有了一些卓有成效的研究成果,研究领域主要被划分为三类。
在实际应用方面,因为光纤的纤芯非常脆弱,所以FBG传感器需要一层保护层来光纤层内部,或者也可以在光纤与被测材料连接处添加粘结层。在选用埋置型FBG传感器时,由于保护层产生剪切形变,周围的材料对光纤纤芯有应力或应变的传递,传感器的形变正是依靠这一传递而产生。在所有因素当中,影响传感器检测材料应力应变分布的精确与否,很大程度上取决于保护层材料的特性。因此,被测材料的应力应变与保护层的应力应变之间的联系是了解结构状况的关键所在。先前已有很多有关埋置型光纤光栅传感器测量各向同性材料的建模分析。由于要将荷载施加于被测材料系统的原因,这些模型的目的都是计算光纤本身的应变,加强传感器的灵敏度。为解决预埋光纤的混合物结构计算光纤应变传递的难题,Cox et al在1951年率先发表了剪滞理论,这一理论的发表也成为预埋光纤型混合结构和其他相关领域最为重要的理论基础。Nanni et al探讨了光纤光栅传感器与混凝土之间应力应变的传递关系,并以此来用光纤光栅传感器测量混凝土的应变。Pak 分析了含有涂覆层的埋置型FBG的应变传递,由平行于光纤的远源纵向切应力向被测材料施压。在这种情况下,当其弹性模量为材料弹性模量和光纤弹性模量的几何平均值时,保护层就能传递其最大剪切应变。Ansari和Libo建立了检验被测材料与埋置后光纤之间相互影响的简易模型,该模型基于光纤和材料的应变在传感器测量长度的中心保持一致的假设,他们所做的实验都使用白光光纤干涉仪来验证理论结果。Li et al则认为涂覆层是理想的弹塑性材料,并且在弹性形变、塑性形变和弹塑性形变不同条件下可以推断出应变传递效率,这一理论成果已由实验研究证实。Li、Zhou和Ou推导出基于保护层的线性粘弹性本构关系的多界面应变传递机制的一般表达式,且得到了FBG传感器的误差修正方程,提出其顺态和稳态的响应,进而提出提出了弹性和粘弹性相一致的原则,用以解决保护层应变传递线性粘弹性这一类问题。Li将光纤应变转化率假定与传感器测量长度中心部位的被测材料相同,优化了Ansaris的应变传递模型的信息反馈,并推导出更合适的理论传递效率,拓展了多层结构埋置型光纤光栅传感器的理论研究。Zhao、Bao和Chen用由3种包层材料(高分子聚合物、毛细钢、毛细铜)包裹的FBG传感器完成了一系列的实验,并且其半径也全都不同。实验结果显示,通过选择合适弹性模量的包层材料和传感器尺寸可以得到最大剪切应力传递效率。
另一方面,我们也对光纤光栅的频谱响应有个清晰的理解,即对结构施加荷载是其性能的关键。在考虑到这一问题后,光纤机械应力和分布于光纤横截面的折射率都会因为被测材料应变而改变。Tu et al. 着重分析了基于双模理论的FBG传感器的横向应变。由于横向应变和轴向应变对基于理论分析的波长转换有不同的作用原理,所以我们可以从布拉格反射波长的变化中得到三维的应变情况。Prabhugoud,Gill和Peters等推导出了修改过的转置矩阵表达式,计算了当FBG传感器受到高度非均匀应变场的影响时布拉格光栅的反射光谱。研究结果表明,该方法能有效地解决多段耦合模型的求解问题,并通过仿真验证了该方法的有效性。此外,他们还介绍了改进的转置矩阵模型在布拉格光栅传感器上的应用,包括通过遗传算法对光栅光谱进行反演。他们还提出了一种集成的公式作为施加于被测结构的荷载函数,用于计算嵌入在被测材料系统中的光纤光栅传感器的光谱响应,采用两步有限元法对横截面的光学、几何和材料特性进行了建模,计算了光纤传输常量。该方法提供了评估高应变梯度对某些荷载施加的影响的可能性。
同时,粘结式FBG传感器也被广泛运用。研究人员还对表面粘结传感器的应变传递分析进行了研究。在连接到一个结构之前,电子应变计通常被粘在一个垫片上,而在FBG应用的文献中也有类似的想法。Li、Wu和Liu联手设计了一种新型粘结式FBG传感器结构,通过各种实验计算了传感器和被测材料的应变传递效率。尽管设计时有必要使从结构传输到传感光纤的应变能得到最小的减少。将FBG传感器连接到结构上,而不是直接安装一个裸光纤,该贴片仍不失为提供了一种更简单、更结实的方法。Li、Zhou和Ou等人从理论上分析了粘结式FBG应变传感器的保护层应变传递机理并进行误差修正。这一构想为以下研究提供理论基础。Betz et al. 通过有限元分析和实验,分析了从被测材料到FBG传感器的应变传递。实验结果略优于理论预测值,利用他设计的特殊温度补偿,作者描述了布拉格光栅的开花式结构,应变花中每个光栅都有不同的峰值反射波长。
所有现有的应变传递理论都是基于主外应变或应力方向与光纤传感器轴线平行的前提。然而在许多实际情况下,主应变或应力方向与光纤传感器轴线之间存在一个角度。原因如下:
- 当构造非常复杂时,材料主应变或应力的方向不能直接确定,通过实验数据发现,传感器轴并不是在材料主应变或应力方向上的。
- 在实际施工中,有许多施工机械和结构可能非常复杂。如果主应力的方向被控制,传感器就不可能再位于同一方向。
- 埋入式传感器的主要目标是对结构的状态进行长期监测。在其生命周期内,结构所分配的负荷可能发生变化,从而改变主应力的轴线。
- 由于该结构在其使用寿命中受到风荷载和地震荷载等随机载荷的影响。应力轴会随时间变化。
当应变或应力方向与光纤传感器轴线之间存在夹角时,应变传递问题就还没得到解决。在此基础上,我们建立了基于剪滞分析概念的数学模型。该模型由一个圆柱形光纤传感器组成,其周围有一层夹层,其余的物质都认为是均匀的。在分析中,施加载荷的方向与光纤的方向形成了一个角度,而在存在性分析中载荷与光纤传感器平行。在得到了光纤传感器的正常应变光纤传感器表面的界面剪切应力之后,将和的数值计算作为FBG轴坐标位置、方向角和纤芯和保护层的力学性能的函数。在接下来的部分中,我们将对这一工作进行更详细的分析。
2 理论分析
据初始的剪滞分析,我们从以下模型开始分析:光纤光栅传感器被一个由被测材料覆盖的保护层所包围。典型代表体积元如图1所示。通过代表性体积元可以看出,“最小单位”是宏观尺度。
此次分析有以下一些假设:
- 光纤传感器与保护层、保护层与被测材料间的连接都完好无损
- 所有材料都是线弹性材料
- 纤芯与包层材料的不同忽略不计。即指纤芯可被认为是一种单一材料的玻璃纤维。
- 被测材料到光纤、保护层到光纤的应变传递不受外部载荷的直接影响
与此同时,还引用了一下边界条件:
- 在坐标的原点,由于光纤与保护层的变形同时进行所以应变梯度的大小预计是相同的,所以应变梯度大小预计是相同的。
- 在光纤和保护层的末端,应变为0.
作用在光纤微元上的应力dz如图2(a),在大比例Ig/dg的光纤周围,可以认
为剪切应力是均匀的,其中Ig和dg分别表示光纤长度和光纤直径。基于平衡方程我们可以得到以下方程:
, (1)
其中是光纤半径,和分别代表光纤的正应力和光纤表面的切应力,如图2(a)所示。
同样地,在保护层中,保护层平衡方程可以写为:
, (2)
其中表示任一保护层上从到的柱面,表示保护层最大半径,和分别表示保护层表面切应力和正应力。
从代表元素z(如图2(c)所示)方向的整体平衡可以求得以下:
(3)
其中为基质材料的半径,为纤芯轴和基质主应力方向的夹角。
基于剪滞理论的原则,保护层切应力取决于光纤和基质不同的位移,即:
, (4)
其中和分别表示保护层和光纤表面方向上的点位移。通过对方程(4)的z求导,利用应变-位移关系,可以得到以下公式:
(5)
其中和分别为基质和光纤的应变。通过利用基质和光纤中的胡克定律,应力平衡方程可表示为:
, (6)
其中和代表基质和光纤的弹性模量,且表示保护层材料的剪切模量,其中和分别表示弹性模量和泊松比。
将方程(1)-(3)代入(6)中,在光纤表面和周围基质的应力关系中,可以得到以下积分方程:
(7)
简化方程(7),得:
(8)
当光纤传感器嵌入到周围矩阵中时,传感器和矩阵同时变形,其变形的数量级几乎相同。弹性模量的光纤和周围基质至少比保护层大十倍。因此,可以得到以下方程:
(9)
方程(8)可简化为:
(10)
最终和的最终微分方程为:
(11)
其中效率和可以表示为:
(12)
和
(13)
若传感器且,则方程(12)、(13)可表示为:
(14)
(15)
方程(11)结果为:
(16)
从光纤末端应变的边界条件可以确定积分常数A和B的常数。由方程(4)得,光纤末端应变为0:
(17)
亦即,
或 (18)
则A和B为:


