
英语原文共 15 页,剩余内容已隐藏,支付完成后下载完整资料
土工合成材料加筋边坡设计的极限平衡法
By Jorge G. Zornberg,Nicholas Sitar,Members, ASCE, and James K. Mitchell, Honorary Member, ASCE
1摘要:极限平衡法是在土工离心机测试中预测评估加筋边坡模型抵抗失稳的能力。离心试验程序中考虑的变量是筋材间距、筋材抗拉强度和土体抗剪强度。最初进行了大量的测试,以评估在回填材料,土工织物加筋模型,以及在土坡模型的几个接口操作条件下的强度特性。对土工织物抗拉强度、离心模型中单位重量的不均匀性、配筋方向、筋材搭接层、离心机模型侧摩阻力等参数进行了参数研究,并选择了边坡稳定分析方法。所有使用相同回填土的离心土坡模型都产生一个归一化的筋材张力总和。这种归一化值可以解释为土压力系数,它取决于土体摩擦角和坡度。评价还表明,极限平衡应考虑筋材的水平方向应力,对重叠层的稳定提供了重要的贡献,不同的严格极限平衡方法同样提供了良好的结果。实验和极限平衡法得到的失稳水平达到了高度的一致性。实验失稳面和预测失稳面之间的一致性也很好。
2简介
传统的极限平衡法用于分析加筋或无加筋的边坡稳定性。由于对土工合成材料加筋边坡性能的极限平衡预测没有得到充分的验证,对离心机进行了研究,首先评估这些结构设计的假设和参数选择。
以非织造土工织物作为加固单元,建立了一系列加固边坡模型。模型都是1:2坡度并且增加的离心加速度直到发生失稳。模型失稳的特点是通过坡脚良好的剪切面。然而,与在目前的设计认为失稳应该发生在加固土坡的坡脚,在土坡的中部首先失稳的假设相反。实验结果还表明,发生失稳是由于加固体的断裂没有完全,而是由土壤抗剪强度峰值控制而不是临界状态下的抗剪强度(Zornberg等,1998)。
在这些试验观测的基础上,本文的目的是进一步评估离心试验程序的结果,以研究极限平衡法作为土工合成材料加筋土坡设计的依据。在此基础上,对回填土、加筋土工织物和边坡模型中几种界面的强度特性进行了初步评价。然后,在极限平衡分析,对加固边坡不同的假设进行评估,并比较实验结果与极限平衡的预测结果。最后,讨论离心试验结果的标准化及其对土工合成材料加筋土体结构设计的影响。
3离心机的测试程序
所有的加筋边坡模型在本实验测试程序都使用同一坡度(1H:2V)和相同的总高度(254mm)。图1显示了加筋土坡模型中的筋材布置和典型的手段。模型采用砂作回填材料,无纺布作为增强单元。该模型进行逐步增加离心加速度,直到发生失稳。Zornberg等人在1998年详细描述了离心机试验方案的特点。离心机测试可分为三个测试系列(B、D、S)。因此,在这项研究中,每一个加筋边坡模型都使用一个识别测试系列的字母命名,然后是模型中的筋材层数。每个测试系列旨在调查一个变量的影响,如下所示:
bull;基线,B系列:考察筋材垂直间距的影响。本系列离心机模型采用6、9、12、18层增强层。
bull;密集土体,D系列:调查土体剪切强度对土工合成材料加筋边坡稳定的作用。在这一系列的模型建立一个密集的回填砂但与B系列布置相同。
bull;更强的土工布,S系列:考察筋材抗拉强度对边坡性能的影响。在这一系列的模型建立采用比B系列筋材具有更高的抗拉强度但回填密度与B系列相同。
图1.用25.4毫米的筋材间距离心模型[线性电位器(LPS)和线性可变位移传感器(LVDT)]
4材料的性能
对离心模型失稳时影响材料性能的材料和界面强度特性进行适当的评估,以评估极限平衡稳定性分析的预测能力。为此,采用试验方案对回填材料砂土的抗剪强度、用作加固土工织物的抗拉强度和回填与补强界面之间的剪切强度以及回填与离心箱之间的剪切强度进行了评价。这些属性估计在边坡模型中是最有代表性的,准确地预测它们失稳的条件。据此,估算了砂土在平面应变条件下的抗剪强度,并在预设条件下对土工织物的抗拉强度进行了评价。
5回填
在统一的土体分类系统中,采用Monterey No. 30砂,一种干净、均匀级配的砂,建立了模型边坡。颗粒是圆形的到近圆形,主要由石英和少量长石等矿物组成。材料平均粒径为0.4 mm,均匀性系数为1.3,曲率系数约为1.1。砂的最大孔隙比和最小孔隙率分别为0.83和0.53。在边坡模型获得目标的干密度,沙子是通过乾捣法控制砂率和高度。目标相对密度为55和75%的Monterey No. 30砂的单位重量分别为15.64和16.21 kN/m3。
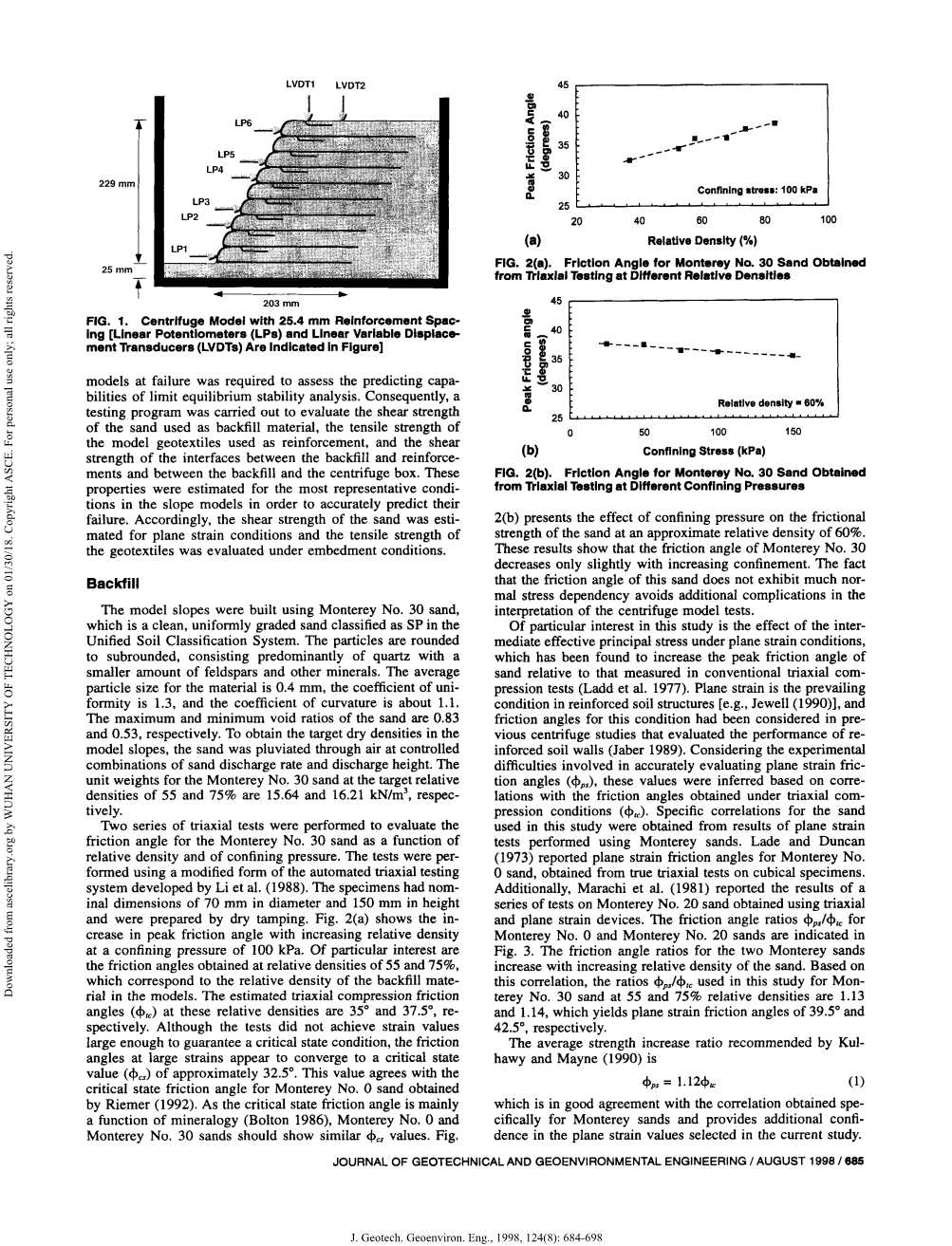
对Monterey No. 30砂的摩擦角进行了两个系列的三轴试验,作为相对密度和围压的作用。这些测试是用李等人在1988年开发的自动三轴测试系统进行的。试样的公称直径为70mm,高度为150mm,用干捣法制备。图2(a)示出了在100KPa的围压下随着相对密度的增加峰值摩擦角的增加。特别是在对应于模型中的回填材料的相对密度55和75%得到的摩擦角。在这些相对密度下,三轴压缩摩擦角分别为35°和37.5°。虽然试验没有达到足够大的应变值来保证临界状态,但大应变的摩擦角似乎收敛到大约32.5°的临界状态值。此值与Riemer在1922年得到的Monterey No. 0砂临界状态摩擦角一致。临界态摩擦角是矿物学中的范畴(Bolton 1986),Monterey No. 0和Monterey No. 30砂应显示类似的值。图2(b)提出了围压对砂的摩擦强度在近似相对密度为60%的影响。结果表明,Monterey No. 30的摩擦角随约束的增加而略有下降。事实上,这种砂的摩擦角没有表现出太多的应力依赖,避免了在解释离心机模型试验中的复杂观点。
在本研究中特别是在平面应变条件下的中间有效主应力的影响,它已被Ladd等人在1990年发现以增加相对于常规三轴压缩试验中测量的峰值摩擦角。平面应变是在加筋土结构中普遍的,对于这种状态的摩擦角在以前的离心机研究中被认为是对加筋土挡墙的性能反映。在准确评价平面应变摩擦角的实验难题中,这些值是基于三轴压缩条件下得到的摩擦角。对本研究中所用砂的特殊关系是从平面应变试验结果获得。Lade和Duncan在1973年报道Monterey No. 0的平面应变摩擦角,从立方体试样真三轴试验得到的。此外,Marachi等人在1981年报道了利用三轴和平面应变装置对 Monterey No. 20号砂进行的一系列试验的结果。Monterey No. 0和Monterey No. 20砂的摩擦角比在图3显示。两种Monterey砂的摩擦角比随着相对密度的增大而增大。基于这种相关性,该值在Monterey No. 30砂中为55和75%,相对密度分别为1.13和1.14,其中平面应变摩擦角分别为39.50和42.5°。
图2蒙特雷30号砂土在不同相对密度下的三轴试验摩擦角 蒙特雷30号砂在不同围压三轴试验得到的摩擦角
图3蒙特雷砂土在平面应变和三轴压缩条件下摩擦角的比值
6极限平衡
极限平衡法(太沙基1956)仍然是最广泛使用的方法来获得复杂的稳定性问题的近似解。无筋结构的极限平衡分析还包括在分析加筋土坡(如破坏面形状)时所需的假设。加筋边坡分析所需的附加假设包括倾斜(例如水平、切向)和沿选定的破裂面(例如,线性,随深度变化)的筋材受力的分布。失稳表面最常用极限平衡分析方法进行边坡包括平面楔,双线性楔面,螺旋,和圆形表面。一些分析方法已经演变成用于确定简单边坡加固要求的表格。
虽然对加固土坡的安全系数有不同的定义,但本定义与土体的抗剪强度有关:
这一定义与传统的极限平衡分析相一致,为非加固边坡分析提供了丰富的经验。
现行的加筋土边坡设计方法通常考虑土相互作用的方法,而不严格考虑(3)中定义的安全系数。这种分析忽略了加固力对潜在破坏面上土体应力的影响,可能导致安全系数与采用更严格的方法计算的因素有很大的不同。各种不同的分析方法已被开发用于分析土工合成材料的加筋边坡。圆弧严格的内部稳定性的方法作为计算机程序编码在本研究中使用的离心机边坡模型的分析。实验离心机的测试结果也与基于其他严格极限平衡法的设计图表所预测的结果进行了比较。
7土工织物抗拉强度的影响
土工织物拉伸试验表明,土工织物抗拉强度高于标准无约束试验强度。虽然由于土工织物机械性能的限制,改进的证据是明显的,但目前的测试程序并没有准确地量化这种改进。另一种方法是通过在本研究中使用的两种土工织物类型的离心模型进行反算来评价原位土工织物的抗拉强度。Zornberg等人在1998年基于在失稳时刻最大应力延深度的分布的推断,当一个恒定的极限拉伸破坏时,以计算为目的的分析提出了。这种计算出来的抗拉强度与破坏时刻的平均张紧力相当。
图4显示计算的安全系数作为土工织物强度和离心加速度的函数。结果表明安全计算因子值伴随筋材强度近似线性的增加。对应的在实验离心机试验获得失稳曲线(n = Nf= 76.5g)。在这个离心加速度,后面计算土工织物强度Tult是和FS值相统一。用土工织物为模型B18加固,后计算土工织物的强度约0.123KN/m这个值作为土抗拉强度模型的极限平衡分析采用土工织物作为增强单元。基于类似的分析采用S9型,估计为土工布抗拉强度为0.184KN/m。
图4.土工织物的强度计算模型B18对安全系数的影响
图5总结了在离心机模型中使用的土工织物抗拉强度的测试程序的结果。图中显示了不同长宽比的土工织物W和土工织物S的抗拉强度。长宽比为2和133(100mm和1.6mm厚度的长度)的结果是从三拉伸试验得到的平均结果。中间结果是从一次试验中获得的。所有试验都是在速度为10mm/min时进行的。图5提供了一系列可能的强度值,可以用于加固边坡模型的分析。如上所述,本文最后选择了一种利用每种土工织物类型建立的离心机边坡的计算结果,得到了最终选定的土工织物强度值。用极限平衡法计算的土体抗拉强度值也在图中表示。反算值与土工织物试验程序的取值范围吻合。
图5.不同试样长宽比下的土工织物模型的拉伸强度
计算的强度值低于使1.5mm规范长度拉伸试验获得的值。两个不同的解释可以表征土工织物的强度性能,对于“实际”对土工织物的抗拉强度:
1.土体强度的实际值是用小长度进行拉伸试验得到的值。从离心机试验的分析得到的较小的强度值可能是由于在分析中假定筋材的分布与深度的分布不一致。
2.土体“实际”强度是在考虑均匀配筋深度分布的离心试验分析中得到的值。由于应变率对试验结果的影响,小距离拉伸试验得到的强度值较高。
虽然在土工织物抗拉强度值最终选择使用两个离心试验的结果,重要注意,这些值不是盲目预测的计算。土工织物拉伸试验程序确定了土的抗拉强度值可能范围,并利用离心试验的结果对这些结果进行了改进。针对低强度非织造布的力学性能难以量化的情况,采用本程序选择其抗拉强度。
8失稳面的实验和预测定位
正确识别潜在破坏面位置对加固结构的设计有影响,因为它影响筋材的长度。所需的锚固长度提供足够的抗拔力来估计超出潜在的破坏面的筋材长度。虽然传统的设计假定潜在失稳表面的位置可以从极限平衡分析来定义,但实验证据证明这种设计过程充其量是有限的。
图6(b)提出的实验和预测模型B18破坏面位置之间的比较。类似的比较从B系列其他的模型,以及从D及S模型系列。图7比较了模型D12和S9。该图显示失稳的位置面,由实验中在土工织物检索测试和记录通过有机玻璃侧壁在测试过程中的图像。总的来说,极限平衡分析预测的临界圆和两种不同的实验结果之间有很好的一致性。
图6(b)土工织物叠合对预测临界圆的影响
图7(a)D12型破坏面的预测和实测位置
图7(b)S9型破坏面的预测和实测位置
失稳面的评估在实验中不同的模型表明,所有离心模型沿着大致相同的破裂面(Zornberg等人。1998)。这一结果也适用于极限平衡分析。图8显示了在本研究模型的分析得到了临界圆的位置,使每个模型的都失稳。总之,实验获得的破裂面与极限平衡预测的所有离心机边坡模型的位置相匹配。利用不同的配筋间距、不同的土体密度和不同抗拉强度的土工织物模型,得到了比较好的离心边坡模型。
图8所有离心机模型极限平衡预测临界圆的位置
9测试结果的规范化
虽然土工合成材料加筋边坡的设计一般都是基于极限平衡法,但特别是在加筋土垂直墙分析中,产生了工作应力设计方法。工作应力设计方法依赖于对土体内部应力状态的假设。具体地,根据土压力系数K定义了潜在破裂面上的水平土应力分布,然后用水平应力和加筋力之间的局部平衡对筋材强度进行常规估计。该系数K的值已被确定为半经验的,在水平回填土和筋材集中加固垂直壁的情况下,它被称作活跃系数Ka,只取决于土体的内摩擦角phi;。
在土工合成材料加筋土边坡中,加固力和水平土应力沿潜在破裂面达到平衡。由此可以推测,潜在破裂面上的水平土应力可用
全文共12689字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[12190],资料为PDF文档或Word文档,PDF文档可免费转换为Word


