
英语原文共 25 页,剩余内容已隐藏,支付完成后下载完整资料
一种新的Signorini的抛物型变分不等式复杂条件下非稳定渗流问题的条件防渗系统
YiFeng Chen,Ran Hu,Chuangbing Zhou,Dianqing Li,Guan Rong
武汉大学水资源与水电工程科学国家重点实验室,武汉430072,中华人民共和国
[摘要]通过将达西定律延伸到自由表面上方的干域并指定边界条件在Signorini类型的潜在渗流表面上,定义偏微分方程(PDE)在整个新兴的领域被制定来用于解决具有自由表面的非稳定渗流问题。然后提出等效于PDE公式的抛物变分不等式(PVI)公式,在PDE公式中Signorini类型的补充条件的通量部分被转化为自然边界条件。因此,渗透点的奇点被消除了,选择试用功能的难度大大降低。通过引入Heaviside函数在有限元分析中的应用,离散值的数值稳定性(PVI)得到很好的保证。建议通过现有的实验室测试进行验证水头的突然上升和下降,然后用于捕捉非稳定渗流在线性下拉过程中,在5条排水隧道的均质矩形坝中的上游水头的流动行为。对地下围岩中的不稳定渗流水水电站工程进一步建模,其中涉及一个复杂的渗流控制系统。与现场监测数据的比较表明,计算结果良好说明蓄水期间的非稳定渗流过程和水库的运行情况以及排水孔阵和排水隧道的防渗效果。版权 2010John Wiley&Sons,Ltd.
2009年11月3日收到; 2010年3月30日修订; 2010年4月8日出版。
[关键词]非稳定渗流;变分不等式;Signorini的状况;自由表面;渗漏控制; 数值模拟
1 前言
长期以来裂隙/多孔介质中的非稳定渗流问题一直被研究,并且它仍然是一个具有挑战性的问题,由于其在性能/安全性方面的重要性而成为岩土力学研究的主题,评估在大坝工程,边坡工程和地下工程等方面进行了比较其稳态对应,理论上由于地下水位的波动非稳定的渗流分析可以描述重力水的运动以及水在媒体中的释放或存储。对比饱和/非饱和渗流分析,一方面,它未能捕捉毛细作用效应和其他运动地下水的形态,避免了保水曲线测定的困难和其他不饱和性质。 因此,非稳定渗流分析仍然广泛适用于工程实践,特别是在对围岩稳定性影响较小不饱和的地下岩石工程中。
不稳定的渗流问题与稳态渗流问题的不同之处在于前者涉及随时间变化的自由表面(或传播前沿),但类似地,它涉及一组的数学中单数的渗透点,导致问题的强非线性。因此,非稳定渗流分析的首要任务是定位自由表面和随着时间的推移渗透点。 为此,在直观的方法[1-4]和文献中提出了不等式方法[5-13],有限元中使用了固定网格配方。
直观的方法包括调整渗透率法[1],残余流量法[2]和初始或虚拟流方法[3,4]等,它们通常涉及启发式迭代程序在每个时间步骤,以确保在干燥领域的流量是可以忽略不计的与湿域相比。 另一方面,变分不等式的方法,在数学上更严格,并且他们总是将传播前沿转化为内在通过定义一个新的初始边界值问题在一个固定的领域[6,10]。
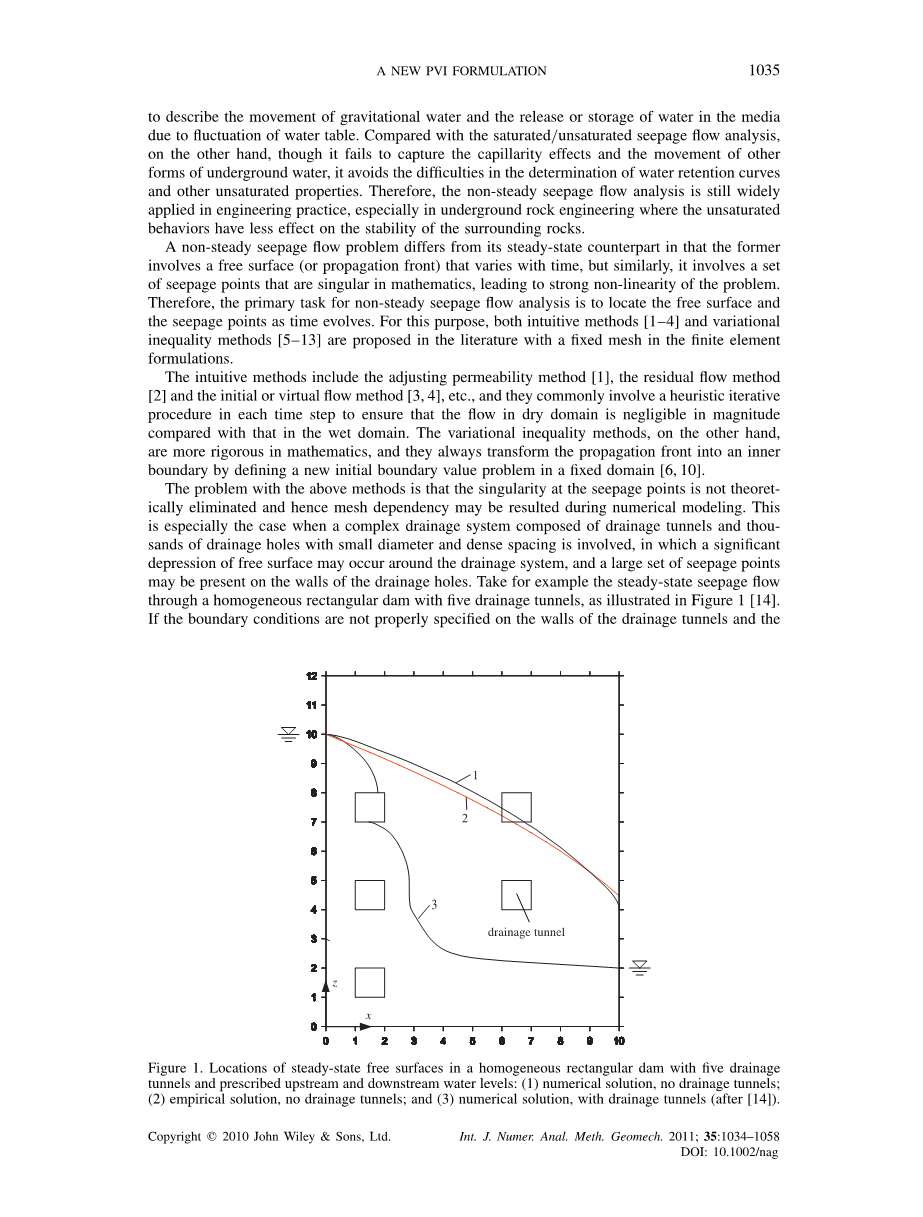
上述方法的问题在于渗流点的奇点不是理论上的消除,因此在数值模拟期间可能导致网格依赖性。尤其是当排水隧道和成千上万的排水系统复杂时涉及小直径和密集间距的排水孔,其中显着排水系统周围可能会出现自由表面凹陷以及大量渗漏点可能存在于排水孔的壁上。以稳态渗流为例:通过一个具有五个排水隧道的均质矩形坝,如图1所示[14]。
如果边界条件没有在排水隧道的墙壁上进行适当的规定,并且图1在具有五种排水的均质矩形坝中的稳态自由表面的位置规定上游和下游水位:(1)数值解,无排水隧道;(2)经验性解决方案,无排水隧道;和(3)数值解,带排水隧道([14]之后),渗漏点处的奇点在问题陈述中没有被克服,即使是这样一个简单的例子,解决方案也是不可为了用减少与大量一维相关的网格生成扩展排水孔,文献中提出了许多建模方法,其中包括等效介质方法[15],子结构技术[16,17],半分析方法[18,19],点井模型[20]和组合元素方法[21]等。然而,现有模型(子结构技术除外)的精确程度或多或少都会失败描述排水孔边界条件的细节,从而折损一些解决方案的理论严格性[14]。
对于稳态渗流问题,作者等人 [22]提出了一个椭圆变分通过将湿域中定义的传统达西定律扩展到不等式的整个新兴的领域并指定潜在渗流表面的边界条件。作为Signorini类型的补充条件, 这个表述理论上消除了渗流处的奇异点有效地克服了由此产生的网格依赖性和数字不稳定性。在此基础上,作者等人[14,23]提出了一种结合这种方法具有的子结构技术和Heaviside函数的变分不等式,已成功应用于解决大坝工程中的复杂排水设施等一些具有挑战性的稳态渗流问题。
通过将我们以前的工作扩展到非稳定渗流问题,在这项研究中提出一种新的抛物线变分方法(PVI)。 PVI公式之间的等价关系并证明了整个域中定义的偏微分方程(PDE)公式,并且建议数值程序用于PVI公式的有限元实现。Signorini类型在势能渗流表面的补充条件的通量部分在PVI公式中转化为自然边界条件,在奇异点处渗透点被消除,数值期间选择试验功能的建模困难明显减少。通过引入Heaviside函数的有限元分析,离散PVI公式的数值稳定性得到很好的保证。所提出的方法通过由Akai等人进行的实验室测试来验证。 [24],并应用捕捉5个均质矩形坝中的非稳定渗流特性排水隧道。在本研究中进一步建模的是非稳定的渗流过程,通过水库蓄水和在地下厂房的围岩作业在中国的水电工程中建立了一个复杂的渗流控制系统。
在这项研究中还显示,上述PVI配方可以平均减少到它对应的水平稳态,即郑的表述[22]。 建立两个几何属性对于自由表面处于减少的稳定状态,这可以作为直观判断是否数值解严格收敛和理论上合理的标准。
本文的其余部分安排如下:第2节在整个域中进行阐述通过达西定律的扩展,PDE形式的自由表面的非稳定渗流问题到干域和Signorini关于潜在渗流边界条件的说明。还介绍了自由表面的稳态渗流问题的几何性质。在第3节中,提出了PVI公式,以及证明PVI和PDE之间的等价关系配方。在第4节中,描述PVI公式的数值实现和验证。第5节介绍了该模型在地下应用发电厂采取了复杂的防渗措施,随后进行总结发言在第6节中介绍。
2 PDE制定非稳态渗流问题
2.1 PDE配方
如图2所示,非稳定渗流区域Omega; 实际上是流经的Omega;w湿区低于自由表面 Gamma;f。 在时间t的湿域Omega;w将被确定只要自由面Gamma;f位于,这事先显然是未知的。 定义一个新的初始边界值问题在整个领域,如PVI公式要求,达西的法律重新定义如下[14,22]:
(1)
其中v是流速,v0是初始流速,k是二阶导水率张量,$ zp /(qwg)是总水头,z是垂直坐标,p是孔隙水压力,qw是水的密度, g重力加速度。 在这里,v0被引入以消除干域Md上的虚流速,其形式为:
(2)
其中H($ - z)是一个Heaviside函数。
(3)
通过引入关于变形固体骨架的材料衍生物的定义:
(4)
渗透整个域的流量则受以下条件的约束连续性方程:
(5)
其中vs是固体骨架的速度,n是介质的孔隙率。假设固体骨架是不可压缩的,则固体骨架的质量守恒,所以有:
(7)
此外,对于不可变形的矩阵,有效应力原理可以表示为:
(8)
delta;和delta;rsquo;分别是总有效应力张量和克罗内克三角洲张量。在没有明确建模媒体的机械响应时,有以下关系可以假定为表征渗流对固体变形的影响:
(9)
考虑到地下水的可压缩性,有:
(10)
delta;和delta;rsquo;分别是总有效应力张量和克罗内克三角洲张量。在没有明确建模媒体的机械响应时,有以下关系可以假定为表征渗流对固体变形的影响:
(11)
其中Gamma;fequiv;{(x,y,z)phi;= z}是自由表面, 等式(10)中的负号是由于等式(3)被定义的事实而引入的在数学原始定义的补充形式中。假定所考虑的介质的骨架由于受到小的变形我们有渗流运动。
假定所考虑的介质的骨架由于受到小的变形我们有渗流运动:
(12)
其中beta;s和εv分别是介质的体积压缩率和体积应变。
将方程(6)和(8) - (11)代入方程(5)得到质量守恒方程的地下不稳定渗流。
(13)
在方程中,第一项考虑了湿域之间的水交换由于地下水位波动造成的干域。 然而,在多孔介质中,在吸液过程中的储水体积分数或在排水过程中的水释放量过程总是少于孔隙率n,这是由于以水的形式保留在孔隙中毛细水和薄膜水。 为了解释这种效应,引力比产量sigma;,在这个术语中会更好,而不是n。 因此,等式可以被重写为:
(14)
连续性方程式受到以下初始条件的限制:
(15)
和以下边界条件:
(1)水头边界条件:
(16)
(2)磁通边界条件:
(17)
其中macr;q是theta;q上的规定通量,n是向外边界单位法向量。对于不可渗透的边界,q = 0。
(3)Signorini型渗流面的边界条件:
(17)
如果我们对方程积分Omega;w和Omega;d分别考虑 Gamma;f作为内部边界并且使用发散定理,则等式可以是等效的以下面的整体形式来表示,考虑到这个事实,重力比产量在垂直方向上移动。
(18)
等式中的第二项实际上表示Rankine-Hugoniot在非稳定渗流的传播前面跳跃条件的通量法线方向涉及不连续,可以表示如下:
(19)
则可以被缩减为以下常规形式:
(20)
因此,在整个域上定义的非稳定渗流问题的PDE公式化可以表述如下:找到一个函数Gamma;(x,y,z; t)在空间中Omega; 并在时间上时域[0,tau;],使得满足方程(20)的PDE,经受初始条件,方程(14)和边界条件方程(15) - (17)和(19)。
从方程(13) - (17)可以证明,如果Gamma;q是一个不可渗透的边界,那么在此期间水头不断上升导致的蓄水过程,Gamma;phi; 只能达到它的上游边界的最大值; 相反,在排放过程中产生的持续下降水头Gamma;phi; 只能在下游达到其最低点边界。
然后,在蓄水期间过程中,有fle;0。结果是,phi;在边界或初始时间达到最大值t0根据抛物型偏微分方程的最大原理,而且,如果phi;达到最大值在时间t的边界上的某个点P处,则根据该强度在P处存在qn(t)gt; 0最大原则(或边界点引理)。 因此,phi;只能在时间t的上游边界达到其最大值。
相反,在放电过程中,有fge;0。结果是,phi;达到最低值根据抛物型偏微分方程的最大值原理,在边界处或初始时刻t0,而且,如果phi; 在时间t的边界上的特定点P处达到其最小值,然后在那里根据边界点引理P是qn(t)lt;0。但是phi; 达不到最低限度初始时间t0由于水头持续下降而降低; 和phi;不能达到最低限度在theta;d上由于qn(t)= 0而导致的不渗透边界上,以及因渗流引起的潜在渗流边界下游边界上的水头比垂直坐标低z(根据等式(17))。因此phi;只能达到其最低限度,边界在时间t。
但是,应该指出的是,如果蓄水和排水,上述特性不会成立过程交替。在这种情况下,f在自由表面的某些部分可能是正的,但是是负的在别人身上,和phi;可能在域内获得最大值或最小值Omega;。
2.2 减少到稳态渗流问题
如果依赖性phi;在t上消失,控制方程,方程(20)和边界条件,方程(15) - (17)和(19),对于非稳定渗流,立即减小至其稳态对应。 受流量和孔隙压力的影响吗Gamma;f用于稳态渗流流动,即qn = 0和p = 0,以下两个几何特性对于自由表面保持稳定:
特性1.任何均质介质中的稳态自由表面必须是连续的光滑。
性能2.任何均质介质中的稳态自由表面不能返回弯曲,除非它与具有不同渗透率的两种介质之间的界面相交。
如图3(a)所示,假设自由表面Gamma;f上存在临界点P,Gamma;f上不存在衍生物。令n1和n2是向外的单位法向量Gamma;f两侧的P,通量条件为Gamma;f,在P处存在-n1·v = -n2·v = 0或v = 0,这与矛盾P开启的事实Gamma;f。 因此1成立。
进一步假设存在上游倾斜媒体接口,例如,联系人界面在混凝土面板和混凝土面板堆石坝(CFR)中的缓冲材料之间如图4所示。假设介质在上游和下游的水力传导率分别为k1和k2。应用接口上任意点的条件相同我们获得了孔隙水压力和流速的法向分量穿过界面的水流的折射定律tantheta;1/ tantheta;2 = k1
全文共18811字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[12021],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


