
英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
基于小波变换的多步骤停车位预测策略
摘要
本文提出了一种结合小波变换(WT),人工神经网络(ANN)和基于可用停车位(APS)变化特征的预测策略的多步骤预测新方法。首先,通过小波变换对几个APS时间序列进行分解和重构。然后,使用人工神经网络,采用以下五种多步预测时间序列预测策略来预测重构时间序列:递归策略,直接策略,多输入多输出(MIMO)策略,DIRMO策略(直接和MIMO策略的组合), 和新提出的递归多输入多输出(RECMO)策略,其是递归和MIMO策略的组合。最后,将预测结果与重建的时间序列相结合产生了最终预测的可用停车位。实验结果看起来是一直支持三个发现。首先,将小波变换应用于多阶段可用停车位预测可以有效提高预测精度。其次,由DIRMO和RECMO策略产生的预测比其他策略更准确。最后,RECMO战略所需的模型训练时间比DIRMO战略少,并且在五种预测策略中所消耗的训练时间最少。
关键词:可用停车位; 多步骤时间序列预测; 小波变换; 预测策略; 递归多输入多输出策略
1介绍
旅客进入繁忙的市中心最大的担忧之一是要知道哪里有可用的停车位(APS)[1]。实时准确预测APS可以提前告知司机哪里可以找到APS。如果APS可以被预先预测得足够久,司机将能够预留停车位并相应地计划路程。 因此,需要可用于更长时间段的可用停车位预测方法,即长期或多步预测,而不是由短期预报方法提供的持续时间。
在长期预测方法的有限现有研究中,刘等人[2]利用递归策略开发了一个加权一阶局部区域方法来预测1小时(12步)的空闲停车位。JI等人[3]提出了一种结合小波神经网络和最大Lyapunov指数法的多步预测模型,并考虑了早期和晚期多步骤APS预测的不同特点,以提高预测的准确性和稳定性。在多步提前时间序列预测领域,已经发现直接策略,多输入多输出(MIMO)策略以及直接策略和MIMO策略的组合(DIRMO)策略也可以用于多步骤预测[4-6]。许多研究比较了不同的多步骤预测策略。ZHANG等[7],SORJAMAA等[8]和HAMZA等[9]认为直接策略优于递归策略在这方面的应用,因为直接策略避免了递归策略中的错误积累。相反,WEIGEND等[10]和BIRATTARI等[11] 都倾向于递归策略优于直接策略,声称直接策略在模型构建期间遭受中间信息损失。关于MIMO策略,KLINE等[12]和CHENG等人[13]认为MIMO策略比递归策略和直接策略的预测性能差。然而,由于MIMO可以保留预测值之间的随机依赖性,因此在BONTEMPI等人[14,15]的研究中,MIMO,递归和直接策略之间的比较,MIMO更优。最后,TAIEB等[16,17]认为,当正确识别控制预测之间依赖程度的参数时,DIRMO策略比直接策略或MIMO策略具有更好的预测结果,因为它提供了保留预测值中随机依赖性的属性与建模过程的灵活性之间的一个权衡。
在这项工作中,提出了多步预测的新策略,它保留了递归和MIMO策略中最吸引人的方面。递归策略使用刚刚预测的值作为预测下一步的输入变量之一,由于随着预测范围的增加而导致错误积累,导致预测准确性越来越差。因此,在理论上和实践中,当迭代值变得更准确时,递归策略的预测性能会提高,可能达到比直接策略更好的精确度水平[18]。由于小波变换可以有效地提高时间序列预测的准确性[18],通过类比DIRMO策略,RECMO策略是递归策略和MIMO策略的结合。同时,通过应用小波变换,改善了在RECMO策略中作为迭代值的MIMO策略输出的准确度。
2改变APS的特征
通过对可用停车位(APS)变化特征的宏观和微观观察,分析其可预测性和随机性,可以更合理地选择训练数据集和预测方法。
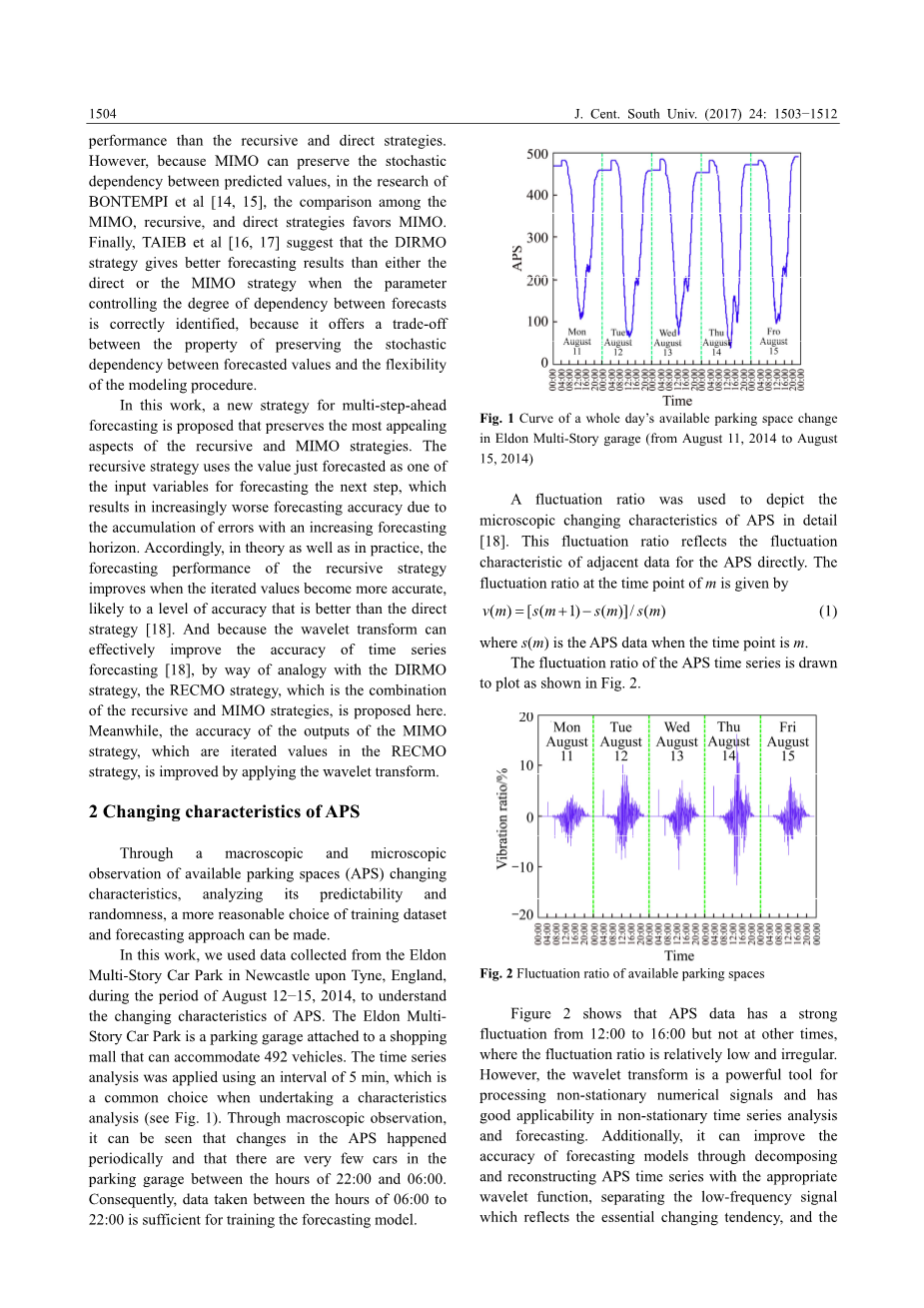
在这项工作中,我们使用了从2014年8月12日至15日期间在英格兰泰恩河畔纽卡斯尔的埃尔登多层停车场收集的数据,以了解APS的变化特征。埃尔登多层停车场是一个连接购物中心的停车场,可容纳492辆车。时间序列分析以每5分钟一次的时间间隔进行,这是进行特性分析时常见的选择(见图1)。 通过宏观观察,可以看到APS的变化周期性地发生,并且在22:00和06:00这段时间停车库中的车辆很少。因此,在06:00至22:00之间采集的数据足以训练预测模型。
图1 埃尔登多层停车场全天可用停车位变化曲线(2014年8月11日至2014年8月15日)
波动率被用来详细描述APS的微观变化特征[18]。 该波动率直接反映APS相邻数据的波动特性。时刻的波动率由下式给出
= (1)
其中是时刻的APS数据。
绘制的APS时间序列的波动率如图2所示。
图2可用停车位的波动率
图2显示APS数据在12:00至16:00之间波动很大,但其他时间段波动率相对较低且不规则。然而,小波变换是处理非平稳数值信号的有效工具,在非平稳时间序列分析和预测中具有很好的适用性。此外,通过用适当的小波函数对APS时间序列进行分解和重构,分离反映本质变化趋势的低频信号与反映不确定因素的高频信号,可以提高预测模型的准确性, 然后将时间序列中的干扰信号屏蔽到高频信号[19,20]。
3方法
图3显示了这项工作提出的预测方法的主要过程。此外,本节介绍了小波变换的基本原理,用于多步骤时间序列预测的策略以及预测模型。
图3预测方法的主要过程
3.1小波变换
小波变换的实现包括两个要素:离散小波变换和连续小波变换。APS时间序列是离散时间序列,这意味着正交二进小波变换适用于APS时间序列的分解和重构。因此,选择Mallat算法进行小波分解和重构。
Mallat算法[21]可以表示为
(2)
其中是低通阶滤波器;是高通阶滤波器,是分解尺度,是原始时间序列。小波分解自动产生金字塔形连续分解结果。因此,可以从Mallet算法获得低频系数矢量和高频系数矢量,,hellip;,。
时间序列样本在用Mallat算法每次进行分解后会减少一半,不适合用于预测。然而,由Mallat算法分解的时间序列可以通过以下方程重建:
, hellip;,0 (3)
其中和分别表示和的双重算子。小波重构可以增加时间序列的样本。 ,,hellip;,和,其样本数与原始时间序列的样本数相同,可以分别在重建,,hellip; ,和后获得,以及重建的时间序列可以表示为 hellip; 。
3.2多步骤时间序列预测的策略
多步骤时间序列预测的一个任务是预测具有N个观测值的历史时间序列[,hellip;,]的下一个H值[,hellip;,],其中gt;1是预测范围。本节将介绍四种现有的预测策略和一种新提出的策略,比较每种预测策略的预测模型的形式和所需数量,并分析其预测特征。
为了便于引入这些策略,必须定义一些符号。这里,和表示过去和未来观测值之间的函数依赖关系;表示用于进行预测的过去值的数量;而是指随机的误差包括干扰,建模误差和噪声。
3.2.1递归策略
递归策略是多步骤时间序列预测的最古老和最直观的策略[22,23],它只训练单个模型来执行单步超前预测,即
,
(4)
当预测范围是步时, 我们从应用模型开始预测第一步。随后,将刚刚预测的值用作输入变量,使用相同的单步超前模型来预测下一步。以这种方式获得预测范围内每个步骤的所有预测值。
如果是训练的单步超前模型,那么预测是按照
(5)
由于时间序列和预测范围内存在噪声,递归策略可能在多步骤预测任务中产生令人不满意的预测结果。随着预测范围的增加而积累的误差是递归策略准确性差的主要原因。过去预测中产生的错误将向前传播,因为这些预测被用作后续预测的输入值。
3.2.2直接策略
直接策略的思想[7,10,11]是独立于其他范围的预测每个范围。换句话说,对于模型,需要从时间序列[,hellip;,]中学习(每个范围需要一个模型),其中
,
and (6)
使用学习的模型获得预测值,如下:
(7)
因此,不使用近似值来计算预测等式。直接策略中的(7),阻止直接策略受到与递归策略相同的错误积累。然而,预测是条件独立的,因为模型是独立学习的。这也对预测准确性有负面影响,因为该策略不考虑变量之间的复杂依赖关系。另外,直接策略需要大量的时间消耗,因为需要学习与范围大小相等的许多模型。
3.2.3 多输入多输出策略
前面描述的递归和直接策略是单输出策略[17],它将数据建模为具有多个输入的单输出函数。
单输出映射建模忽略了未来值之间的随机依赖关系,从而影响了预测的准确性[14,15]。 为了避免这种限制,已经提出了多输入多输出(MIMO)策略。
MIMO策略从时间序列[,hellip;,]中学习一个多输出模型,其中
(8)
:是矢量值函数; 并且是具有不一定对角线的协方差的噪声矢量。
预测将通过多输出模型一步返回,其中
(9)
MIMO策略保留了预测值之间的随机依赖性,从而避免了直接策略的条件独立性以及递归策略的错误积累。由于这些优势,MIMO策略已经成功应用于几个现实世界的多步骤超前时间序列预测任务[14,15]。
然而,MIMO战略预测的所有范围都采用相同的模型结构,从而降低了预测方法的灵活性[16]。为了克服这个缺点,已经提出了一种新的多输出策略,即DIRMO,接下来将介绍这种策略。
3.2.4 DIRMO策略
为了保持直接策略和MIMO策略的优点,DIRMO策略[16]采取中间方法。该策略将范围划分为几个块,然后以MIMO方式预测每个块。因此,步超前预测任务由个多输出预测任务(=)组成,每个输出的大小为。()。
DIRMO策略是直接策略和MIMO策略之间的中间配置,取决于参数的值。当参数的值为1时,DIRMO策略对应于预测任务数等于的直接策略.当参数的值为时,DIRMO策略对应于预测任务数等于1的MIMO策略。
通过调整参数,我们可以通过校准输出的维数来提高MIMO策略的灵活性(在=1的情况下无依赖关系,的最大依赖性)。这提供了保留未来值之间更大程度的随机依赖性和预测器具有更大灵活性之间的有利折衷。
DIRMO策略从时间序列[,hellip;,]中学习个模型,其中
(10)
而:如果1,是一个向量值函数。
预测由个学习模型返回,如下所示:
(11)
3.2.5 RECMO策略
递归策略和直接策略在过去的研究中已经进行了紧密的比拼[7-11],并且DIRMO策略在多步超前时间序列预测领域具有很好的适用性[16,17]。 因此,通过类比DIRMO策略的发展,旨在保留递归策略和MIMO策略中最吸引人的方面,同时通过校准输出的维度来提高MIMO策略的灵活性,这项工作提出了一种新的结合了递归策略和MIMO策略的预测策略,称为RECMO。
RECMO策略的程序如下:首先,我们确定整数参数,它校准输出的维数。对于给定的,RECMO策略的训练集由=组成。在对输出规模为的预测模型进行训练之后,根据递归策略的原则,我们首先通过应用多输出模型来预测第一个步。然后,刚刚预测的值包含在用相同的模型预测下一个步的输入变量中。我们以这种方式继续下去,直到预测整个范围。
在这个策略中,单个模型被训练来执行步超前预测,即
(12)
其中:如果1,是一个向量值函数。
让训练的步超前模型成为。则预测结果由
其中和将值四舍五入到最接近的无穷大整数。在下一节中,RECMO策略将应用于多步超前可用停车位预测问题,以验证其有效性。
总之,已经引入了五种可能的预测策略用于多步骤预测任务:递归,直接,MIMO,DIRMO和RECMO策略。这些策略之间的关系如图4所示。
图4不同预测策略之间的关系
3.3预测模型
每种预测策略要求定义特定的预测模型或学习算法,以便估计表示时间随机相关性的标量值函数或向量值函数。由于这项工作的目标不是比较预测模型,而是多步超前预测策略,为了建立实验,需要选择基础预测模型。在这项工作中,采用了人工神经网络模型,因为它是一种流行的全球学习模型,已被证明在时间序列预测任务中特别有效[24]。
反向传播神经网络(BPNN)是最常见的人工神经网络之一,属于多层前向神经网络的范畴,用误差反向传播算法训练神经网络。这项工作建立了一个三层BPNN模型作为其预测模型,其拓扑结构如图5所示。在这个结构中,输入节点的数量是,隐藏节点的数量是,输出节点的数量是。当等于1时,BPNN是一个标量值函数,但当1时,是一个向量值函数。为了实现BPNN,本文使用MATLAB函数(前馈网络)。
图5反向传播神经网络的拓扑结构
4案例研究
4.1数据描述
2014年8月12日至2014年8月15日以及2014年9月9日至2014年9月12日在Eldon多层停车场收集的数据以及2014年9月9日至9月12日从John Dobson停车场收集的数据被选为案例研究。首先使用5分钟作为时间间隔将数据处理成时间序列。之后,2014年8月12日至2014年8月15日Eldon停车场的数据用于预测试,目的是挖掘最佳参数。接下来,使用2014年9月9日至2014年9月12日从El
全文共14013字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[11994],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


