钻井钻具虚拟仿真系统外文翻译资料

 2022-05-30 22:15:05

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

摘要

钻井操作过程中，过强的粘滑振动会导致钻柱部件过早失效和效率低下。以前的研究工作采用实时测量钻柱的所有状态后反馈给控制器，来抑制这种振动。虽然实时测量在钻柱表面上是很容易实现的，但是只有有限的测量值可以用于井下状态。为了满足井下状态的要求，本文提出利用Kalman估计器来估计井下钻头的位置和速度。在估计器的设计中，非线性的井下摩擦力矩近似为线性的持续扰动模型。然后在估计的状态下应用线性四次-高斯(LQG)控制法法来减少不必要的振动。通过数值模拟法研究该控制方案的性能，采用高保真集总参数模型，考虑了扭转粘滑和横向运动以及非线性摩擦模型。高仿真度模型的动态响应与现场观察到的粘滑振动有密切的一致性。仿真结果表明了Kalman估计器在识别粘滑振动和估计井下摩擦力矩的能力，同时也验证了该控制器在避免粘滑振动方面的有效性。

1.概述

石油和天然气开采的深井用钻柱钻出钻孔。工业油井钻柱的主要部件是顶部旋转机构(旋转台或顶驱)、钻杆和井底钻具组合(BHA)。为了转动钻头，整个钻柱使用顶部旋转机构在表面旋转。将分段钻杆连接在一起，连接顶部旋转机构与底部钻具组合。钻柱动力学具有耦合轴向、横向振动和扭转振动等复杂特性，以及滞回摩擦(Jansen和Steen, 1995;Leine et al.,2002)。非线性摩擦，其特点是低钻头转速下的高摩擦力矩，但在较高的钻头速度下扭矩较小，可以引起粘滑振动(Tjahjowidodo, 2012)。这种粘滑振动发生在钻井深井中，当钻井液与钻头-岩石相互作用摩擦扭矩。突然释放的势能存储在滑动阶段，可以改变底部钻具组合的转速从零到六倍的速度旋转机制,这是通常控制在一个恒定的参考(Jansen和Steen,1995)。从现场测量中举例说明了粘滑振动的实例。这种震动的典型周期为2到15秒(National Oilwell Varco, 2012)。此外，钻柱中严重的扭转振动导致了巨大的离心加速度，使耦合的横向振动引起振动，从而使钻柱撞击井壁(Yigit和Christoforou, 1998)。这些非理想的扭转和横向振动导致过度磨损，过早的工具失效和低的钻速。

需要由主动控制来防止出现这种不需要的振动。为此，提出了各种基于状态空间的控制设计，如最优控制和滑模控制，以减轻钻柱的粘滑振动(AlHiddabi et al.,2003;Zamanian et al.,2007;理查德et al.,2007; Ritto et al.,2009;Yigit Chistoforou,2002)。然而，它们通常需要实时的井下状态测量，而目前大多数的工业监测系统只提供油井表面的实时测量(如顶部旋转机构的转速或表面马达的输入扭矩)(National Oilwell Varco, 2012)。为了解决井下信息不足的问题，本文采用Kalman估计方法，根据陀螺机构的测量结果，对井下状态和井下摩擦力矩进行了估计。通过采用线性连续扰动模型，可以对井下摩擦力矩进行估计，其性质是滞后的。一个线性二次调节器(LQR)被设计用来抑制不需要的振动，同时保持了下孔和顶部旋转机构的期望速度。为了有效地实现，估计器和控制器的设计基于一个简单的纯扭力两个自由度(DOFs)集总参数模型。为了对实际情况下的控制器性能进行评估，本文开发了一种高保真集的钻柱参数模型，模拟了钻柱的特性粘滑振动。该模型由钻弦的纯扭转集参数模型(Jansen, 1991;普埃布拉和Alvarez-Ramirez,2008;Navarro-Lopez和Cortes, 2007a)包括钻铤的扭转和侧向。在井底摩擦的情况下，采用了带条纹曲线的滞后干摩擦公式。从该模型得到的动态响应表明，在粘滑振动方面与现场观测有密切的定性一致。因此，扩展的模型可以代表真正的工厂来验证控制器。论文的其余部分组织如下。在第2节中，描述了耦合扭振和横向振动模型和滞后干摩擦模型。在第3节中提出了抑制非理想钻柱振动的LQG控制策略。第4节讨论了设计的Kalman估计器和LQR在减轻扭转和横向振动方面的模拟性能。最后，第五部分总结全文。

2.钻柱动力学模型

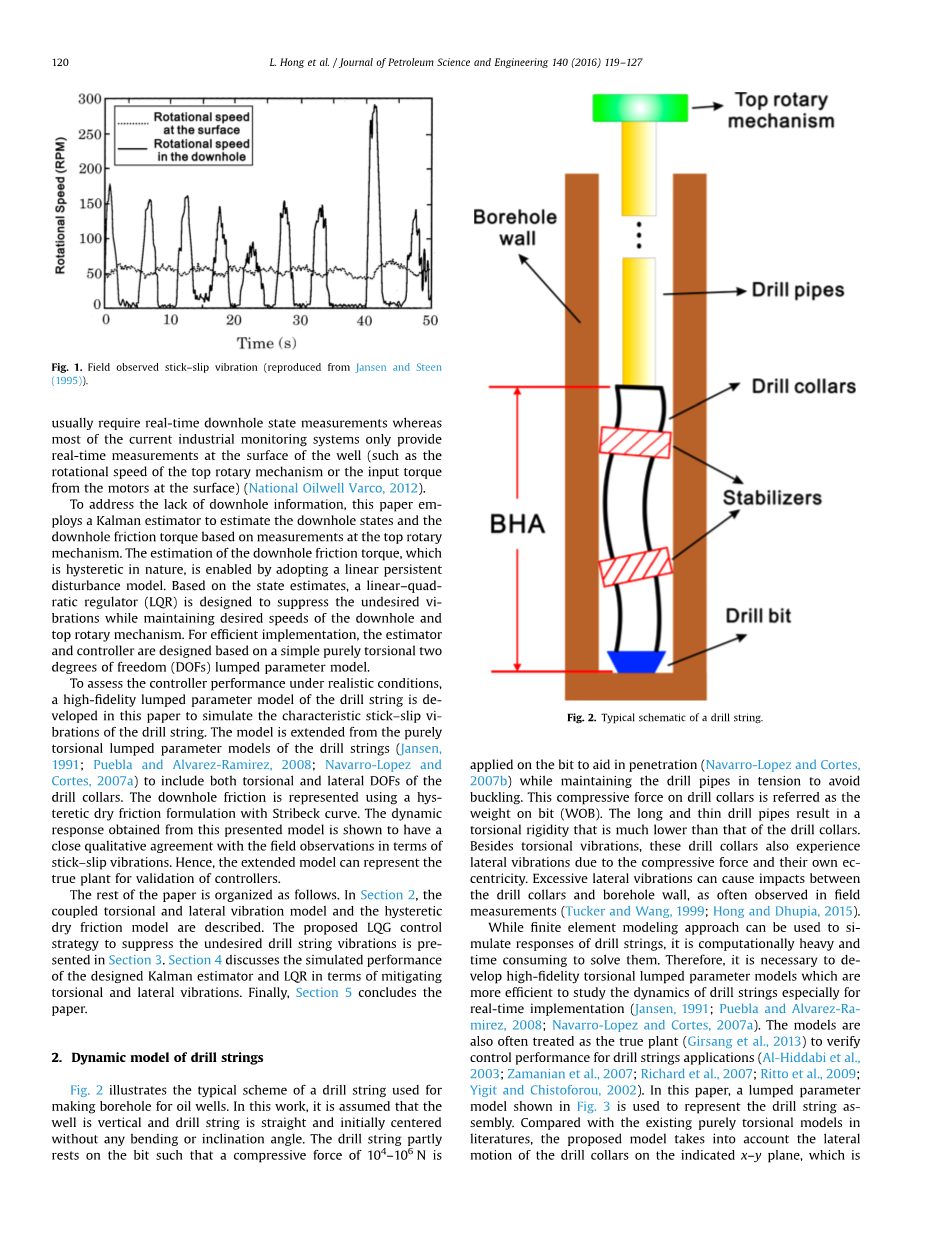
图2阐述了用于油井钻孔的钻柱的典型方案。在这个案例中，假设井是垂直的，钻柱也是直的，最初的中心没有任何弯曲或倾角。钻柱部分依赖于钻头，在钻头上施加104-106 N的压缩力，以帮助穿透(Navarro-Lopez和Cortes, 2007b)，同时保持钻杆的张力以避免屈曲。钻铤的压缩力称为钻头的重量(WOB)。长而细的钻杆产生的扭转刚度远低于钻铤。除了扭转振动，这些钻铤还具有横向振动，由于压缩力和它们自己的偏心。过度的横向振动会引起钻铤和井壁之间的影响，正如在现场测量中经常观测到的一样(Tucker和王，1999;洪和Dhupia,2015)。

虽然有限元建模方法可以用来模拟钻柱的响应，但计算过程中需要大量的时间和时间来解决。因此，有必要发展高保真扭体参数模型，以更有效地研究钻弦动力学，特别是实时实现(Jansen, 1991;Puebla和Alvarez-Ramirez,2008;Navarro-Lopez和Cortes,2007 a)。这些模型也经常被当作真正的平台(Girsang et al.， 2013)来验证钻弦应用程序的控制性能(al - hiddabi et al.， 2003;Zamanian et al.,2007;Richard et al.,2007;Ritto et al.,2009;Yigit Chistoforou,2002)。本文采用图3所示的集总参数模型来表示钻具组合。与文献中现有的纯扭转模型相比，该模型考虑了x-y平面上钻铤的横向运动，这对于描述钻铤与井壁之间的影响至关重要。顶部的旋转机构，钻杆，钻铤和钻头分别是通过线性扭转弹簧和阻尼器连接在一起的转动惯量，如图3(a)所示。图3 (b)所示为在井眼中心上的极坐标表示横向运动，并定义了集总参数模型的DOFs。

其中T是输入转矩的电机驱动旋转机制,ki和ci分别为每个组件的有效的扭转刚度和阻尼所代表的下标iϵ{ r p、c、b、m }在图3(一)下标对应于泥。

R是钻铤的半径。

e0的偏心质量中心对领子部分的几何中心,v r r =theta;ϕ̇ ċ之间的相对线速度井壁和钻铤,m, k和c的有效质量与流体泥浆钻环,弯曲刚度和阻尼的项圈。

钻环之间的接触力Fr和井壁建模公式类似于一个线性弹簧与预定义的间隙c 0 =minus;h R(詹森,1993)

其中Rh为井壁半径，kw和cw分别为钻孔壁的刚度和阻尼系数，而w为钻铤与井壁之间的摩擦系数。

研究钻机在粘滑振动时的测量摩擦曲线，将井下摩擦转矩与井下转速联系在一起，如图4(A)所示。

这一实验测量的井下摩擦扭矩表现出一种滞后的行为和负的Stribeck曲线。

(a)钻柱集中参数模型;

(b)钻铤和稳定器横向运动的截面图。

《石油科学与工程学报》(2016)119-127 121转速。

因此，井下摩擦扭矩Tf可以用一个滞后的干摩擦模型近似(Yigit和Chistoforou, 2002;

Wojewoda et al .,2008)

图4(b)所示为(10)所示的滞回模型。

Eq.(11)描述了预滑移和加速阶段，分别为1 7和2 6来建模Stribeck曲线。

方程式。

(12)-(14)为减速阶段，其中常数为f2 0.25, f 0.32, f 0.02, v 0.6, 0.002。

值得注意的是，图4只给出了正转速，因为在钻井应用中为负转速(即:

，在反方向上的速度不能被应用，因为它将解开钻杆。

在(7)中，位岩相互作用力矩Tb可以表示为

3卡尔曼估计和LQR设计

正如前几节所讨论的，工业系统需要进行井下测量，以确定粘滑振动的发生。这些测量也需要国家空间的控制器设计在先前报告的研究工作(al - hiddabi等，2003;Zamanian et al .,2007;理查德et al .,2007;Ritto et al .,2009;Yigit Chistoforou,2002)。

然而，在实践中，测量通常只能从表面的组件中获得。因此，本文采用一种LQG控制技术，在给定恒定参考速度vref的情况下，在不进行任何井下测量的情况下，观察粘滑振动的发生，避免振动，同时调节钻柱的速度。这一技术，其原理图如图5所示，使用卡尔曼估计器来估计井下钻头的状态。然后制定了最优的LQR控制律，以减少基于估计状态的不理想振动。横向运动不包括在这一简化的单扭转模型。值得注意的是，结果控制器随后应用于在Eqs中开发的高保真模型。这被认为是评价其性能的真正的植物模型。减少阶模型的状态空间表示可以写成

仿真是在MATLAB/Simulink环境下实现的。附录a中提供它们的运动方程,(2)-(16),数值解,被分配的初始侧向位移钻铤是0.03米(1.18)和钻环之间的间隙c0井壁被设置为0.1(3.94)。作为参考案例，采用了常用的工业PI控制策略来调节表面上的顶部旋转机构的速度。经典PI控制器，基于图5中的误差。提出反馈闭环控制策略的原理图。图6所示。纯扭转减阶钻柱模型。l .香港et al。/石油科学与工程学报140(2016)119 - 2016 119转速的旋转机制,调整使用Ziegler-Nichols方法(Navarro-Lopez和苏亚雷斯,2004),这样上面旋转机制遵循一个固定的参考速度11.6 rad / s(110 RPM),这是一个典型的名义操作速度石油钻井系统(Leine et al .,2002;Navarro-Lopez和议会,2007 b)。图7显示了顶部旋转机构和井下钻具的模拟转速。尽管顶部旋转机构被控制在恒定参考值下运行，但钻头上有明显的扭转振动。钻头响应与质量一致。

通过场测量(例如图1中的一个)在周期和振幅上观察到的粘滑振动。这种扭转振动经常发生在实践中，因为PI控制器的调优没有考虑到钻头速度的原因，这通常是无法测量的。因此，尽管顶部旋转机构的速度得到了成功的调节，但下孔钻头的速度从0到29 rad/s(几乎是表面速度的3倍)，具有典型的15 s周期。除非监测到钻头的转速，否则这种现象不会引起注意。如图8(a)所示，当钻头瞬间被抓时(即:当它的转速接近于零时，驱动力矩作用于钻头上，增加到较大的值，以克服静干摩擦。然而，当钻头被释放时，摩擦扭矩随着Stribeck曲线的减小而减小，在此过程中，在钻柱中存储的能量释放会导致钻头的大量加速。在持续的粘滑振动下，钻头速度可以降至接近零。然后，由于干摩擦的滞回特性，摩擦力矩会突然增大到一个大值，如图8(b)所示。当驱动力矩大于摩擦力矩时，钻头转速会增加，循环往复。这种扭转振动的大振幅会导致较大的离心加速度，从而进一步刺激过度耦合的横向振动，如图9所示。

对于卡尔曼估计器设计，称重因子Q和R分别表示对测量和模型的信心。与模型信息相比，Q的大值与对测量信号的信心增强有关。另一方面，R的大值与对测量信号的不信任感有关。由于测量结果包括非线性扰动对模型状态的影响，而模型状态没有被假设的线性模型所捕获，因此在矩阵R中使用大值将会过滤掉这些信息，并不能根据测量(Girsang和Dhupia, 2013年)更新扰动项。乔治et al .,2008)。在这项研究中,权重因子Qfrac14;35和重量基于模拟结果的调优，计算卡尔曼增益l，验证卡尔曼估计器在识别粘滑振动发生时的有效性(如图7所示)，Eqs中描述的真实植物模型。(2)-(16)随调谐PI控制器与卡尔曼估计器增强，如图10所示。估计量的输入控制输入扭矩T和测量从真正的植物ϕϕr和ṙ,这可从顶部测量旋转机制。图11比较了钻头的估计和测量转速。可以看出，提出的线性卡尔曼估计器能够反映井下粘滑振动的发生。它还能很好地估计比特速度的振幅，这对于评估振动的严重程度至关重要。然而，当钻头在棒子区域时，估计误差会明显增大。如图12所示，这一现象是由于线性估计器无法估计非线性的预滑移相，也无法估计由于滞后效应引起的旋转速度的突然变化。

c和权重因子Rcfrac14;0.01。在这里，权重矩阵Qc被选为一个对角矩阵，每个对角线项反映了相应状态的相对重要性。因此，所选的Qc更侧重于控制速度而不是位置。一个较大的Rc值会导致更严格的控制。虽然，它会导致系统更快的响应，但也会导致执行器的饱和。

图13显示的控制响应钻柱使用提出了LQG控制策略(图5)。该控制器能够抑制任何过度振动从一开始就在30年代的模拟,通过防止钻头回落到地区,钻头后保持静止第一20多岁。这种性能在一般的工业实践中是可以接受的(National Oilwell Varco, 2012;Navarro-Lopez和苏亚雷斯,2009)。当顶部旋转机构开始驱动时，钻头仍几乎是静止的，因为摩擦特性是在非线性预滑区域。这种非线性摩擦导致了估计钻头速度的显著误差，如图14所示。然而，在钻头开始滑动后，状态估计出真正的值，从而得到令人满意的控制性能。如图13和14所示，提出的LQG控制策略能够估计滑动区域内的摩擦特性和状态，尽管保持了线性控制结构，但仍可获得可靠的控制性能。在图15中所示的估计和真实摩擦力矩之间的稳态误差可能是由于模型的订单减少和井下干摩擦的非线性引起的。尽管如此，估计的摩擦扭矩仍然提供了有价值的见解，关于井下摩擦的轮廓，没有任何井下测量。这种情况下的横向振动如图16所示，表明横向运动在瞬态后，减小为稳态旋转运动。因此，尽管估计模型没有考虑任何横向运动，但所提出的控制策略能够显著降低横向振动并防止粘滑反应。因此，提出的LQG控制策略成功地识别了粘滑振动，调节了钻柱的速度，同时抑制了扭转和横向振动。

5结论

BHA的过度扭转和侧向振动通常是钻柱过早失效和钻井效率低下的根本原因。为了减

全文共10280字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[11473]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章