
英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
永磁同步电动机自适应死区补偿方案
摘要
本文提出了一种由为获得基波相位电压的逆变器供电的适用于永磁同步电机的自适应死区补偿矢量控制系统。为补偿因逆变器的不稳定性如空载时间、设备开关时引起的及二极管导通电压所引起的干扰电压,相位死区时间补偿电压(DTCV)在转子坐标中会转换为q轴DTCV。文章研究了q轴DTCV和死区时间补偿时间(DTCT)的关系。干扰电压的检察人员推测可以使用q轴干扰电压对DTCT进行识别。同时相位DTCV的幅度可以根据检测到的DTCT自适应地进行确定。DTCT精度则是由实验计算确认的理想有效功率和实际功率的绝对平均百分误差(MAPE)。自适应的DTCT比固定DTCT的要小,同时其MAPE在任何时间都可以控制在5%以内。
关键词:死区时间补偿时间(DTCT),死区时间补偿电压(DTCV),干扰电压,永磁同步电机(PMSM),电压源型逆变器。
1 前言
在过去的十年中,由电压源型逆变器供电的永磁同步电机(PMSM)驱动器已经有过广泛的开发。也衍生出了很多应用,如需要一个基本的相电压信息的转子位无传感器驱动电机[1],[2]。由于逆变器输出端不能对基本相电压进行检测,因此通常使用指令电压来对实际电压进行代替。然而,由于逆变器的不稳定性如空载时间、设备开关时引起的及二极管导通电压所引起的干扰电压,指令电压常不会与基本相电压实际情况相一致,死区就对逆变器避免支路短路这一问题上起到了重要的作用。设备开关和导通时的电压在设备的实际使用中是不可避免的。为解决这一问题,一些研究人员尝试着对逆变器的不稳定性进行补偿[3],[4]。在[3]中,补偿是以引入死区时间补偿电压(DTCV)来实现的。DTCV是通过分析根据理想的和实际的逆变器输出功率之间的平均误差来确定的。虽然此种方实现比较容易,但设备开/关时并不能对导通电压的影响进行补偿。而在[4]中,则通过引入死区时间补偿时间(DTCT)来对这一问题进行解决。DTCT一视同仁地包括了开启/关闭时间和导通电压以及死区时间。故该方法不仅可以对死区时间效应进行补偿,还可以补偿设备开关时间和导通电压的影响。由于DTCT通常是未知参数,故有必要对DTCT进行识别。在[4]中,DTCT常由预先开发好的自适应识别程序来识别,然后再将识别出来确定的的DTCT应用于死区补偿策略。但因DTCT随着操作的不同会产生一定的变化,所以固定的DTCT也不能做到百试不爽[5]。
针对该问题,已经提出了一种使用干扰电压监测器的永磁同步电机自适应死区时间补偿方案[6]。该方法利用基于永磁同步电机理想模型研制的干扰监测器,可同步估算转子参考系中的d-q轴DTCV。而后,将估测的d-q轴DTCV值直接补偿到由电流控制器产生的d-q轴指令电压上。由于d-q轴DTCV的基频是驱动频率的6倍,所以随着驱动频率的增加会出现一定的延迟,可能会导致死区时间补偿的衰减。
本文提出了一种由为获得基波相位电压的逆变器供电的适用于永磁同步电机的自适应死区补偿矢量控制系统。当d轴电流值为零时,对DTCT和q轴DTCV之间的关系进行研究。在本文中,由于逆变器的不稳定性,假定q轴DTCV值等同该轴干扰电压值。q轴干扰电压由干扰监测器得到。DTCT由估计的q轴干扰电压进行计算。利用自适应DTCT来确定DTCV位幅。该方案的优点是,仅对相位DTCV的幅值进行调整,所以对干扰监测器的估值延迟影响都较小。此外,自适应死区时间补偿策略仅对q轴干扰电压监测器有要求。理想和实验结果均证实了文中方法的可行性和有效性。
图1. 坐标定义
图2.变速矢量控制的永磁同步电机驱动系统配置。
2 永磁同步电机驱动系统
A.坐标轴的定义
图1所示为本文中对于坐标轴的定义。a-b-c轴定义为每相电流的磁通量方向。d轴则定义为永磁体磁通量定向。q轴定义轴向前90°步进的方向。d-q轴与永磁同步电机的转子同步。
B.系统配置
图2所示为典型的矢量控制永磁同步电机驱动系统的配置图。文中所提到的死区时间补偿器由虚线框圈定。该补偿器的细节会在第四部分进行阐述。由于永磁同步电机的原理是从转子获得励磁,而在典型的矢量控制型永磁同步电机驱动器中,励磁分量的d轴电流通常设置为0.在第三届中,也会对d轴电流为0情况下的DTCT进行阐述。
3 死区补偿
A. 用公式来表示DTCV
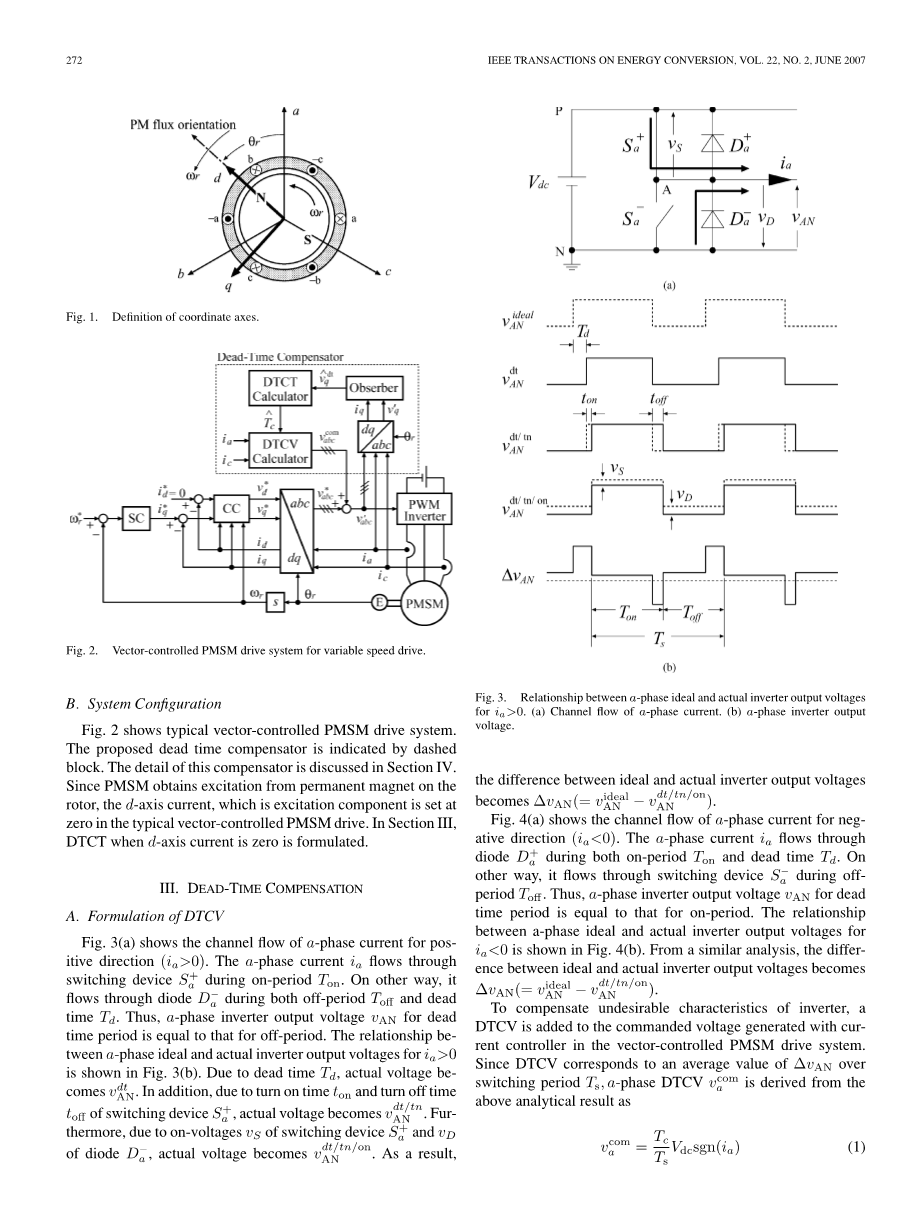
图3(a)表示正向(iagt; 0)的a相电流流向。在接通时间Ton内,alpha;相电流ia会流过开关器件S a。另一方面,在关闭时间Toff和死区时间Td内,电流流经二极管Da-。因此,死区时段的a相逆变器输出电压vAN值与关闭时间内相应值相等。 a相理想和实际输出电压之间的关系iagt;0如图3(b)所示。由于死区时间Td内,实际电压变为vdtAN。此外,由于连通时间ton和开关器件S a的关断时间toff,实际电压会变为。更此外,由于开关器件S a和二极管Da-的导通电压vS和vD,实际电压应为由此,理想和实际的逆变器输出电压之间的差异变为
图3. a相理想和实际输出电压之间的关系为iagt; 0。(a)a相电流流动线路。(b)a相逆变器输出电压。
图4(a)表示的是逆向的a相电流(ia lt;0)流向。在接通周期Ton和死区时间Td内,a相电流ia流过二极管Da 。另一方面,在关断时间Toff期间流经开关S-a。因此,死区时段的a相逆变器输出电压vAN等于接通时间段的a相逆变器输出电压vAN。图4(b)显示了ia lt;0的a相理想和实际逆变器输出电压之间的关系。进行类似的推理可得,理想和实际逆变器输出电压之间的差异为:
图4. a相理想和实际输出电压之间的关系为ialt; 0。(a)a相电流流动线路。(b)a相逆变器输出电压。
为了补偿变频器的不稳定性,在矢量控制型永磁同步电机驱动系统中,电流控制器产生的指令电压中会加上DTCV。由于DTCV在开关周期Ts内对应于Delta;vAN的平均值,故从上述结果导出a相DTCV 的为
式中TC、Ts、Vdc分别为DTCT,开关周期,和直流母线电压。DTCT定义为:
式中Td,ton,toff和Von分别是死区时间,导通时间,断路时间和平均导通电压。平均导通电压Von定义为:
其中vD,vS分别为二极管和开关元件的导通电压,Ton,Toff分别为逆变器支路上叉的闭合周期和断路周期。此处须注意,因为对igt; 0,接通周期Ton几乎与断路周期Toff相同,正负向电流流向的平均导通电压几乎相同,反之亦然。同理,还可导出b相和c相DTCV。
表1 受测逆变器规格
图5. 受测变频器的二极管和IGBT晶体管的导通电压。
B.开关和二极管的导通电压
表I表明了受测变频器的规格。开关元件采用的是绝缘栅双极型晶体管(IGBT)模块。 IGBT的死区时间设置为5mu;s。
图5中显示了二极管和IGBT的导通电压相电流的均方根(RMS)值。数据结果由数字示波器TDS3014B测量。测试过程汇总,测得的逆变器,二极管导通电压大于IGBT(vDgt; vS)。那么就可以认定,无论相电流的RMS值如何,所测得的导通电压都是定性的与规格一致。从(3)中可以看出,当相电流RMS值固定—即负载条件恒定时,igt;0的情况下平均导通电压Von随转子速度的减小而增加,低速区的Ton小于高速区的Ton,那么可得Von受控于vD而非vS。同理也适用于ilt;0的情况。另一方面,当二极管和IGBT的导通电压随相电流的RMS值而变化,这种情况下即使保持了转子的速度,平均电压Von也会随负载而变化。此外,由于寄生电容[5]的存在,断路时间会随操作点而变化。因此,表I中列出的导通电压和断路时间也不是普适的。即:DTCT随操作点变化。因此在各操作点对这一参数单独测量都是比较困难的问题,所以本文中所采取的DTCT均为在线测量得来。
4 DTCT的在线确定
A d-q轴上的DTCV
图6显示了逆变器供电的永磁同步电机驱动器的多种DTCV数值结果。在这些数值结果中,PMSM的转子速度为1500r/ min(频率为50Hz)。d轴电流id设置为零。期望DTCT为Tc,开关周期Ts和dc连接电压Vdc分别被设置为3,200mu;s和200V。
图6 d轴电流为零时DTCV值[ 50Hz(1500 r/min),2A]。(a)a相电流。(b)a相 dtcv。(c)转子位置的电角度。(d)d-q轴的DTCV。
图6(a)表示a相电流ia。 由于DTCV的极性受相电流极性的控制,所以如图6(b)所示,通过(1)来对a相DTCV确定。虽然此图中未显示b和c相的DTCV波形,但可以通过上述方法进行确定。图6(c)表示PMSM的转子位的电角度theta;r。此处,当d轴电流为0时,转子位置的零点对应a相电流ia的零时刻。使用下列变换矩阵将公式(1)所示的阶段DTCV转换成d-q轴DTCV:
如图6(d)所示,q轴DTCV是带脉冲的直流电压。q轴DTCV的最大值由下式得:
须注意,只要开关周期Ts和dc链路电压Vdc为常数,其最大值就与DTCT Tc成正比。也就是说,随Tc变化。另一方面,d轴DTCV是交流电压。其幅度可表示为。d-q轴DTCV在转子位置每经过pi;/ 3弧度时发生变化,即可知d-q轴的基频为DTCV的6倍。
表II总结了当id = 0时转子位置的d-q轴DTCV理论值。从表Ⅱ得出平均q轴DTCV值都在pi;/3弧度以上表示为:
表2 当id=0时d-q轴DTCV理论值
B.DTCT的确定
相DTCV对应于设备开关周期内理想和实际逆变器输出电压之差的平均值。确定DTCV的值对死区补偿至关重要。从(1)可以看出,只要开关周期Ts和dc链路电压Vdc都是常数,相位DTCV的振幅就与DTCT Tc成正比。DTCT通常是未知参数。此外,如第三部分所述,DTCT随操作点而变化。然后经由专门手段获取DTCT。
对(5)重新进行整理得出DTCT分析方程:
由于直流链路电压Vdc和开关周期Ts是已知参数,故为计算DTCT,我们仅估计最大q轴DTCV。DTCT则通过以下步骤来进行确定。假设矢量控制型永磁同步电机驱动系统中电流控制回路中逆变器不稳定性产生d-q轴干扰电压()。由于要补偿的q轴干扰电压vdt对应于q轴DTCV ,所以其最大值为。q轴干扰电压vdt由干扰监测器进行估计。估计的q轴干扰电压的最大值为。然而,当估算的q轴电压不稳定,求测q轴干扰电压的可靠峰值就比较困难。为解决这一问题,就采取了基于平均q轴DTCV 而非最大q轴DTCV 的方法来识别DTCT。从(6)和(7)导出DTCT Tc和平均q轴DTCV之间的关系:
关于估算的q轴平均扰动电压对DTCT进行识别的方程:
因与d轴有关,由表2可得,可以用d轴干扰电压进行估计。然而,又因d轴干扰电压的基频超过干扰监测器的带宽,所以当达到一定速度时d轴干扰电压估计最大值与d轴DTCV的最大值不等。另外,由于d轴DTCV的平均值在理论上等于零,所以d轴电压的估计平均值对于识别到的DTCT几乎无效。相反,(9)中由于q轴扰动电压是直流电压且其平均值可被用于计算DTCT,所以计算中不会增加误差。出于以上考虑,最终我们选择使用q轴干扰电压计算DTCT。
C q轴估计干扰电压
本文主要研究矢量控制型永磁同步电动机的死区补偿问题。针对q轴干扰电压的观测器是由转子参考系中永磁同步电机的电压方程导出的。其方程为:
其中R,L和p分别是电枢电阻,电枢电感和微分算子。去耦电压表示为:
式中omega;r和Ke分别是电角速度和电动势(emf)常数。
电流控制器产生的指令电压随干扰电压()的增加而增加,死区时间补偿策略用以减小干扰电压下的电流误差。电流控制回路的电压方程表示为:
上标“*”表示指令电压值。因此,指令电压与实际电压数值不相一致,即(12)与(10)不一致。
相反的,电流控制回路的死区时间补偿策略的电压方程表示为:
从式(13)中可见,只要d-q轴的DTCV()与d-q
全文共8856字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[11370],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


