
英语原文共 5 页,剩余内容已隐藏,支付完成后下载完整资料
基于缸体振动分析的柴油机曲轴扭转扭振分析
摘要:
通过实验研究了汽车柴油机扭振曲轴振荡问题,并考虑了其与汽缸体振动的关系。 已经证实,不仅在共振谐波而且在较高频率下出现的振动是由于曲轴的振荡振荡引起的,这在曲轴的滑动轴承中产生了冲击。
关键词:
振动,阻尼器,扭转振荡,滑动轴承
正文:
为了确保所需的曲轴强度,需要进一步研究由不均匀转矩产生的柴油发动机中的曲轴的扭转振动。
最近,当使用增压柴油发动机时,已经注意到曲轴扭转振荡的不良后果,例如噪音,振动,过量燃料导致的油消耗以及驱动运转中断[1-3]。 在活塞油泵驱动时,如[1]中所述,当扭转振动不平衡时,每个齿轮齿上的载荷增加50-60倍。 这会导致齿轮的凹陷和断裂。 在目前的柴油发动机的车辆和卡车中,使用高压燃料泵,其点火能量较高。 这会增加产生的扭矩的不均匀性,并导致驱动器中的扭转振动相互抵消,从而可能导致断裂[3]。 为了使驱动装置在高压燃料泵中可靠运行,采用了阻尼扭转振荡的系统。
扭转振动通过扭转传感器来测量。 在测量中,很难选择传感器位置并确保从旋转曲轴上获取和分析信号。 为了安装传感器,通常需要根据曲轴尖端改变常规设计结构。 因此,考虑的实际振荡器系统可能不符合常规系统。
我们知道,在汽车柴油机中,曲轴顶端的扭转角最大,而扭转振动的节点靠近飞轮。 扭转曲轴振荡与气缸体振动之间的关系是从扭转传感器和压电加速度计的读数同时确定的。 传感器安装在曲轴的顶端,而加速度传感器则通过销钉固定在气缸体第一个冠轴承的垂直于曲轴轴线的张紧螺栓上,并且水平定向。 在V8H12 / 12柴油发动机上进行了测试。
图1 V8H12 / 12柴油机的转速特性
图1 V8H12 / 12柴油机的转速特性
在图1中,我们展示了柴油机的速度特性。 在附图中, 在图2和图3中,我们显示了曲轴顶端的扭转图,分析了至少十个柴油机运转周期。 使用计算机将模拟信号数字化,确定曲轴顶端扭转角的最大幅值,并计算平均值。 为了确定谐振谐波,我们使用了快速傅立叶变换。 请注意,实验数据图。 2-5适用于非标准配置的发动机,其中液压离合器由安装扭力传感器的专用动力选择板代替。
图2柴油机曲轴尖端的扭转角度根据图1中的速度特性曲线,不带(1)和(2)带有扭转减振器:6.5,7,8,12,13。 谐振谐波的数量。
图3. n = 1900 rpm时曲轴尖端扭转角的谱图。
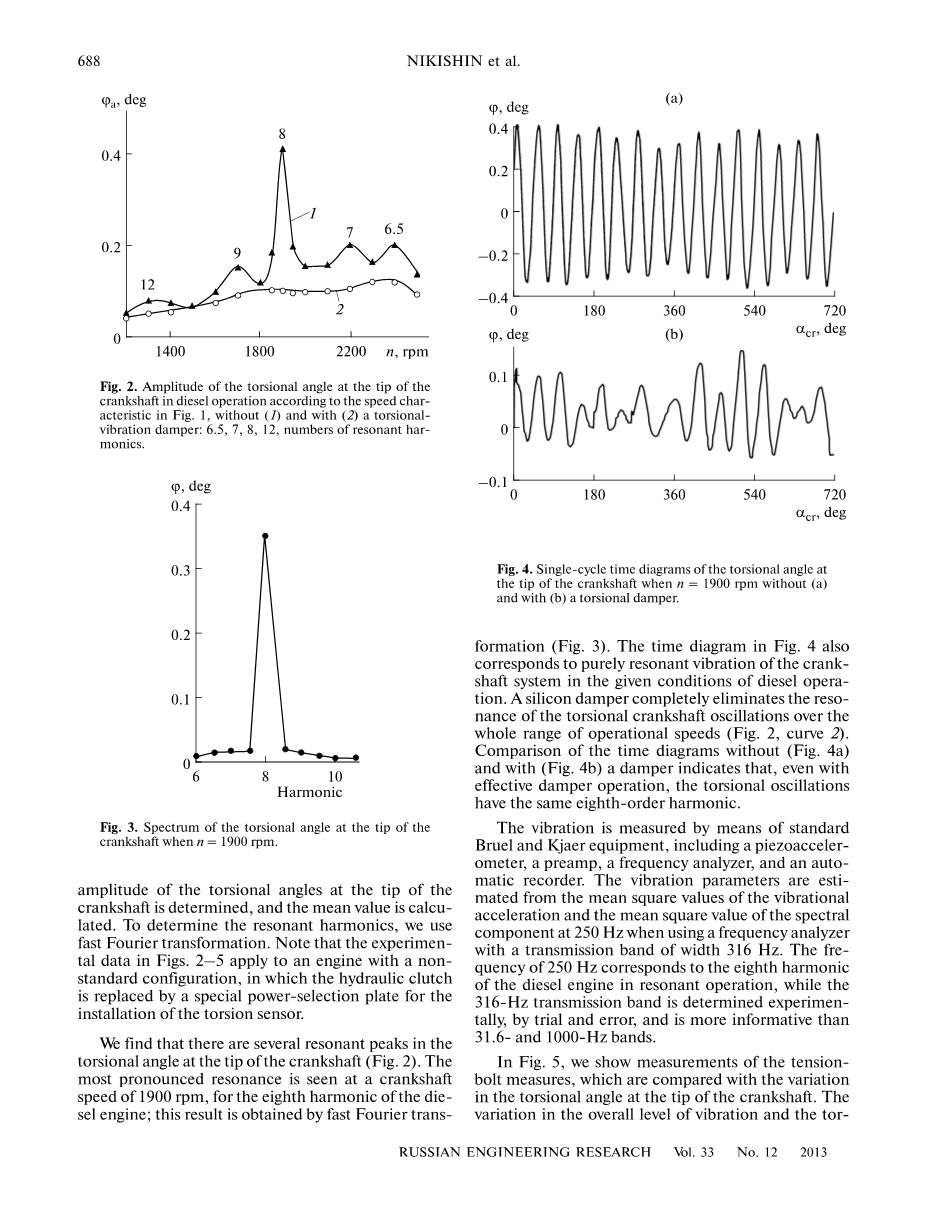
图4.(a)和(b)扭转阻尼器时,当n = 1900 rpm时曲轴顶端扭转角的单周期时间图。
我们发现曲轴顶端的扭转角有几个共振峰(图2)。 在1900rpm的曲轴速度下,对于模具自身发动机的八次谐波,看到最明显的共振; 这个结果是通过快速傅里叶变换得到的(图3)。 图4中的时间图也与柴油机给定条件下曲轴系统的纯共振相对应。 硅阻尼器完全消除了在整个运行速度范围内扭转曲轴振荡的共鸣(图2,曲线2)。无阻尼器(图4a)和阻尼器(图4b)的时间图的比较表明, ,即使有效的阻尼器操作,扭转振荡也具有相同的八次谐波。
振动通过标准布鲁尔和克亚尔设备进行测量,包括压电加速度计,前置放大器,频率分析仪和自动记录仪。 振动参数由振动加速度的均方值和频率分量在250 Hz时的均方值估算,当频率分析仪的传输频带宽度为316 Hz时。 250Hz的频率对应于共振操作中的柴油发动机的八次谐波,而316Hz的传输频带通过试验和误差实验确定,并且比31.6和1000Hz频带更具信息性。
图5缸体中拉力螺栓振动的依赖性曲轴顶端的扭转角度对曲轴转速n的影响:(a)250Hz部件的振动水平; (b)整体的振动水平; (c)扭转角度。
在图5中,我们显示了张力螺栓测量的测量结果,这些测量结果与曲轴顶端扭转角度的变化进行比较。 整体振动水平的变化和曲轴顶端的扭转角度是相同的。与整体振动水平相比,与扭转角度的相关性对于250Hz分量的水平更好。 我们可以说第一个冠轴承的张紧螺栓的振动定性地表征了扭转曲轴的振动。这种测量方法也可以用来评估扭转振动阻尼器的有效性。
图6.没有传感器适配器的气缸体中的张紧螺栓振动:(a)250 Hz部件; (b)光谱在n = 2000rpm。
由于扭转测量采用修正后的振动系统进行,因此我们需要评估常规系统的振动。为此,我们只测量张力螺栓的振动,不测量扭转传感器的适配器(图6)。分析图。图6和5显示了扭转曲轴振荡的共振从1900rpm转变到2000rpm。在图6b中,我们显示了图1中速度特性的柴油发动机在(1)和没有(2)扭转阻尼器的情况下的拉力螺栓的振动频谱。在没有阻尼器的情况下,振动的总体水平由高频分量(600-3000Hz)确定,如同在频率范围200-400Hz中所清楚看到的那样。这表明了振动和扭转振动之间的关系。低频区域(150Hz以下)由倾斜转矩的不均匀性形成。乍看之下,高频区似乎与扭转曲轴振荡无关,但安装液体阻尼器不仅在八次谐波的谐振频率处改变频谱,而且在高频区也改变频谱。
图7曲轴在扭转振动作用下的运动:(1)曲柄销; (2)冠针。
从图7可以看出,在振幅为phi;a的扭转曲轴振荡中,曲柄销移动距离Delta;a= r tanphi;a,其中r = 60 mm是曲轴半径。因此,当phi;a= 0.4°时,曲柄销运动的幅度为0.42mm,因此双幅度为0.84mm。由于轴承间隙为0.07-0.117毫米,因此我们得出的结论是曲轴销会对曲轴轴承产生影响。当曲柄销半径Rcp = 42.5mm时,双幅度为0.6mm;影响将再次发生。为了得出这个结论,我们使用阻尼器来测量振动(图5a)。从图2可以看出,阻尼器完全消除了共振振动并将扭转角降低到了0.1°。相应地,曲柄销运动的幅度减小了四倍,达到0.1mm。但是,这对轴承的冲击足够了。在振动频谱中,250和320 Hz处的分量减少了三分之一,这非常接近于扭转角的减小。高频振动减少了2-7倍,尽管它们是频谱中的主要决定因素。
图8. 191 kW柴油机曲轴前端扭转角随曲轴转速n的变化曲线,没有(1)和(2)有一个扭转阻尼器:5,5.5,6.5,7,8 ,谐振谐波的数量
图9曲轴尖端扭转角度和张力螺栓振动的振幅:(1)整体振动水平的均方值; (2)扭转角; (3)在250Hz处的振动水平的均方值。
在V8H12 / 12柴油发动机的不同超级充电情况下进行类似的测试:额定转速为2600 rpm时的额定功率为191 kW(图8-10)。 在柴油机操作中,在速度特性上记录了四个共振。最明显的是在n = 1850和2700转/分时,对应于8和5.5次谐波。由于n = 2700 rpm不是主要操作频率,因此注意力集中在n = 1850 rpm。在这种情况下,phi;a= 0.311°,比额定转速为2200rpm的162kW柴油发动机小1.3倍。在图8中,我们还显示了硅扭转阻尼器的结果。在1850和2700转时,阻尼器形式不同。扭力角在1850rpm下降至0.065°,在2700rpm下降至0.15°。效率相应地提高了4.8倍和2.1倍。整体振动水平和250 Hz分量与扭转角度相对应(图9)。在图10中,我们展示了共振时的振动频谱。与图。如图6所示,在1500-3000Hz处存在明显的高频分量。 2000年的振动水平以3-6倍的系数高于其他组件。
图10.共振时张力螺栓振动的频谱(n = 1850rpm)。
因此,扭转曲轴振荡与缸体振动相关。 可以通过测量气缸体中第一个冠轴承处的张力螺栓振动来确定曲轴振动的频率。 从高频区域的振动水平可以看出,曲轴滑动轴承产生的扭转振动
内燃机曲轴组件的非线性扭转振动特性
摘要:
曲轴总成故障是影响发动机可靠性和使用寿命的主要因素之一。已经普遍应用于发动机曲轴组件动态建模的线性集中质量法显示出明显的模拟误差。曲轴组件的非线性动态特性对于提高建模正确性具有指导意义。在本文中,基于瞬时动能等效方法推导出曲轴组件非恒定惯性的一般表达式。考虑非线性因素的拉格朗日法则建立了多缸曲轴组件的非线性动力学方程,例如往复运动部件的非恒定惯性和轴段的结构阻尼。采用特征向量法研究曲轴组件的固有频率和振型。使用数值积分方法研究考虑非恒定惯性的柴油机曲轴组件的强制振动响应。将仿真结果与集总质量模型和使用系统矩阵方法的详细模型进行比较。非线性扭转振动分析的结果表明,由非恒定惯性产生的附加激励转矩激活二阶滚动振动,并且由非恒定惯性产生的附加阻尼转矩是主要的非线性因素。高阶激励力矩引起的扭转角位移增大与非恒定惯性有关。本研究课题旨在改善非线性动力学理论,并将确定的非线性参数用于曲轴组件的结构设计。
关键词:
内燃机,曲轴总成,非恒定惯性,非线性振动,扭转振动特性
介绍:
车辆发动机功率密度的增加导致在较宽的发动机转速范围内的励磁转矩增加,并对曲轴组件产生严重的扭转振动问题。 同时,立法规则和舒适的驾驶要求要求发动机具有高噪音,振动和不平顺(NVH)性能[1-3]。 曲轴组件的动态模拟在解决这些问题的曲轴设计中起着越来越重要的作用。
曲轴是一个非常复杂的连续质量体系。动态建模方法包括系统矩阵法,有限元法(FEM)和多体动力学法(MBD)。采用系统矩阵方法的传统集总质量模型已被广泛使用。理论计算与实验评估比较表明,理论计算中存在较大误差,低速时可达到15%[3-4]。假设动态参数是不变的是这些错误的主要原因之一。往复运动部件(活塞和连杆的小端)的位移和角速度随着曲轴运动而变化,并且与曲柄角保持复杂的函数关系,这引起曲轴组件的非恒定惯性[5-7] 。材料非线性,活塞衬套的非线性摩擦以及轴承内的油膜导致非线性刚度和阻尼[8-9]。此外,扭转振动吸收器和弹性耦合表现出更强的非线性[7]。通常,非线性参数在实际建模中被线性化,这不可避免地引起模型误差。因此,建立非线性动态参数的精确表达式至关重要。
GUZZOMI等人[10]研究了活塞摩擦对曲轴固有频率的影响。 XIANG等人[6]的研究表明,非恒定惯性的引入对曲轴扭振特性,如固有频率,临界速度区域和扭转振动角位移有显着影响。朱等人[7]考虑了曲轴非恒定惯性,非线性干摩擦以及活塞和缸体之间的非线性弹性。仿真结果表明,活塞与汽缸之间的非恒定惯性和非线性干摩擦对曲轴系统的非线性振动性能有较大影响。 BRUSA等[11]建立了曲轴的一般非恒定惯性模型,研究了阻尼系数对系统响应稳定性的影响。 METALLIDIS等[12]表明,非恒定惯性的引入使得曲轴的转速波动相当大,而对平均转速几乎没有影响。
根据以上参考文献,非线性参数对曲轴组件的扭转振动特性具有很大影响。基于瞬时动能当量建立非恒定惯性与曲轴转角之间的函数关系是一种经过批准和有效的方法。然而,没有发现分析处理非恒定惯性的简化和详细表达式之间的差异。大多数参考文献在其分析中没有考虑扭转振动吸收器和负载(测力计),这与曲轴组件的实际结构不同。他们讨论了由非恒定惯性引入的附加扭矩,但尚未研究气缸燃烧气体扭矩和往复惯性扭矩对曲轴扭转振动特性的影响。
使用瞬时动能等效方法推导出曲轴组件的非恒定惯性的一般表达式。 利用拉格朗日法则建立了基于非恒定惯性的动力学模型,包括扭振减振器和测力计。 同时,使用系统矩阵方法建立了集中质量模型和更详细的动态模型。 应用数值积分法模拟非恒定惯性对曲轴扭振特性的影响。 对不同模型的仿真结果进行分析和比较,以确定非线性因素。
1.曲轴组件的动态建模
1.1扭转振动力学建模
我们使用了一台道依茨 TCD2015 V06 4V柴油发动机作为研究对象。 主要技术参数如表1所示,其三维图如图1所示。基于集中质量法建立曲轴动力学模型。 该模型由气缸,扭转减振器,弹性联轴器和测力计组成,同时考虑到气缸阻尼和轴内部阻尼。 该模型被称为非恒定惯性模型。 图2示出了具有十一自由度(DOF)的曲轴组件的力学模型,其中后缀0是测力计,1是飞轮,2-7是曲柄,8是过渡轴,9是带轮 和粘性阻尼器毂,10是扭转振动吸收器的惯性质量。
GT-CRANK V6.2搭建了一个更详细的动力学模型,其中一个曲柄被离散成一个轴颈,一个腹板和两个半曲柄销。 同时考虑了轴承油膜动态润滑和活塞 - 缸套摩擦。 集中质量模型也有11个自由度,曲柄连杆机构的惯性按传统方法获得。
1.2单缸瞬时惯量表达式的推导
曲柄沿其轴线旋转,而活塞通过连杆来回往复运动。 因此,曲柄连杆总成可简化为曲
柄滑块机构,其结构参数和示意图如图3所示。如图3所示,A,B,G,Gcent;分别代表大端 轴承位置,曲轴销位置,曲轴质量中心和连杆质量中心。 h,j表示OA与OG和AGcent;与AB的长度比。 r,D,l分别是曲柄半径,气缸内径和连杆长度。 theta;,gamma;,delta;是曲柄角度,连杆角度和活塞偏移量。
|
参数 |
描述和价值 |
|
发动机型式 钻孔D / mm 行程S / mm 连杆长度r / mm 压缩比εc 最大功率Pe / k W 最大功率转速np /(rbull;min) 最大转矩转速nt /(rbull;min-1) 发火顺序 |
V6涡轮增压中冷器柴油发动机
132<!-- 全文共10775字,剩余内容已隐藏,支付完成后下载完整资料 资料编号:[9413],资料为PDF文档或Word文档,PDF文档可免费转换为Word |


