
英语原文共 10 页,剩余内容已隐藏,支付完成后下载完整资料
关于向外传播球形火焰的层流火焰速度与Markstein长度数据提取的研究
Zheng Chen
State Key Laboratory for Turbulence and Complex Systems, Department of Mechanics and Aerospace Engineering, College of Engineering, Peking University, Beijing 100871, China
翻译:李凡奇
摘 要:不同的研究人员采用相同的定压球形火焰法对甲烷/空气混合气体进行研究时,观测到的层流火焰速度及Markstein长度存在巨大差异。为了减小这种差异,用于从球形传播火焰中获取层流火焰速度和Markstein长度的一种线性模型(LM,被拉伸火焰速度与拉伸率成线性关系)和两种非线性模型(NM I 和NM II,被拉伸火焰速度与拉伸率成非线性关系)得到广泛研究。研究发现LM、NM I和NM II的精度和性能很大程度上依赖于Lewis数。经证明,NM I在混合气体的Lewis数较大(Markstein长度为正)时最准确,同时,NM II在混合气体的Lewis数较小(Markstein长度为负)时最准确。因此,为了从球形火焰实验中获取到准确的层流火焰速度和Markstein长度,不同的混合气体应采用不同的非线性模型。数值模拟和实验研究进一步证明了理论结果的有效性。此研究的结果可以直接运用到测量层流火焰速度和Markstein长度的球形火焰实验中。
关键词:数据提取 层流火焰速度 Markstein长度 球形传播火焰
- 引言
层流火焰速度被定义为平面、一维火焰锋面,相对未燃气体,沿其表面法向传播的速度[1]。它是可燃混合气体最重要的参数之一。准确测定层流火焰速度对发展和验证化学动力学机理来说是极其重要的[2]。Markstein长度是可燃混合气体的另外一个重要参数,它表征了外部拉伸引起的局部火焰速度变化,决定了有关优先扩散的火焰不稳定性[3,4]。Markstein长度同时也是某些预混湍流燃烧模型的基本输入参数之一[5]。因此,准确测定Markstein长度对湍流燃烧建模来说是非常重要的。
在过去的50年间,测定层流火焰速度和Markstein长度相关实验的新技术研发和现有方法改进得到了人们的广泛关注。采用不同火焰结构的各种实验方法(在参考文献[1,6]中回顾)都取得了发展。目前,得益于其简单的火焰结构和明确定义的火焰拉伸率,定压球形燃烧法[7-19]成为测量层流火焰速度和Markstein长度的最好方法之一。在这种方法中,封闭容器中的静止均值可燃混合气体被电火花从中心点燃,产生向外传播的球形火焰。火焰锋面轨迹,,被采用纹影法或影像法的高速摄像机所记录。接着通过不同的理论模型(后述)来提取层流火焰速度和Markstein长度。
最近一段时间,人们在采用定压球形火焰法提取层流火焰速度和Markstein长度的研究当中投入了大量工作。例如,有关着火[20,21]、辐射[22]、非球面几何[23]、压缩[24]、火焰不稳定性[25]和非线性外插法[26]等方面的影响效应已经得到了研究。然而,采用相同燃料的不同研究人员对层流火焰速度和Markstein长度的测量值依然存在差异,在文献中[27,28]能找到相关报告,这
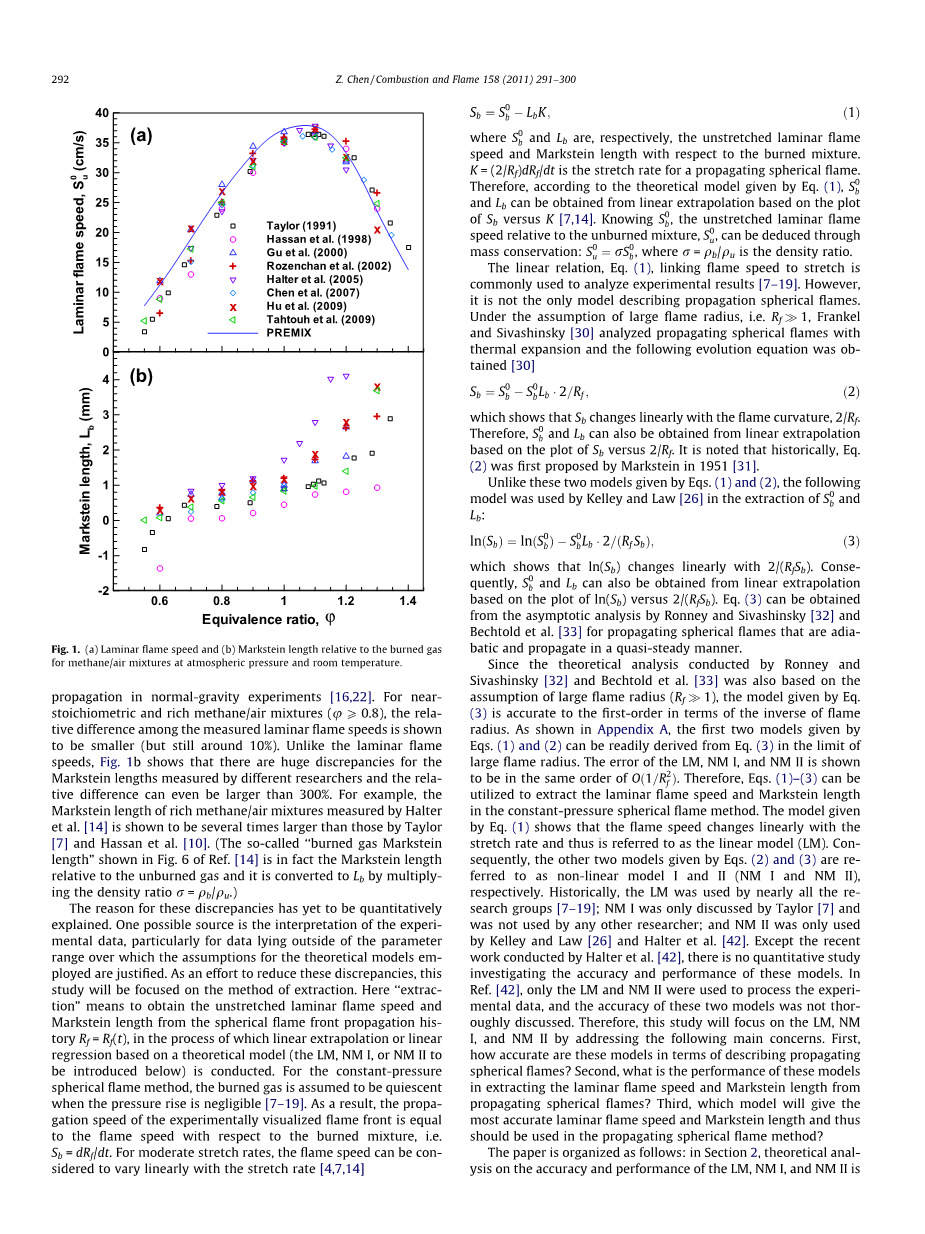
一情况成为了动力学机理验证的关注焦点。例如,图1表示对甲烷/空气混合气体测得的层流火焰速度和与相对于已燃气体的Markstein长度。除了由PREMIX计算所得的层流火焰速度外(实线表示)[29],所有的实验结果(符号表示)都使用定压球形火焰法测量[7,10,12-14,17-19]。图1a显示,对于非常稀薄的甲烷/空气混合气体(),不同研究人员测量的层流火焰速度存在很大的差异。这是由于在标准重力的实验中,浮力在很大程度上影响了球形火焰的传播[16,22]。对于近化学计量比和浓甲烷/空气混合气体(),层流火焰速度测量的相对偏差显得小一些(但仍接近10%)。不同于层流火焰速度,图1b显示,不同的研究人员测量的Markstein长度存在非常大的差异,相对偏差甚至超过了300%。例如,对于浓甲烷/空气混合气体,Halter et al.[14]的测量值比Taylor[7]和Hassan et al.[10]的测量值大数倍。(参考文献[14]的图6中所谓“已燃气体Markstein长度”实际上是相对于未燃气体的Markstein长度,乘密度比可以转换为)
这些偏差尚不能定量解释。一种可能是,偏差来源于实验数据的判读,当数据超出所选用模型理论设定的合理参数范围时尤为明显。为致力于减小这种偏差,
图1 标准大气压室温下甲烷/空气混合气体相对于已燃气体的(a)层流火焰速度和(b)Markstein长度。
本课题的重点将会放在数据提取的相关方法上。这里的“提取”是指从球形火焰锋面轨迹获取未拉伸层流火焰速度及Markstein长度,采用基于理论模型(后面将介绍的LM、NM I或NM II)的线性外插或线性回归分析方法。在定压球形火焰法中,当压升可以忽略时,可以假定已燃气体是静止的[7-19]。其结果是,在可视化实验中,火焰锋面传播速度等于相对已燃混合气体的火焰速度,即。在拉伸率处于中等大小时,可认为火焰速度随拉伸率线性变化[4,7,14]
(1)
这里的和分别是未拉伸层流火焰速度和相对已燃气体的Markstein长度。是球形火焰传播的拉伸率。因此,根据等式(1)所给出的理论模型,可采用线性外插法从对的图形中[7,14]获取和。知道后,关于未燃混合气体的未拉伸层流火焰速度可以通过质量守恒推导出来:,此处的是密度比。
等式(1)是联系火焰速度和拉伸的线性关系式,经常用来分析实验结果[7-19]。然而这并不是描述球形传播火焰的唯一模型。在火焰较大半径假设下,即,Frankel和Sivashinsky[30]分析了球形传播火焰的热膨胀并得出了下列的发展方程[30]
(2)
此方程表示随火焰锋面曲率线性变化。因此,和也可以从对的图形中通过线性外插法获取。值得指出的是,等式(2)由Markstein在1951年第一次提出[31]。
不同于等式(1)和等式(2)给出的两个模型,下列模型是Kelley和Law[26]在提取和时所使用的:
(3)
此方程表示随线性变化。因此,和也可以从对的图形中通过线性外插法获得。对于绝热、准稳态传播模式下的球形传播火焰,Ronney、Sivashinsky[32]和Bechtold et al.[33]通过渐进分析可得出等式(3)。
由于Ronney、Sivashinsky[32]和Bechtold et al.[33]进行的理论分析同样基于火焰大半径()的假设,等式(3)给出的模型在一阶下,相对火焰半径的倒数是准确的。如附录A所示,在火焰大半径的条件下,由等式(1)和等式(2)给出的前两个模型易由等式(3)推导出来。LM、NM I和NM II的误差被证明与同阶。因此,在定压球形火焰法中,等式(1)-(3)可以用来提取层流火焰速度和Markstein长度。等式(1)给出的模型显示火焰速度随拉伸率线性变化,因此被称作线性模型(LM)。同样地,等式(2)和等式(3)给出的另外两个模型分别被称为非线性模型I和非线性模型II(NM I和NM II)。从历史上看,几乎所有研究团队[7-19]都使用LM;NM I仅被Taylor[7]讨论过,没有被其他研究者使用过;NM II仅被Kelley、Law[26]和Halter et al.[42]使用过。除了最近由Halter et al.[42]主导的工作,目前没有关于这些模型精度和性能的定量研究开展。在参考文献[42]中,仅使用了LM和NM II来处理实验数据,并且也没有彻底讨论这两种模型的精度。因此,本课题主要通过讨论下列几个问题来研究LM、NM I和NM II。第一,这些模型在描述球形传播火焰时精度如何?第二,使用这些模型从球形传播火焰提取层流火焰速度和Markstein长度的性能如何?第三,哪个模型能给出最准确的层流火焰速度和Markstein长度,并应在球形传播火焰法中使用?
本论文的行文结构如下:在第二小节中,主要从理论上分析LM、NM I和NM II的精度和性能;接下来在第三小节中,运行数值模拟以验证理论分析所得出的结论;第四小节对LM、NM I和NM II处理文献中获取到的实验数据的具体性能进行评估;在第五小节给出最后总结。
- 理论分析
向外传播球形火焰已经通过渐进技术得到过分析[30,32-35]。然而,这一系列的研究都是基于规范化的火焰半径(,此处的是平面绝热火焰的厚度)假设的。因此,参考文献[30,32-35]中的理论结果不能用于评估LM、NM I、和NM II的精度,并且,所有这些模型在一阶下相对是准确的(在附录A中证明)。近期只有He[36]和Chen、Ju[37]的研究工作涵盖了所有的球形火焰尺寸,并实现了小半径火焰(着火后的火核以及火球)与大半径火焰(球形传播火焰以及平面火焰)之间的过渡。因此,本文将利用参考文献[37]的理论结果来检验LM、NM I、和NM II的精度和性能。
采用理论分析的方法来研究LM、NM I、和NM II有两条主要优点:(1)理论分析中可得到层流火焰速度和Markstein长度的精确值;这两个精确值可与提取值进行比较,从而能严格评估不同外推法的精度。(2)理论分析中可以得到被拉伸层流火焰速度和拉伸率的精确值;从而来自于浮力、着火、非球面几何、辐射、压缩的影响以及计算导数的误差都可以得到消除。
本课题所采用的理论分析方法[37]的局限在于:未考虑热膨胀的影响,并且假定球形火焰锋面的传播是准稳态的。就作者所知,学术上所有的球形火焰理论都认为热膨胀是基于火焰大半径假设的,因前文所述原因而不能用于评估LM、NM I、和NM II。不过,在第三节中详细讨论的数值模拟将会考虑到热膨胀以及非稳态转化,从而验证LM、NM I、和NM II精度、性能理论评估的有效性。
2.1. 不同模型及其精度
对绝热条件下的自由态球形传播火焰,我们有如下火焰传播速度(由平面绝热火焰速度规范化得到)与火焰半径(由平面绝热火焰厚度规范化得到)的代数关系[37]
(4)
此处的、和分别代表Lewis数、Zelrsquo;dovich数以及已燃气体相对未燃气体的密度比[37]。Zelrsquo;dovich数被定义为,式中和分别表示活化温度和平面绝热火焰温度[37]。用数学方法解等式(4),我们能得到作为火焰半径的函数[21,37]的火焰速度精确解。由于等式(4)同时适用于大半径和小半径的球形传播火焰,它被称作为精细模型(DM)[21]。在火焰大半径()条件下,DM退化为简化模型(SM)[21]:
(5)
对于弱拉伸火焰,被拉伸火焰速度接近于绝热未拉伸火焰速度(即,此处)。在此条件下,等式(5)退化为在一阶下对准确的模型(如图三所示):
,,
, (6a-c)
此处的表示规范化Markstein长度(由平面火焰厚度规范化得到),与绝热预混逆流火焰推导出的结果相同[38]。等式(6a-c)是等式(1)-(3)的无量纲形式。因此,等式(6a-c)给出的模型也分别被称为LM、NM I、和NM II。
LM、NM I、和NM II的精度可以通过与DM比较来评估。图2表示LM、NM I、NM II和DM在2.0、1.0和0.5时的预测结果。可以看到,在Karlovitz数()足够小(或火焰半径足够大)时,LM、NM I、和NM II的预测值收敛于DM的预测值。在火焰大半径条件下(),可以看到LM、NM I、和NM II的结果与DM的结果几乎相同。因此,未拉伸层流火焰速度()和
图2 不同模型预测的相对于Karlovitz数()的火焰传播速度()函数。
Markstein长度()的精确值可由LM、NM I、和NM II预测。当时,可以看到LM、NM I、和NM II的预测值在所有考虑的Karlovitz数范围内都与DM接近,而在2.0和0.5时LM、NM I、和NM II的预测值与DM有较大差异,尤其是在Karlovitz数很大时。这是由于,在大Karlovitz数条件下,当Lewis数显著不等于1时,被拉伸、未拉伸火焰速度间的相对偏差可超过20%(即),如图2a和c所示。其结果是,用于推导LM、NM I、和NM II的条件不再严格满足。根据DM,在和条件下,火焰速度与Karlovitz数呈非线性相关。因此,像Kelley和Law[26]建议的那样,非线性模型应当在混合气体Lewis数显著不等于1时使用。此外,可以看到NM I和NM II的精度依赖于Lewis数:时NM I比NM II更接近于DM,时NM II比NM I更接近于DM。
为了数值化表示LM、NM I、和NM II的精度,这些模型的误差得到了研究。由等式(6a-c)可得出,LM、NM I、和NM II的误差分别为、和,此处的和来自于DM的精确解,是精确的Markstein长度。以为自变量的误差绝对值函数如图3所
全文共19555字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[9396],资料为PDF文档或Word文档,PDF文档可免费转换为Word


