
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
喷气起动发动机凸轮轴驱动充气阀的设计方法
Michael Moser* Christoph Voser* Christopher Onder*
Lino Guzzella*
摘要:怠速能耗损失占内燃机燃料消耗量的很大一部分。因此,在怠速阶段关闭发动机可以提高整体效率。为了使驾驶员能够接受,必须保证发动机能够快速重起。发动机快速起动可以使用一个强大的电起动器和一个合适的电池来实现,例如在混合动力电动车辆中所使用的。但是,这会造成额外的成本和重量。另一种方法是使用储存在储气罐中的加压空气,该储气罐可以直接喷射气体到气缸中以启动发动机。本文论述了气动发动机启动时使用凸轮轴驱动的充气阀的设计方法。介绍了最佳充气阀设计的一般方法,它可以解决各种要求。提出的设计方法基于代表气动发动机操作的过程模型。展示了双缸发动机的设计实例,并通过试验台实验对得到的优化气动起动进行了实验验证。使用初试压力为10bar的储气罐,发动机的空转速度可以在350毫秒内达到1200转/分钟。
关键词:发动机起动,车辆启动,气动启动,压缩空气,充气阀,发动机停止
一,简介
内燃机(ICE)的固有特性是它们在最低转速下的可操作性有限。起动发动机意味着将曲轴加速至发动机能够正常运行的速度。由于较大的转动惯量和低启动功率,内燃机传统启动需要1秒钟。如此长的起动时使得驾驶员不会接受怠速阶段发动机熄火。因此,传统的内燃机在怠速阶段通常不会关闭。然而,空转损失占总燃料消耗量的很大一部分。在欧洲续航测试工况下(NEDC),如Deacute;onitz等人所示,对于2升自然吸气式汽油发动机,它们会达到6%。(2009年)。为了在满足驾驶员需求的同时消除怠速阶段来利用这种节省燃料的潜力,需要减少发动机启动的持续时间。
减少发动机启动时间的常用方法是安装强大的电启动器(ES)和合适的电池。这种策略可以用于混合动力电动汽车,因为它们配备比传统发动机更强大的电动机和电池。但是,它们会导致额外的重量和成本。 Fesefeldt和Muller(2009)表明,对于这种设置,可以实现在300ms内启动。
Kramer(2005)和Kulzer等人(2006)研究了一种快速启动直喷式汽油发动机的方法。这个想法背后的方法是停止向发动机喷射燃料。如果发动机已停在适当的位置,则可以在静止状态下点燃燃油,以在不使用起动机的情况下重新起动发动机。然而,必须强制发动机停机在适当的位置。解决在所有运行条件下的稳定性和由于发动机低速度下的不完全燃烧而产生的排放物是这种方法的关键问题。 Fesefeldt和Muller(2009)将调查扩展到启动机辅助发动机起动,以减少起动时间和排放。
解决成本和重量问题的有效替代方案是使用可直接注入气缸的压缩空气。压缩空气储存在气罐中,并在膨胀冲程中喷射,产生正向扭矩,加速发动机。发动机纯粹气动驱动,不燃烧燃料。 Vasile等人(2009)研究了气动发动机启动时使用全变量电液阀系统(EHVS)来驱动充气阀(CV)。使用这种设置,升程曲线可以在周期到周期的基础上进行调整。但是,全变量电液阀系统增加了系统的复杂性和成本。图1显示了该引擎设置的示意图。这项工作的目标是在发动机启动时间的限制下优化充气筏设计以实现最小空气消耗。
本文的结构如下:第2节介绍了发动机的型号和设置,以及优化充气筏设计的边界条件。 此外,还提出了一种发动机停止策略。 在第3节中,设计问题被表述为约束最小化问题。 介绍了解决这个优化问题的设计方法。 第4节显示了这种方法在设计实例中的应用,其结果在实验台引擎上通过实验验证。 本文最后总结了这项工作的贡献。
2.模型和设置
为了确定最佳充气筏参数a,使用引擎的过程模型来模拟启动。有关该模型的详细说明,请参阅附录A.本节涉及电动起动器,电起动器气门升程曲线的参数和初始的作用发动机位置。请注意,对于曲柄角phi;= 0°,活塞位于上死点(TDC)之后。
2.1电起动器
与Vasile等人相反,本文重点介绍CSD 充气筏。 在这样的方法中,气门升程曲线是固定的。 此外,阀门只能由旋转的发动机驱动。 对于充气筏的初始启动以及Kramer(2005)描述的其他原因,电启动器是必不可少的。此外,电启动器有助于缩短起动时间,因为它是气动发动机起动期间的额外扭矩提供者。
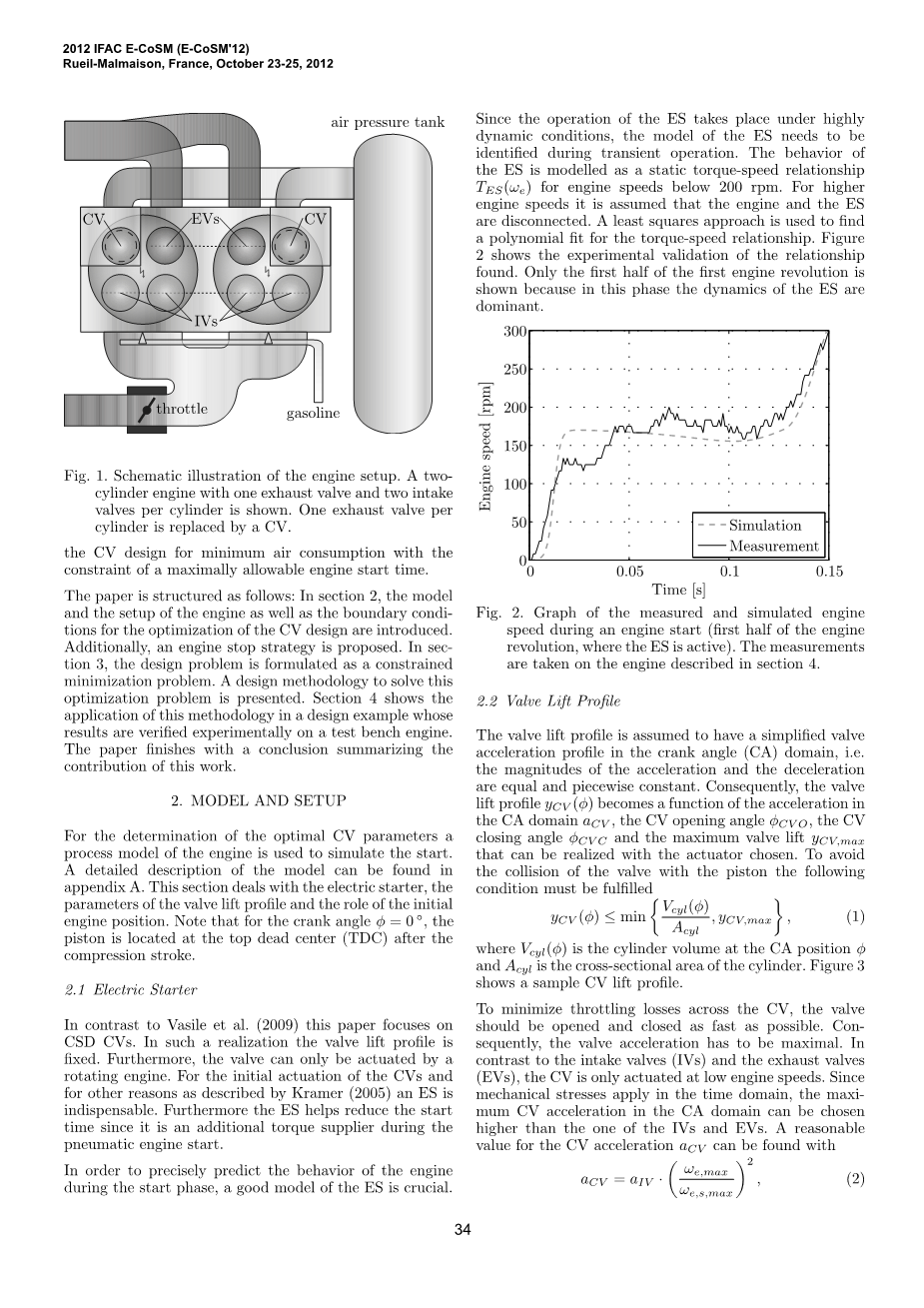
为了精确预测发动机的行为,由于电启动器的运行发生在高度动态条件下,所以电启动器的模型需要在瞬态运行期间被识别。发动机转速低于200 rpm时,电启动器的行为建模为静态扭矩 - 转速关系TES(omega;e)。对于更高的发动机转速,假定发动机和电启动器断开。使用最小二乘法来找出适用于扭矩 - 速度关系的多项式。 图2显示了发现的关系的实验验证,只显示了第一台发动机转速的前半部分,因为在这个阶段,电启动器的动力是占主导地位的。
图2.在发动机启动期间(发动机转速的前半部分,电启动器处于活动状态)测得的和模拟的发动机转速曲线图。 测量是在第4节中描述的发动机上进行的。
2.2气门升程曲线
假设气门升程曲线在曲柄角(CA)范围内具有简化的气门加速度曲线,即加速度和减速度的大小相等且分段恒定。 因此,气门升程曲线yCV(phi;)变成CA区域中的加速度aCV,充气阀打开角度phi;CVO,充气阀闭合角度phi;CVC和可以用致动器实现的最大气门升程yCV,max的函数选择。 为避免阀门与活塞碰撞,必须满足以下条件yCV (phi;) le; Vcyl(phi;)Acyl。
其中Vcyl(phi;)是CA位置phi;处的汽缸体积,而Acyl是圆柱体的横截面积。 图3显示了一个样品充气阀升程曲线。
为了尽量减少整个充气阀的节流损失,应尽可能快地打开和关闭阀门。 因此,阀门加速度必须达到最大。 与进气门(IVs)和排气门(EVs)相反,充气阀只在发动机低速度时启动。 由于机械应力在时间域中应用,所以CA域中的最大充气阀加速度可以选择为高于IV和EV中的最大充气阀加速度。 可以找到充气阀加速度aC的合理值。
图3. 充气阀升程曲线示例。 负曲柄角表示上死点之前的位置,而正曲柄角表示上死点之后的位置。
其中aIV表示CA域中的IV加速度,omega;e,max是最大发动机转速,而omega;e,s,max是气动启动操作期间最大可允许的发动机转速。给定最大升程和阀门加速度,充气阀升程曲线的其余参数为phi;CVO和phi;CVC。 第3节介绍了找到合适值的方法。
2.3发动机初始位置
气动发动机起动的持续时间明显依赖于首次注入压缩空气所经过的时间。越早注入加压空气,发动机启动得越快。直至充气阀开启于phi;CVO的持续时间主要受电启动器尺寸和初始发动机位置phi;0的影响。因此,发动机应该关闭,以使活塞处于压缩冲程接近充气阀打开角度。静止位置会受到发动机关闭期间油门启动的影响。为了找到模型中初始发动机位置的适当值,进行了几个实验。执行多次发动机关闭并持续节气门开启,并记录其余位置。图4显示了双缸双引擎的结果(参见第4节)。节气门开度为2%时可获得最佳性能,因为方差最小,平均位置最靠近上死点。较高的值产生一个更远离上死点的休息位置。较小的节流阀开度值会导致其余的重复性差位置,这是不可取的。因此,选择上死点(bTDC)之前的初始位置phi;0= 95°CA。
2.4发动机起动过程中的油门控制
请注意,发现的节气门位置设置仅在发动机关闭期间相关。 如Vasile等人所示。 (2009),在发动机启动阶段完全关闭节气门使空气和时间最优。 关闭节气门意味着进气歧管压力在启动过程中下降。 因此,压缩工作减少了。 因此,对于后续的设计方法,节流阀始终假定为完全关闭。
图4.在发动机停机期间测量的各种节气门开口的发动机静止位置。 有关引擎的详细信息,请参阅第4节。
3.设计方法
在本节中,阐述了充气阀设计的基础优化问题。对优化问题进行分析和讨论。介绍了其解决方案的过程。确定满足所有约束条件的可行集合,并引入具体的设计选择。提出的设计方法的目标是找到设计变量的值,其使得发动机能够在小于规定的起动时间tsmax内达到规定的起动速度omega;e,并且同时使加压空气的量是最小的。相关的设计变量是:
phi;CVO:充气阀开口角度,phi;CVC:充气阀关闭角度,dCV:充气阀直径。
令Delta;=phi;CVO,phi;CVC,dCV R R R 为考虑相关设计变量的参数空间。开始时间和空气消耗量也取决于初始罐压pt。在驱动循环中发动机运行期间,罐压力变化。完全可变的阀门可以调整阀门正时,以适应不断变化的气罐压力。但是,CSD 充气阀的气门正时是固定的。因此,设计程序必须考虑气罐压力的整个工作范围。为此,使n个不同的罐压ptisin;Rn产生的空气消耗的加权总和被最小化。标量加权函数w(pt)0仅取决于初始罐压。 它用于选择优化中的特定初始罐压力。w(pt)的合理选择是在低初始罐压下使其变大。
图5.气动发动机起动时的发动机转速和累积耗气量。 在恒速阶段,发动机仅由电启动器驱动
3.1优化问题的性质
由于发动机的往复行为和高度非线性的过程模型,优化问题具有特殊的特征。 这些在下面讨论。
可行集合定义为Omega;(pt):= {Delta;| ts(Delta;,pt)le;ts,max},(7)即满足初始罐压pt的性能约束的所有设计。 最小的初始气罐 Omega;(pt)不为空的最小初始储气罐压力定义为可行集合的最小储气罐压力~pt,Omega;。考虑气罐压力必须满足pt(i)ge;p〜t。然而,由于最低的罐压是先验未知的,所以选择pt很困难。这一事实使得制定合理的加权函数w(pt)也变得困难,从而促使选择正确的罐压力范围。此外,发动机的往复行为是解决最优化问题的另一困难。函数[ma,ts] = fPM在空气质量和开始时间内都是分段连续的。通过引入以下考虑显示了这一事实。设delta;1和delta;2是两个设计参数,其中kdelta;1 - delta;2kinfin;lt;?其中k∙kinfin;表示无穷范数和 gt; 0是一个非常小的数字。因此,这两种设计仅略有不同。然而,对于delta;1和delta;2的具体选择,相同初始罐压的fPM(delta;i,pt)的评估将产生完全不同的结果。当在不同数量的动力中达到omega;e,s时发生:Nps(delta;1)6 = Nps(delta;2)。因此,在delta;1和delta;2之间ma和ts存在不连续性。目标函数中的不连续性会导致数值优化算法出现问题。
3.2优化问题的解决方案
根据目标和先验知识,提出了两种求解方法,即数值优化和蛮力方法。为了数值优化,提出了粒子群优化(PSO),因为它与前面描述的问题的特性很好地吻合。如果已知最小罐压力以便合理选择pt,则数值优化是适合的。最佳解决方案的推导速度相当快,并找到了精确的解决方案。在蛮力方法中,过程模型可以模拟多种充气阀设计变量和罐压。这在计算上要求更高。当然,这取决于所考虑的网格的粗糙程度。该方法的优点在于不需要知道最小罐压。它是从方法中导出的。此外,仿真结果可用于灵敏度分析。解决方案的精度受到网格粗糙度的限制。过程模型的评估在该步骤中,评估非线性过程模型,即13,872个模型评估。确定可行集合及其最小初始罐压对模拟结果的分析产生的最小初始罐压为~pt,Omega;asymp;9.2 bar。图7显示了这个结果。它显示了dCV和pt的固定组合所能达到的最小开始时间。 350 ms线表示pt-dCV子空间中可行集合的边界。所有初始油箱压力和充气阀直径组合的tsle;350 ms是可行集合的一部分。在测试台上安装直径为dCV = 19 mm的充气阀。因此,该直径是为设计示例选择的,并在整个优化过程的其余部分保持为固定值。气罐压力范围和加权函数的定义根据图7所示的数据,气罐压力矢量pt可以被定义。在这个例子中,只考虑一个靠近可行域边界的储罐压力。
图7.各种CV直径和初始罐压的最小开始时间。
4.1讨论
优化程序产生上死点后的充气阀开启角度,这个结果是有利的,因为如果充气阀在上死点之前打开并且初始罐压力大,即明显大于上死点处的缸内压力,则第一发动机转速将变得关键。 在那种情况下,在活塞通过上死点之前,通过喷射加压空气会产生负转矩。 如果该扭矩超过ES产生的扭矩,则发动机不能气动启动。 图8清楚地表明,关于空气消耗,充气阀的后期关闭是不利的。 这个事实的原因是EV的开放角度是114°CA aTDC。有一种设计,其中phi;CVCgt; 114°CA aTDC意味着加压空气直接从充气阀流入排气歧管。 这样的设计增加了空气消耗量,而不会产生显着更大的扭矩。
图8. dCV = 19 mm和pt = 10 bar的各种充气阀开闭角的加压空气消耗量。 黑线表示可行域的边界。 标签EVO表示EV开启角度。 黑圈:最小空气消耗量。 灰色三角形:最大耗气量。
灵敏度分析基于图7,8和9所示的结果,可以对集合Gamma;中的参数进行灵敏度分析。图7显示,对于小的充气阀直径,满足tsle;ts,max的最小罐压显著增加。对于小型dCV,由于流量限制,可以通过充气阀传输更少的空气。因此,扭矩较小。增加的流量限制需要通过更高的密度来补偿,即更高的罐压力。对于dCVgt; 14 mm,固定罐压力的启动时间几乎是恒定的。人们会认为更高的dCV值会导致更多的空气被传输,从而缩短启动时间。但是,有一个抵消效应。对于较大的阀门直径,在充气阀打开后,罐体和缸体之间的压差迅速减小。这种效果导致质量流量的减少。图9显示了对于固定的pt = 10 bar和dCV = 19 mm,phi;CVO和phi;CVC的各种组合的开始时间。最大开始时间等于370毫秒,由灰色三角表示。最小开始时间为341毫秒,由黑色圆圈表示。因此,最大开始时间比最小开始时间高8%,这表明灵敏度相当小。在上死点周围,开始时间ts对于变化的充气阀角度几乎是恒定的。另一方面,开始时间可以通过以后关闭来减少。图8所示的空气消耗显示了对充气阀定时的相当高的灵敏度。在
全文共7214字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[9363],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


