玻璃形成液的粘度外文翻译资料

 2022-07-17 14:37:13

英语原文共 5 页，剩余内容已隐藏，支付完成后下载完整资料

玻璃形成液的粘度

John C. Mauroa，Yuanzheng Yueb，Adam J. Ellisona, Prabhat K. Guptac, and Douglas C. Allana

a康宁公司科学技术部，康宁，NY 14831；b奥尔堡大学大学化学部，奥尔堡，丹麦，DK-9000；以及c俄亥俄州立大学材料科学与工程部,哥伦布，OH 43210

2009年10月9日，J.C.Phillips，罗格斯大学，峰会，NJ（2009年6月15日接收）

超粘性液体的低温动力学是理解玻璃转变和松弛现象的关键，包括（可能存在的）理想的热动力学玻璃转变。但是现有的粘度模型，比如VFT和AM方程在对低温粘度进行推算会出现系统误差。我们提出了一个改进的描述温度与粘度关系的模型，这个模型中有机和无机液体使用相同的参数。这个模型有明确的基于构型熵的温度依赖性的物理基础，在有限的温度下它还对低温等粘线提供了准确的预测。我们的研究结果对kauzmann熵变以及与之相关的理想玻璃转变表示怀疑。

过冷液最有趣的特点就是当它冷却至玻璃转变时其粘度的急剧上升，这种急剧的超阿伦尼乌斯升伴随着能通过典型衍射实验几乎观察不到的变化，这里有几个问题：

  1. 这种行为是否具有普遍性？
  2. 在低于玻璃转变温度下的一个有限温度范围内玻璃的粘度是否偏移？
  3. 是否存在一个热力学机奇点引起了粘度的急剧上升？

这些问题是解释过冷液体行为的关键。由于玻璃转变时长程结构的松弛时间，所以平均粘度的测量无法再低于玻璃转变温度测量。找到一个能最好描述粘度与温度关系的模型对于研究是很重要的，这个模型的拟合参数最少两个。描述一个简单的阿伦尼乌斯模型需要两个参数，而super-Arrhenius的行为模型最少要三个参数。在最经济的条件下，我们采用三个参数的模型来描述过冷液体的粘度。

最流行的模型是VFT模型：

公式中T表示温度，X表示组成，三个VFT参数（eta;、A、T）是通过拟合公式1得到的，用来测量粘度的数据。在高分子科学领域，公式1也被称为WLF方程，尽管VFT在应用到多种液体的计算上有显著的成功。但是在低温的研究出现了问题。另一个成功的三参量方程是AM方程，这是基于原子跳跃法推导的方程：

，。这3个也是拟合参数，在Avramov和Milvhev的研究之前已经有几个科学家提出了公式2.尽管另一个三参数模型最近由Elmatad等人提出，这种二次形式的方程只能在一个狭窄的温度范围内有效，过高或者过低的温度都不适用。现在我们只研究VFT和AM的模型，这两种模型使用单一的三参数形式，适用于所有的温度。

模型，我们用亚当-吉布斯方程回顾一下粘性液体的动力学问题，将

粘度与液体的构型熵联系起来：

这个方程在描述系统的各种松弛行为方面取得了显著的成果，并且它

为过冷液体非均匀成核动力学提供关键因素。B（x）通常是作为拟合

参数，是一个高效的激活势垒。构型熵Sc（T,X）在玻璃系统中比较

复杂，但是可以通过约束理论将其模型化。（约束理论是一个比较普

遍的理论用于研究热玻璃的热动力学，特别是在玻璃转变温度附

近 ）。基于Naumis的能量分析和GUPTA以及Mauro的温度依赖约束

模型，构型熵可以与拓扑结构的每个自由原子关联。

N表示原子数，k是玻尔兹曼常数 ，Omega;是每个floppy模式下的退化

构型的数量为了得到最好的模型，考虑一个简单的两态系统，在这个

系统 中网络结构互相联系或者破坏，能量差表示为

在高温条件下，公式5 每个自由原子有 3个自由度，绝对零度时网

络结构不动，

f（0，x）=0，骨架结构不会被破坏。定义k（x）=B（x）/3NklnOmega;，

C（x）=H（x）/k，可以得到三参数粘度模型

公式6是由Waterton在1932年提出的几个经验公式中的 一个，但是后续进展 我们并不 了解。尽管公式6可以通过在Arrhenius粘度公式中假设一个势垒，但是这在物理上是不现实的，第一因为势垒在绝对零度的时候是无限大。第二高温动力学是由熵效应主导，而不是一个简单的激活势垒模型。基于 约束的方法得到一个构型熵的物理现实性公式6。

尽管公式1，2和6的粘度模型有不同的参数，每一个模型都可以改写出相同的物理意义量：第一 ，玻璃转变温度Tg（x）；第二，强弱性，m（x）；第三，外推无限温度粘度，（x）。对于任何成分的x，玻璃化转变温度定义为剪切粘度为1012pa-s，强弱性定义为

有了这些定义，VFT的公式1可以写为公式8

AM的公式2可以表示为 公式 9

公式6可以改写为公式10

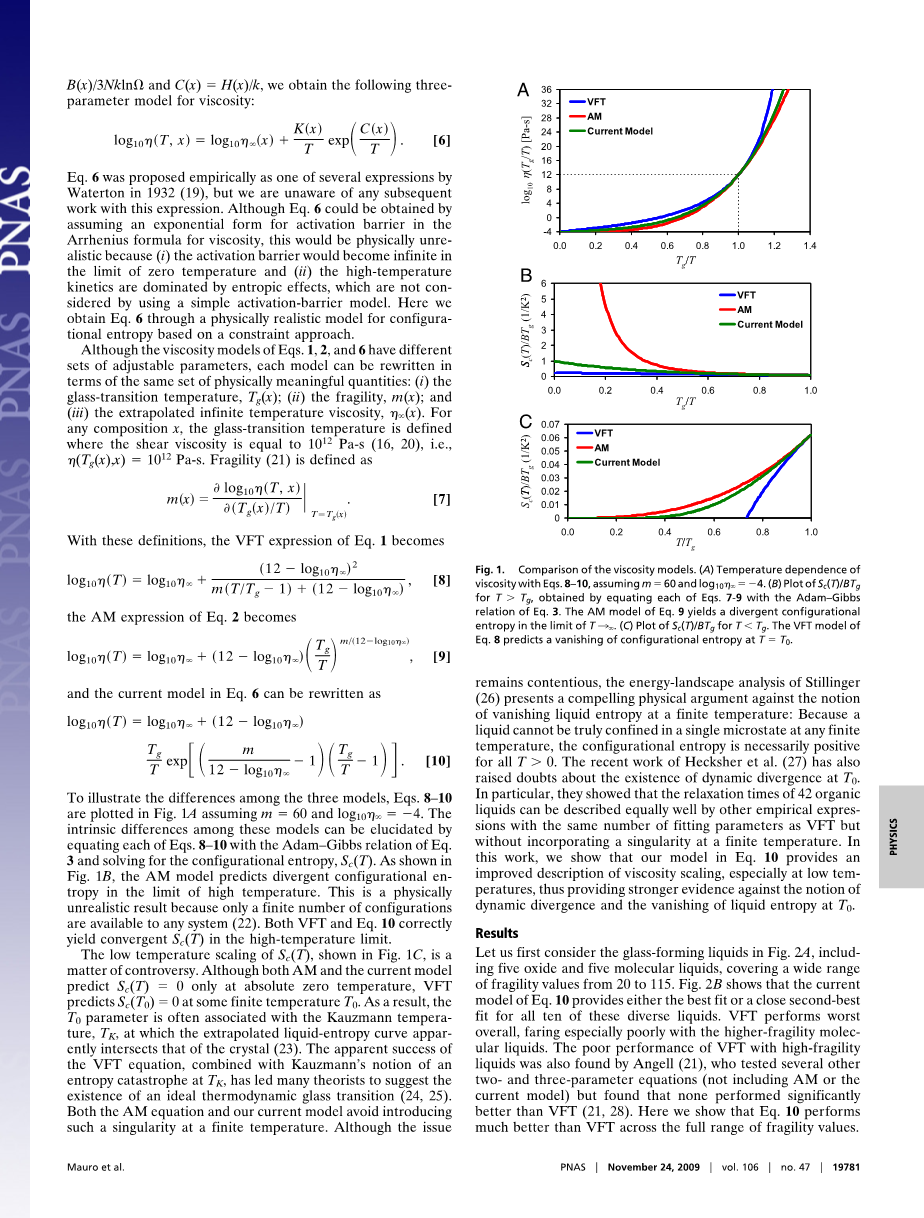
为了解释三种模型的不同，公式8-10绘制在图1A中，假设m=60，

log10 =-4。这些模型之前的内在差异可以通过公式8-10以及吉布斯自由能公式和构型熵来阐明。在图1B中，AM模型可以预测高温下的构型熵。这在物理上是不现实的结果，以为系统的构型熵是一个有限值。VFT和公式10在计算高温条件下的粘度有错误。

图1.粘度模型的比较，（A）公式8-10的粘度温度关系假设m=60 log10=-4

  1. 在Tgt;Tg的时候，Sc（T）/B的曲线图，利用公式7-9和吉布斯公式3，AM模型在外推温度趋向无穷时有奇点。
  2. Sc（T）/BTg在Tlt;Tg的情况下，VFT模型的公式8预测T=To会出现构型熵消失的情况。

低温下的Sc（T）在图1C中，有矛盾的图。尽管AM和现在的模

型可以预测在绝对零度下Sc（T）=0，VFT模型预测在一些有限温度下Sc（T）=0。所以T0参数一般都是与Kauzmann温度 Tk联系起来，外推的液体熵曲线与晶体关联。VFT方程的成功在于结合Kauzmann的熵变温度Tk的概念，使得许多理论学家去研究理想热力学玻璃转变。尽管这个问题依旧存在疑问，Stillinge的能带分析得出的结果与液体熵在有限温度下为零的观点矛盾。因为液体在任何有限温度下都不能单独限制，在Tgt;0的时候，构型熵与温度是严格正相关的。Hecksher近期的工作结果也对T0时候的动力学上的偏移存在表示怀疑。更重要的是，他们发现42种有机液体的松弛时间可以被其他经验公式完美的描述，而这个公式使用和VFT公式相同数量的拟合参数，但是在有限温度下不出现奇点。公式10我们阐释这个观点，它对粘度有一个更精确的描述，特别是在低温情况下。对动力学偏移及T0时候液体熵的消失提出疑问。

结论

首先考虑表2A中的玻璃形成液，其中包括5种氧化物和5种分子组成液，强弱性值从20到115。图2B给出的是公式10的模型，它是最合适的计算模型。VFT

方程的吻合度是最差的，特别是针对弱熔体的计算十分差。Angell

同样也发现

了VFT方程在弱熔体方面的不适用，他同样也测试其他两参数和三参

数方程（不包括AM和现在的模型），结果表示VFT的表现最明显。

在所有的强弱性值范围内，公式10比VFT方程更为适用。

图2.（A）5种氧化物和有机液体的粘度，包括了脆性值在20-15范围。

（B）模型8-10的均方根误差。AM公式的拟合图在图2B，相对来说其拟合的比较好，但是在非物理性外推高温下表现不太好。在无限高温的条件下松弛时间是10-14s，与轰击势垒和结构重排的时间对应。硅酸盐的剪切模量Ginfin;=29GPa，麦克斯韦方程结果为Gasymp;10-3.pa-s。因为分子液的G比较低，所以外推粘度的计算值应该比分子液低。同时，硅的应该更低，因为强弱转变。在图3A中，由AM方程得出的结果偏高，符合图1B中其构型熵的非物理偏差。Hecksher以及Yue的研究表明，在一个物理现实值得情况下，AM方程的适用度明显比AFT方程更差。

接下来我们通过康宁公司组成研究来考虑568种不同的硅酸盐液，这些液体包含了很大的组成范围，从简单的钙铝硼酸盐到复杂的多达11种氧化物成分的液体。每一个组成由在10-106pa-s范围内的6-13个数据点表示，这些数据是通过旋转主轴的方式获得。有85种组成是在106.6pa-s以及1011pa-s的数据表。等粘线温度的测量精确度为plusmn;1K。拟合所有的粘度数据，公式10的计算结果误差为0.0347而VFT方程的误差是0.0350,AM方程误差是0.0470。在图3B中可以看出，现在的公式计算值得误差最小，在给定的无穷远温度的限度参数下，当前公式更适用。原子之间的相互关系不在重要，因为系统是由动能主导了。我们注意到暗示了高温及线下简单的松弛。在图3B中，AM模型对几乎所有康宁公司的组成计算得出了不科学的高数值。

图 3外推无限温度下的粘度

  1. 组分x的分布在图2
  2. 568种不同组成x分布的直方图

当前的模型预测的误差值很小

在玻璃转变温度附近，高分子玻璃会开始形成大的集群或者结晶。然而在低温下的表现与玻璃网络数据符合，在这种情况下结晶化很难。为了研究低温下的粘度变化，我们利用外推法测试了康宁公司的85种组成，包括106.6和1011pa-s的数据。在图4A中，这3种粘度模型都只是在高温下符合。利用推断法预测低温下1011pa-s的等粘线温度，预测的错误结果在图4B-D中，VFT模型和AM模型都有系统性的误差。AM模型曲率太在1011pa-s的等粘线温度下偏小大约5.6K。相反的，VFT模型的曲率太大，在1011pa-s的等粘线温度下偏大约9.4k。VFT模型在T0时候的动力学假设错误导致了系统的偏差，以至于低温时粘度上升过于陡峭。在图4D中，当前的粘度模型在低温下没有这种偏差，它的误差在0.5k左右。

图4，低温外推温度的测试

  1. 低温外推温度测试，适用于高温粘度数据测试并且预测1011pa-s等粘线温度
  2. 在预测1011pa-s下85种康宁等粘线出错了。水平轴上的误差按递减的顺序排列，轴上给定的位置对应三种不同的液体。
  3. 等粘线温度的均方根误差适用三种不同模型。
  4. 等粘线温度平均误差。

讨论

公式10的推断能力为在有限温度下动力学发散以及构型熵的消失提

供了论点，也是支持Simon等人低温试验的观点。我们的研究结果也

对二级转变的温度T2相对的T0和Tk的存在提出疑问，根据吉布斯

方程，构型熵会在温度为T2时消失，并且液体和玻璃的热容在Tg时

也存在差异。吉布斯方程的另一个问题在于高温下的发散。值得注意

的是，尽管我们当前的公式是基于吉布斯在热动力学和动能的关系，

但是并不依赖于Adam和Gibbs讨论的理想玻璃转变的Sc。

公式8-10中，只有当前的公式提供了高温和低温限度下的构型

熵的推断法。所以，公式10给的存在提供了物理意义，同时也能更加精确的描述低温下的粘度。VFT模型以及AM模型的失败之处在于尺寸效应的限制，这在复杂系统中是很普遍的。在高温限度下，剪切可以描述为单个原子的行为。当温度更低时，剪切流动的重排长度范围有所增加。这种尺寸效应是理解其他过冷液体和玻璃的关键，比如拉伸松弛指数以及动力学非均匀性。从更一般的角度看，我们必须在研究复杂系统和玻璃形成系统方面有更多基础性的想法，才能在高温和低温下对粘度的测量有更精确的数值。感兴趣的读者可以浏览最近Naumis和Cocho的文章。建立在多尺度的概念上，这些作者提供了一个较好的N/D规则，这个原则可以适用多成分的分析。归功于多尺度效应，对于玻璃系统中N（分子）和D（分母）不在需要多项式表示了。

公式10在低温下测量精确度的提高，结合其在有限温度下的奇

点有力的推翻了动力学发散和玻璃形成液存在的观点。过冷液的任何现实模型以及玻璃态必须考虑正确的热力学和动力学。Stillinger的能带模型中有一个特别令人信服的方法。目前的研究仅仅是平衡液的粘度，由Mauro等人将粘度的研究拓展到1016pa-s，并且提供了一套完全理论和经验用来分析非平衡态玻璃的粘度，包括Arrhenius在玻璃转变温度下的研究。

参考文献：

  1. Sturm VKG(1980)On the temperature dependence of viscosityof liquids (Translated from German).Glastechn Ber 53:63–

    全文共10946字，剩余内容已隐藏，支付完成后下载完整资料

    资料编号：[9266]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章