
英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
土壤泥浆的固结特性——来自水力固结试验
作者:Patrick J.Fox:ASCE准成员[1];Christopher D.P.Baxter[2]:ASCE学生会员
【摘要】有限应变固结理论通常用于高压缩性废料(如磷粘土、废渣和尾矿)处置设施的初始设计和后期回收。本文提出了一种替代性的方法来进行水力固结试验,以测量所需的压缩性和导水性本构关系。此外,本文导出了定常流动条件下,水工固结试验的泄流速度、总压头、孔隙水压力和有效应力分布的封闭式方程,并介绍了一种两阶段试验方法,即在两个连续的水力梯度上测量试件高度和泄流速度。在第二阶段结束时,通过切片得到局部孔隙比的分布。与其他可用方法相比,试验结果分析具有优势,因为不需要专门的数值程序来计算土样所需的本构关系。该模型的理论预测与两种粘土浆的水工固结试验结果吻合较好。
引言
Imai(1979)提出了一种新的固结试验,称为“水力固结试验”,用于测量软土的压缩性和水力传导率本构关系。原则上,水力固结试验(也称为“渗流诱发固结试验”)是通过在刚性壁固结仪中对土壤样本施加向下的水力梯度来进行的。渗透力使土壤固结,并在试件内产生不均匀的有效应力分布。一旦达到稳定的流动条件,使用从下方插入试样的针头测量局部孔隙压力。稳定状态下的孔隙比分布由从单元中取出试样后切片获得的局部含水量测量值确定。根据这些测量结果,孔隙比、垂直导水率、体积变化系数和固结系数的关系可作为垂直有效应力的函数。
与测量泥浆和其他高压缩性土壤材料特性的其他可用试验方法相比,水力固结试验具有许多优点:(1)压缩性和水力传导率的关系是从一个单一的测试获得的;(2)得到了单个水力梯度的关系式;(3)直接测量关系,无需对试验结果进行理论解释;(4)该试验非常适合在低有效应力范围内进行测量。因此,水力固结试验通常可以缩短高压缩性材料的总试验时间。长时间要求已被确定为传统泥浆固结试验的主要缺点,试验需要几个月或更长时间才能完成(Carrier等人,1983年)。
Imai(1979)最初提出的试验程序也有缺点:(1)要求有一个专用的实验装置,能够测量流动过程中试件内部的局部孔隙压力;(2)试验结束时必须将试样切片,以测量局部含水量;(3)试验结果可能因固结计壁上形成流道而失效(即“侧壁泄漏”)。如果试样顶部的有效应力为零,则侧壁泄漏尤其有问题,通常可以通过在进行试验之前对试样施加超载荷载来避免。同样,在试验结束时测量局部含水量相当简单,不会对该方法的使用造成严重限制。另一方面,在稳定流动期间,可靠地测量试样内部不同高度的局部孔隙压力是一项困难的任务,需要高度发达的实验技术(Baxter,1994)。因此,由于这一局限性,水工固结试验在实践中并没有得到广泛的应用。
高压缩性废料(如磷质粘土、废渣、尾矿、泥浆和淤泥)的经济和环境安全处理重新引起了人们对水力固结试验的兴趣。这些材料处置设施的成功规划、设计、运行和后期回收需要对沉降和超孔隙压力进行可靠的预测,作为时间的函数。大量研究表明,有限应变固结理论是进行此类预测的有用工具(Caldwell et al.1984;Schiffman et al.1984;Scully et al.1984;McVay et al.1986;Townsend and McVay 1990)。然而,正如Krizek和Somogyi(1984)、Feldkamp(1989)和Toorman(1996)所讨论的,有限应变固结模型成功应用的最大障碍可能是需要准确说明土壤材料特性。泥浆和其他高含水量土壤所需的压缩性和导水率关系的测量尤其具有挑战性,因为相关的有效应力范围低、应变大、抗剪强度非常低,并且典型的固结过程很长。因此,最近提出了水力固结的概念,作为方便测量高压缩性废料本构关系的方法(Huerta等人,1988年;Abu Hejleh等人,1996年)。
为了避免Imai(1979)原始试验的一些缺点,Huerta等人(1988)提出了对水力固结试验程序的修改和一种新的分析技术来解释结果。通过假设压缩性和水力传导率本构关系的数学形式可以用幂函数表示,Huerta等人(1988)避免了在土样中进行局部孔隙压力和孔隙比测量的需要。为了获得一个独特的解决方案,需要稳态流速,并且在试验完成后必须测量试样底部的孔隙比。AbuHejleh等人(1996年)最近提出了一种水力固结试验的替代试验和分析程序。实验过程分为三个阶段:(1)测量零有效应力孔隙比;(2)在稳态流动时,测量试样高度和穿过试样的孔隙压力差;(3)在高有效应力下测量后续分步加载增量的导水率和孔隙比。使用此程序,不需要测量局部孔隙压力、局部孔隙比和稳态流量。对于每种方法,测试结果都必须使用特殊的计算机程序进行数值分析,而这些程序通常是执业工程师无法使用的。
本文的目的是提出一种替代的技术来进行水力固结试验和分析结果,以获得压缩性和水力传导率本构关系的土壤泥浆标本。本文介绍了一种两阶段试验方法,即在两个连续的水力梯度上测量试件高度和泄流速度。在第二阶段结束时,通过切片得到局部孔隙比的分布。试验数据的分析用封闭形式的方程表示,因此无需使用数值算法和特殊的计算机程序来计算所需的本构关系。在接下来的部分中,首先介绍了理论模型。利用Imai(1979)的原始试验数据对东京湾淤泥进行了单次水工固结试验,说明了该模型的适用性,介绍了试验过程,并对试验结果进行了分析测试结果的解释。最后,利用粘土浆两阶段水工固结试验数据对该方法进行了说明。
理论
Fox(1996)在实验室提出了水力梯度对实测导水率影响的理论模型。导出了土样等效垂直导水率随土样高度、边界应力条件、压缩性和导水性本构关系的封闭表达式。由于该理论考虑了渗流固结对可压缩介质渗流的影响,因此它同样适用于水力固结试验的解释。对于该应用,包括修改,使得压缩性关系的数学形式不受限制。
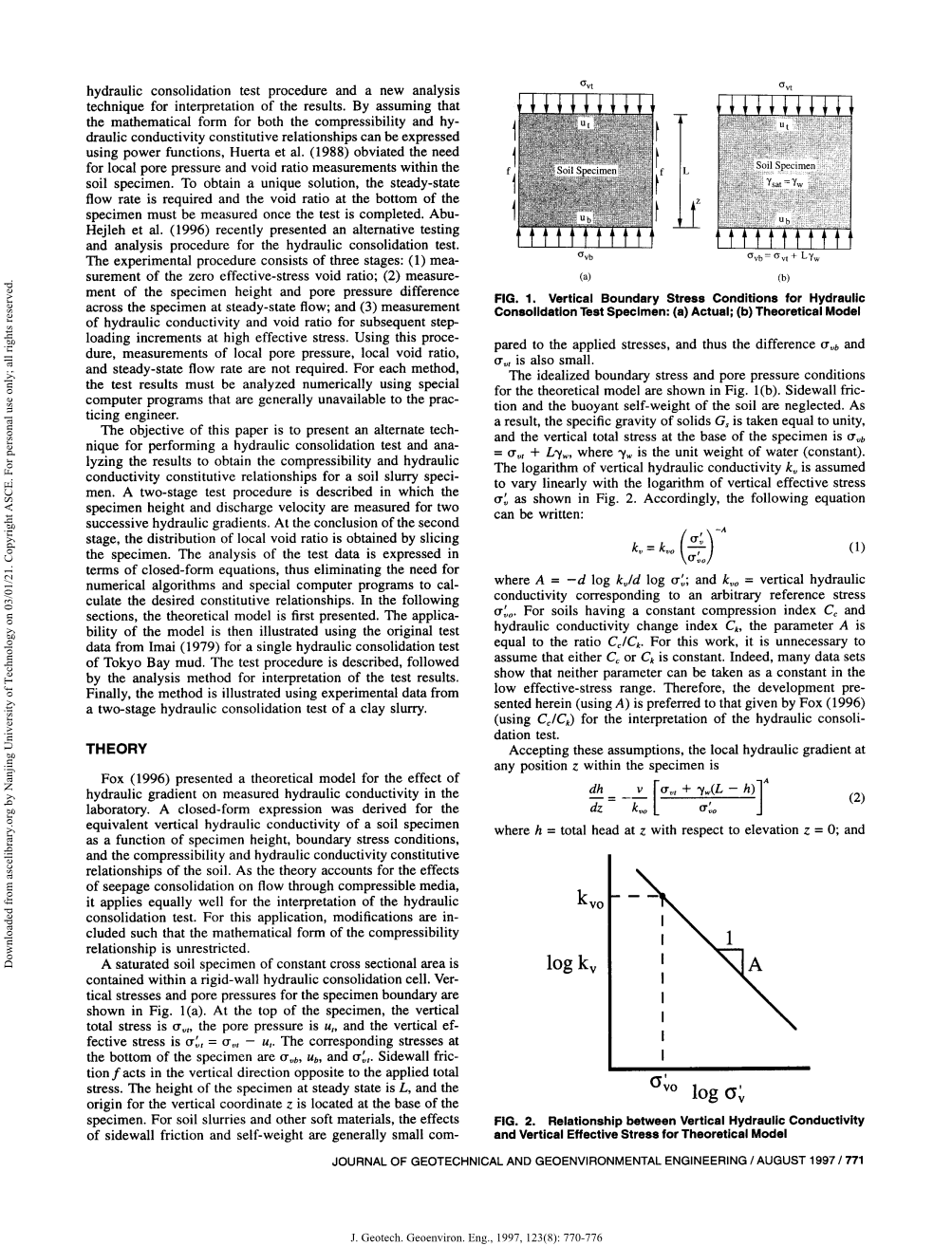
在刚性壁水力固结池中装有等横截面积的饱和土试样。试样边界的垂直应力和孔隙压力如图1(a)所示。在试件顶部,垂直总应力为,孔隙压力为,垂直有效应力为。试样底部的相应应力为、和侧壁摩擦作用于与施加的总应力相反的垂直方向。稳定状态下试样的高度为,垂直坐标的原点位于试样底部。对于泥浆和其他软材料,与施加的应力相比,侧壁摩擦和自重的影响通常较小,因此差异和也较小。
图1.水工固结试件竖向边界应力条件:
- 实际;(b)理论模型
理论模型的理想边界应力和孔隙压力条件如图1(b)所示。侧壁摩擦力和土壤的浮力自重被忽略。因此,固体比重等于1,试样底部的垂直总应力为,其中是水的单位重量(常数)。假设垂直导水率的对数与垂直有效应力的对数呈线性变化,如图2所示。因此,可以写出以下等式:
(1)
其中;=对应于任意参考应力的垂直导水率对于具有恒定压缩指数和导水率变化指数的土壤,参数等于比率对于本工作,无需假设或是恒定的。事实上,许多数据集表明,在低有效应力范围内,两个参数都不能作为常数。因此,对于液压控制台试验的解释,本文提出的开发方案(使用)优于Fox(1996)(使用)给出的开发方案。
接受这些假设,试件内任何位置的局部水力梯度为:
(2)
其中相对于标高的处的总水头;稳态下的放电速度。正对应于正方向的向上流动。
图2.理论模型中垂向导水率与垂向有效应力的关系
对于的一般情况,(2)的解是:
(3)
其中积分常数。使用试样顶部和底部的边界条件:
(4,5)
公式(3)简化为稳态下总水头分布的以下非线性表达式:
(6)
在任何垂直位置,是,试样高度和顶部和底部边界应力条件的一个函数
从(6)中,可以计算出所有其他感兴趣的量。处的孔隙压力为:
(7)
将(6)代入(7),局部孔隙压力的表达式变为:
(8)
同样,垂直有效应力为:
(9)
稳态放电速度为:
(10)
方程(6)和(8)-(10)适用于。对于的特殊情况,可以导出以下相应的方程式(Fox 1996):
(11)
(12)
(13)
(14)
为了完整起见,这里给出的例子代表了数学分析的一个特殊条件,在实践中通常不需要。因此,本文其余部分的方程的发展将以为假设进行。
上述解析表达式描述了稳定状态下水力固结试件内的流动和应力条件。以封闭形式写出这些解需要以下假设:(1)压缩和流动是一维的;(2)垂直有效应力的对数和垂直导水率的对数之间存在一对一的线性关系;侧壁摩擦力和土体自重对总应力分布的综合影响较小。在无侧壁渗漏的情况下,均质土样的刚性墙水力固结试验满足第一个假设。侧壁泄漏可使用分隔中心的双环底座进行检测。理论模型的适用性通过样品和周向流进行了说明(Daniel 1994)。
对于第二种假设,大量的研究表明,与的线性模型是低有效应力范围内高压缩性土的一个很好的近似。图3显示了10种软土(磷质粘土、疏浚粘土、海洋粘土和高岭石泥浆)的与的曲线图。
图3.10种软土的实测导水率与垂直有效应力的关系(单个数据点按引用文献中的数字缩放)
对于7项研究,数据点根据引用的参考文献中的图10进行缩放。其余三个参考文献(Somogyi等.1984;McVay等.1986;Tan等.1988)将方程与其压缩性和水力传导率数据拟合,这些关系如图3所示。每项研究的结果表明,在有效应力的几个对数周期内,近似为常数。有趣的是,图3的数据落在一个相对较窄的频带内,作为第一近似值,可以用以下线性回归方程来描述:
(15)
常数本构模型,也被用于水力固结和有限应变固结的分析和数值研究(Huerta等.1988;Townsend与McVay 1990)。因此,综上所述,先前研究的结果表明,与的线性关系为许多土壤泥浆提供了令人满意的近似值。
关于第三种假设,Been和Sills(1981)以及Tan等人(1988)发现侧壁摩擦对粘土泥浆自重固结试验的总应力分布几乎没有影响。通过降低试样的高径比、在固结仪壁上涂抹二硫化钼润滑脂以及使用带有聚四氟乙烯涂层壁的固结仪,可以进一步降低侧壁摩擦的影响(Leonards和Girault 1961)。为了得到封闭形式的解,还必须忽略土壤的自重。对于实验室试样,与施加的应力和试样内孔隙压力的相对较大变化相比,与此假设相关的误差通常较小(Znidaricc等人.1986;Fox.1996)。另一方面,在高含水率材料固结沉降的现场预测中,通常不能考虑自重。对于这种预测,需要一个有限应变固结模型来解释固体的浮力(Gibson等.1981;Fox and Berles,in press,1997)。
实验数据
图4.东京湾淤泥的实测导水率与垂直有效应力[来自Imal(1979)图14缩放的单个数据点]
利用Imai(1979)的原始试验数据对东京湾淤泥进行了单次水工固结试验,说明了理论模型的适用性。泥浆试样的初始高度,初始孔隙比。采用恒定水头流量控制系统,在向下的水力梯度下对试样进行固结。在稳态下,试样的测量高度为,放电速度为,边界孔隙压力为,。由于未对试样顶部施加超载,,。图4显示了与从该试验中测得的的函数关系。在双对数图上,数据的趋势几乎是直线,在参考应力下,东京湾泥浆的相应材料性质为和。
图5.测量和估计的分布:(a)超孔隙压力;(b)东京湾淤泥水力固结试验的孔隙比[根据图:《国际人道主义法》(1979年)第9条和第10条]
稳态下测得的超孔隙压力的分布如图5(a)所示。如果局部导水率恒定,则试样上的超孔隙压力分布呈线性。但由于渗流固结作用,实测分布呈高度非线性,局部水力梯度随深度增加而增大。图5(a)还显示了使用(8)获得的超孔隙压力分布的估计值。对于,(1)预测了试样顶部的无限导水率。为了避免这一困难,根据泥浆的初始孔隙比计算的当量值[Huerta等人(1988)和Townsend等人(1989)描述了类似的方法]。对于东京湾淤泥,等于0.001kPa的有效应力对应于12.5的孔隙比。因此,图5(a)所示的理论曲线是使用计算的。理论和实验测量结果在图5(a)中非常一致。此外,用(10)计算的稳态放电速度为,与实测值相比误差为7%。
试验完成时测得的孔隙比分布如图5(b)所示。由于稳态时有效应力分布的不均匀性,局部孔隙比随试件高度变化很大。在试样顶部,由于粘土的高压缩性,孔隙比较大,并随深度迅速减小。在底部,粘土的孔隙比较低,因此压缩性较小,孔隙比几乎是恒定的。稳态下孔隙比分布的理论估算如图5(b)所示,用于比较。为了建立这条曲线,(9)被用来计算垂直有效应力在试件内的分布。然后根据Imai(1979)图13中给出的非线性对压缩性数据)计算相应的孔隙比值。理论和测量之间的一致性在图5(b)中再次令人满意。
图5表明,理论模型适用于水工固结试验分析。除了数学上的简单性,该模型提供了封闭形式的解决方案,可以利用无需数值分析的优势。利用理论模型作为解释的基础,下一节将介绍水力固结试验程序。
试验程序
Imai(1979)、Baxter等人(1995)和Abu Hejleh等人(1996)讨
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[258751],资料为PDF文档或Word文档,PDF文档可免费转换为Word


