表面轮廓数字滤波：第二部分 鲁棒和谷抑制滤波器的应用外文翻译资料

 2022-08-10 15:26:36

英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

表面轮廓数字滤波：第二部分 鲁棒和谷抑制滤波器的应用

帕维尔·多布赞斯基，帕维尔·帕罗斯

关键词：双过程曲面；数字滤波；高斯回归滤波器；鲁棒滤波；谷抑制滤波器

摘要

这是论文“表面轮廓数字滤波”的第二部分。在第一部分中，我们比较了高斯回归滤波器和样条曲线滤波器在不磨合和磨合剖面碎片的情况下的性能。高斯回归滤波器的性能优于样条滤波器。

建立了高斯稳健轮廓滤波技术。采用了几种典型的稳健权函数。谷抑制滤波器也包括在内。分析了对称纵坐标分布的确定性和随机性剖面的滤波结果，并与高斯回归滤波结果进行了比较。在这种情况下，使用高斯滤波器和其他滤波器的波形不均匀性参数应是相似的。计算机生成的轮廓、具有三角形划痕的轮廓和测量的分层表面也应经过过滤。比较了表面形貌畸变和计算时间。

根据比较结果，推荐了一些数字滤波器。

1.介绍

大多数表面都是由一种以上的工艺制造的。由于这两个过程，生成的纹理是纹理的组合。以烧结材料和平台珩磨筒体结构为例。对两种工艺纹理的理解来自于对其独立组件的理解，建议[1,2]对于这种应用，标准剪切偏移量应增加到2.5mm。一个更好的选择是完全不使用过滤器，而是从配置文件本身开始工作。对于负偏斜曲面不适合采用普通高斯滤波。根据标准ISO 13565-1[3,4]，有必要使用双高斯滤波器（Rk）。高斯回归滤波器，工作在不运行的情况下，超出了开发的长度。它的算法基于国际标准的高斯滤波器。然后，建立了高斯稳健轮廓滤波技术。如果畸形值不会导致滤波器平均线（波纹度剖面）失真，则滤波器称为“稳健”。文献[5]列举了一些典型的稳健权函数。文中提出了表面形貌的稳健滤波方法。[6-9]。

其他可能的方法是使用筛选注册表上封套。已经对三维包络面（滚动球面）进行了数值计算[10]。论文[11,12]的作者也使用了3D球。

利用上下包络线可以消除不必要的峰谷。这些滤波器被称为形态滤波器[13-16]。闭合滤波器可用于分层曲面滤波[15]。

研究的基本目的是比较鲁棒滤波器和谷抑制滤波器的性能。

真实的和计算机生成的表面是调查的对象。

完成了以下工作：

bull;分析各种滤波器对正态分布随机剖面的畸变

bull;研究具有三角形划痕的剖面的高通数字滤波引起的误差

bull;研究测量的圆柱体剖面的变化和使用不同滤波器后的高通滤波

bull;推荐最佳滤波器

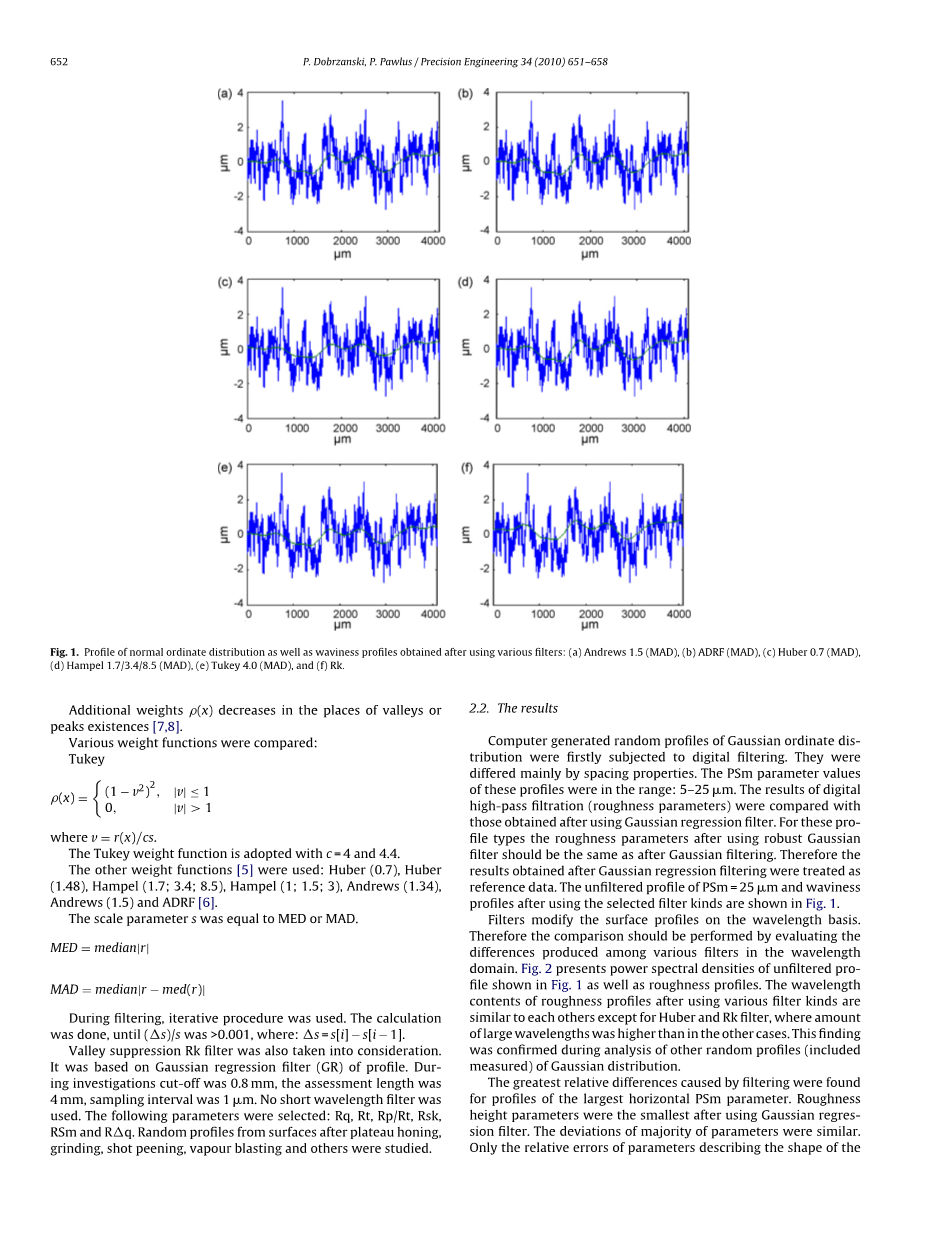
图1。正态纵坐标分布剖面以及使用各种滤波器后获得的波纹度剖面：（a）Andrews 1.5（MAD），（b）ADRF（MAD），（c）Huber 0.7（MAD），（d）Hampel 1.7/3.4/8.5（MAD），（e）Tukey 4.0（MAD）和（f）Rk。

2.剖面滤波分析

2.1条.方法与材料

稳健滤波器是高斯回归滤波器的改进[8]，它使用额外的权重：

附加重量p（x） 谷或峰的位置减少[7,8]。

比较各种权重函数：Tukey

式中v=r（x）/cs。

采用Tukey权重函数，c=4，4.4。

其他权重函数[5]被使用：Huber（0.7）、Huber（1.48）、Hampel（1.7；3.4；8.5）、Hampel（1；1.5；3）、Andrews（1.34）、Andrews（1.5）和ADRF[6]。

标度参数s等于MED或MAD。

MED=中位数| r | MAD=中位数| rminus;MED（r）|

滤波时采用迭代法。计算完成，直到，其中：

谷抑制Rk滤波器也被考虑在内。

它基于轮廓的高斯回归滤波器（GR）。调查期间截止值为0.8mm，评估长度为4mm，采样间隔为1 um、 没有使用短波长滤波器。选择了以下参数：Rq、Rt、Rp/Rt、Rsk、RSm和R⊿q、 研究了平台珩磨、磨削、喷丸、蒸汽喷砂等处理后表面的随机形貌。

2.2.结果

首先对计算机生成的高斯坐标分布随机剖面进行数字滤波。它们的主要区别在于间距特性。这些剖面的PSm参数值在5-25 um、 将数字高通滤波（粗糙度参数）的结果与高斯回归滤波的结果进行了比较。对于这些轮廓类型，使用稳健高斯滤波后的粗糙度参数应与使用高斯滤波后的参数相同。因此，高斯回归滤波后得到的结果作为参考数据。PSm的未过滤轮廓=25um使用所选滤波器类型后的m和波纹度轮廓如图1所示。

滤光片根据波长修改表面轮廓。

因此，应通过评估波长域中不同滤波器之间产生的差异来进行比较。图2示出了图1所示的未滤波轮廓的功率谱密度以及粗糙度轮廓。除Huber和Rk滤波器外，使用不同滤波器后粗糙度分布的波长含量基本相同。这一发现在分析高斯分布的其他随机分布（包括测量的）时得到了证实。

图2。使用各种滤波器后获得的粗糙度轮廓的功率谱密度函数：（a）Andrews 1.5（MAD），（b）ADRF（MAD），（c）Huber 0.7（MAD），（d）Hampel 1.7/3.4/8.5（MAD），（e）Tukey 4.0（MAD），（f）Rk和（g）未滤波轮廓（如图1所示）。

对于最大水平PSm参数的剖面，滤波引起的相对差异最大。使用高斯回归滤波器后，粗糙度高度参数最小。大多数参数的偏差是相似的。只有描述纵坐标分布形状的参数如Rp/Rt（35%）和Rsk（有时大于100%）的相对误差较大。坡度计算误差较小（0.03%）。对于最大波长的剖面，由于滤波不当导致的计算高度和间距参数的最大差异达15%，与稳健滤波器相比，Rk滤波器在描述纵坐标分布形状的参数方面造成了很大的误差。

当使用稳健滤波器时，与MED（Rq至9%，RSm至17%）相比，使用该方法导致参数误差（Rqto6%，RSmto14%）减少。Hampel法（1.7；3.4；8.5）、ADRF和Huber法（1.48）的差异最小。Rq最大差异为1.5%，RSm 5%。使用Tukey（4.4）、Andrews（1.5）、Hampel（1；1.5；3）后的误差较大（Rq高达4%，RSm高达12%）。使用Huber权重（c=0.7）后，误差最大：Rq为6%，RSm为14%，这些误差是应用MAD参数得到的。

图3.使用Rk滤波器和稳健滤波器（Rdq平均R⊿q）.

并对实测的正态纵坐标分布进行了分析。证实了模拟剖面分析中的观测趋势。不同滤光片类型后粗糙度分布的波长含量相似。

对于较大的波纹度，数字滤波引起的误差较大。粗糙度剖面的大畸变发生在最大波长的剖面上。一般来说，尺度参数从MED（Rq的最大误差为20%）到MAD（Rq的最大误差为15%）的变化减少了由稳健滤波引起的大多数参数（RSm参数为豁免）的误差。

使用Hampel（1.7；3.4；8.5），ADRF和Huber（1.48）滤波器后，误差最小。在这些情况下，当使用MAD作为标度参数时，Rq参数的最大变化为2.5%，RSm 6%。应用Tukey（4.4）、Andrews（1.5）和（1.34）滤波器、Rk滤波器、Tukey（4）和Hampel（1；1.5；3）滤波器引起较大的失真（Rq到10%，RSm到14%），我们获得了Huber（0.7）滤波器使用（Rq到15%，RSm到17%）后的最大误差。

通常，在测量和建模剖面分析过程中获得的结果彼此相似。

研究了计算机生成的三角形山谷随机剖面。将粗糙度参数与原始轮廓的粗糙度参数进行了比较。山谷的宽度在50到200之间um、 但是山谷深度在5到20之间um、 不同滤光片使用后的粗糙度分布，当滤光片宽度较小时，其波长含量基本相同。

对于宽波谷，与其他稳健滤波器相比，当使用Huber滤波器时，粗糙度轮廓包含更多的大波长。在这种情况下，使用Rk滤波器后的功率最低（然后Rq参数很小）。图3示出了使用Rk滤波器和鲁棒滤波器后获得的粗糙度参数的最大绝对误差。未过滤的剖面参数为参考数据。数字滤波引起的粗糙度分布畸变最大，谷最宽。滤波的使用通常会导致高度参数Rq、Rt和斜率R⊿q的减小. Rsk减小，RSm减小，空度系数Rp/Rt增大，谷宽增大导致Rp/Rt相对误差增大。斜率估计的偏差最小。使用Rk滤波器通常会造成最大的误差。MAD或MED作为尺度参数，导致粗糙度剖面形状和参数值非常相似。图4.5所示的未滤波剖面和所选的波形线剖面为下图4.5所示的粗糙剖面和未滤波剖面的功率谱密度函数图。表1给出了使用本作者推荐的滤波器和Rk滤波器后获得的未滤波和粗糙度参数。保证与高斯回归滤波结果相似的滤波方法对高斯纵坐标分布的随机剖面进行滤波，导致分析剖面失真较大。因此，选择过滤器类型应该是一个折衷方案。

图4。深谷剖面以及使用各种滤波器后获得的波纹剖面：（a）Andrews 1.5（MAD），（b）ADRF（MAD），（c）Huber 0.7（MAD），（d）Hampel 1.7/3.4/8.5（MAD），（e）Tukey 4.0（MAD）和（f）Rk。

在鲁棒滤波器中，使用ADRF或Hampel函数（1.7；3.4；8.5）后的误差最大，使用安德鲁斯（1.34）、Tukey（4）、安德鲁斯（1.5）、Hampel（1；1.5；3）和Tukey（4.4）权值后的参数变化比未经滤波的剖面小。在使用Huber（0.7）滤波器后，得到了最小的畸变。

影响过滤器选择的另一个因素是迭代步骤的数量。过滤所有具有三角形划痕的分析表面后，其平均值（当MED为标度参数时）为Hampel权重函数（1.7；3.4；8.5）–5.3，ADRF–5.0，Andrews（1.5）–4.4，Huber（1.48）–5.6，Andrews（1.34）–6.4，Huber（0.7）–6.8，Hampel（1；1.5；3）–5.1，Tukey（4）–6.2和Tukey（4.4）–5.2。当MAD是标度参数时，我们收到以下平均迭代步骤数：使用Hampel滤波器（1.7；3.4；8.5）–5.0，ADRF–5.0，Andrews（1.5）–5.2，Huber（1.48）–5.4。

图5.使用各种滤波器后获得的粗糙度轮廓的功率谱密度函数：（a）Andrews 1.5（MAD），（b）ADRF（MAD），（c）Huber 0.7（MAD），（d）Hampel 1.7/3.4/8.5（MAD），（e）Tukey 4.0（MAD），（f）Rk和（g）未滤波轮廓（如图4所示）。

表1使用数字滤波器后含深谷剖面（如图4所示）的未滤波和粗糙度参数值及参数的相对变化

图6。使用Rk滤波器、稳健滤波器，特别是Hampel滤波器（1；1.5；3）后获得的粗糙度参数的最大绝对误差，当MAD是scale参数时（Rdq表示R⊿q）。

图7。平台磨光圆柱体轮廓以及使用各种滤波器后获得的波纹度轮廓：（a）Andrews 1.5（MAD），（b）ADRF（MAD），（c）Huber 0.7（MAD），（d）Hampel 1.7/3.4/8.5（MAD），（e）Tukey 4.0（MAD）和（f）Rk。

图8。使用各种滤波器后获得的粗糙度轮廓的功率谱密度函数：（a）Andrews 1.5（MAD），（b）ADRF（MAD），（c）Huber 0.7（MAD），（d）Hampel 1.7/3.4/8.5（MAD），（e）Tukey 4.0（MAD），（f）Rk和（g）未滤波轮廓（如图7所示）。

Andrews（1.34）–5.7，Huber（0.7）–5.8，Hampel（1；1.5；3）–5.2，Tuke

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[238533]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章