
英语原文共 14 页,剩余内容已隐藏,支付完成后下载完整资料
Fast Exact Search in Hamming Space With Multi-Index Hashing
Mohammad Norouzi, Ali Punjani, David J. Fleet,
{norouzi, alipunjani, fleet}@cs.toronto.edu
摘要
人们越来越关注使用紧凑的二进制串来表示图像数据和特征描述符,以进行快速的近邻搜索。虽然使用二进制串的原因是它们可直接作为哈希表的下标(或地址),但长于32位的代码却没有使用二进制串,这种方式被认为是无效的。我们引入了一种严格的方法来在二进制代码子字符串上构建多个哈希表,从而实现在汉明距离上精确的k最近邻搜索。该方法存储效率高且易于实现。理论分析表明,对于均匀分布的代码,该算法表现出次于线性运行时间的时间复杂度。经验结果表明,对于多达十亿个64位,128位或256位代码的数据集,对比基础的线性扫描,搜索速度有了显著的提高。
- 介绍
人们越来越关注以紧凑的二进制串表示图像数据和特征描述符,通常是为了促进视觉应用中的快速近邻搜索和特征匹配(例如[2],[7],[19],[32],[33],[35])。二进制代码存储效率高,而比较只需少量的机器指令。数百万个二进制代码可以在不到一秒钟的时间内与查询进行比较,但是,对于二进制编码,通常是离散编码,最令人信服的点是它们可用作哈希表的直接索引(地址),与穷举式的线性扫描相比速度呈现出显著的提高(例如,[25],[31],[38])。
然而,直接使用二进制编码作为哈希下标并不一定有效率。为要查找近邻分段,需要在查询中检测某个汉明球内的所有哈希表条目(或存储桶)。问题在于,此类存储桶的数量随搜索半径成指数增长,就算搜索半径变小,需要查询的存储桶通常比数据库中条目的数量更多,因此比线性扫描要慢。关于二进制代码的最新论文提到了哈希表的使用,但是当编码长于32位(例如[20],[25],[31],[35])也诉诸于线性扫描。毫不奇怪,串长度通常都显然长于32位以便于达到令人满意的检索表现。
本文提出一种新的算法达到精确的k-最近邻(kNN)搜索在二进制串上,这种算法显著地比穷举线性扫描快。自从引入在二进制串上使用哈希技术以来,这一直是一个未解决的问题。我们新提出的多索引哈希算法不仅展现出了次线性搜索时间,而且存储效率高,易于实现。根据经验,在不超过1B代码的数据库中,我们发现多索引哈希比线性扫描快数百倍。外推表明,随着数据库大小超过1B代码,加速增益将快速增长。
-
- 背景:问题和相关工作
对二进制串的最近邻(NN)搜索用于图像搜索[29],[35],[38],匹配局部特征[2],[7],[16],[33],图像分类[6],对象分割[19]和参数估计[32]。有时,二进制串直接生成为图像或图像补丁的特征描述符,例如BRIEF或FREAK [2],[6],[7],[36],有时二进制语义是通过从高维数据中离散相似性保持的映射生成的。大多数这样的映射被设计为保留欧几里德距离(例如[11],[20],[29],[33],[38])。其他人则关注语义相似性(例如[21],[25],[26],[30] – [31] [32],[35])。本文我们关注的不是生成代码的算法,而是在汉明距离上的快速搜索。1
1.确实存在着其他有办证的方法来在大的真实值特征图像上进行大致的NN搜索(例如,[3], [17], [27], [24], [5])。然而,在这篇文章中我们将注意力主要放到了紧凑的二进制串的精确搜索上。
我们解决了汉明距离中的两个相关搜索问题。给定一个二进制串的数据库, ,首先是在给定查询中找到中的 k近邻汉明距离串,即kNN搜索汉明距离。Minsky和Papert [23]将汉明空间中的1-NN问题称为最佳匹配问题。他们发现没有比穷举算法明显更快的搜索算法,并好奇是否存在这种方法。
第二个问题就是找出在数据集中,查找所有在指定汉明距离中的串,有时也被称为近似查询问题[13]或等距球中的点位置(PLEB)[15],将查询串表示为g,一个二进制串是给定查询串的r-近邻串,当且仅当该二进制串与g有r或更少位不同。我们将这种r-近邻查询问题定义为:从中找到所有与查询串g为r-近邻的串
解决r-近邻搜索的一种办法是使用填充二进制串的哈希表。并检索索引在查询串 r 位内的所有哈希存储桶(例如 [35])。对于有q位编码的二进制串,需要检索的不同哈希桶的数目为
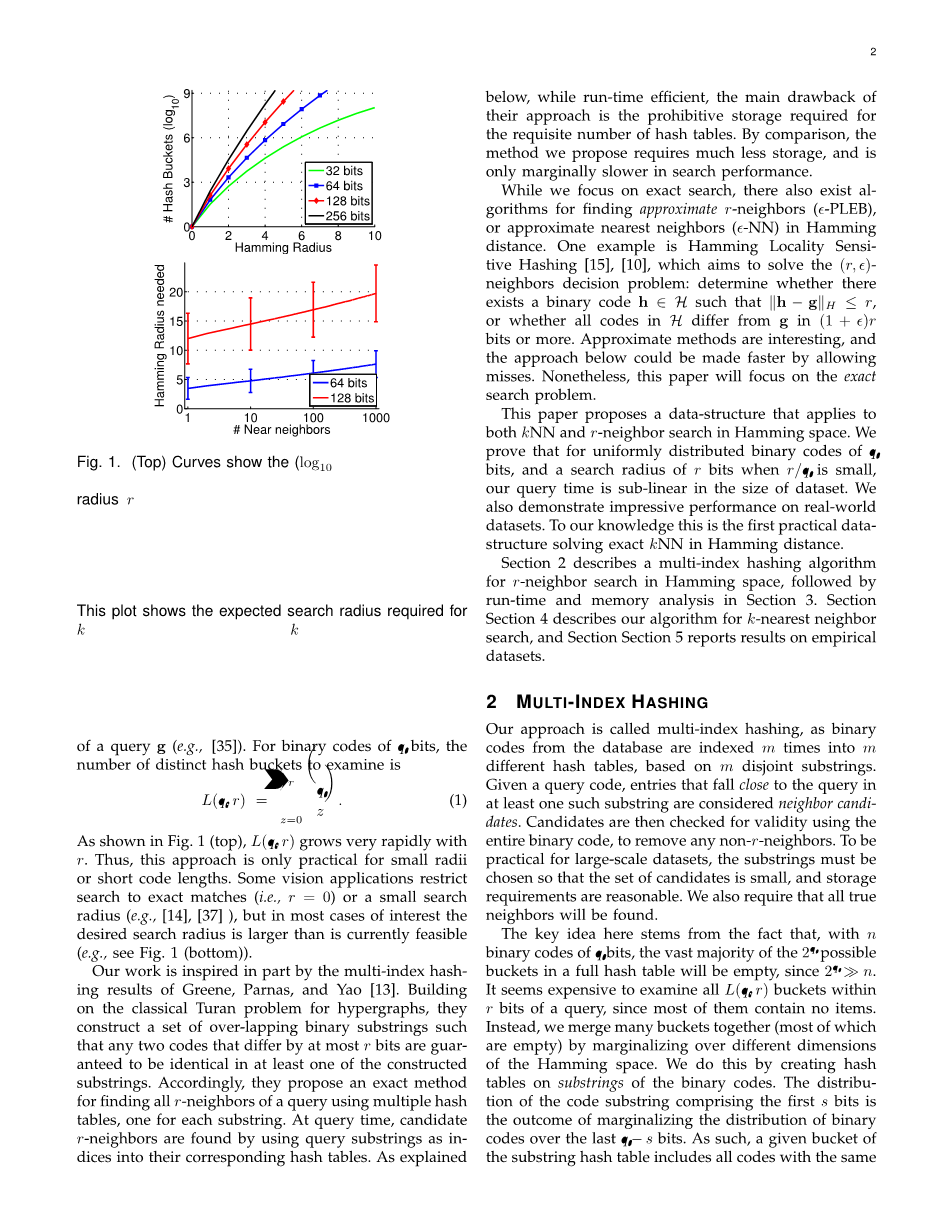
正如图1上部图片(q,r)随着r递增,因此,这种方法之对于小半径搜索或者串长度短有效。有些视觉应用将搜索限定在完全匹配或者小搜索半径之内,但是在大多数情况下感兴趣的搜索半径比当前可行的要大(例如,图一下部图片)。
我们的工作部分受到Greene,Parnas和Yao [13]的多索引哈希结果的启发。他们以经典的图兰超图问题为基础,构造了一组重叠的二进制子字符串,这样任意两个至多有r位不同的代码至少在某一个构造子串上是保证相同的。因此,他们提出了一种精确的方法来寻找所有查询字串的r-近邻串,通过使用多个哈希表,每个表对应一个字串。查询时,通过使用查询子字符串作为它们对应的哈希表的索引来找到候选r-近邻串。如下所述,尽管运行时高效,但是它们方法的主要缺点是难以承受必需数量的哈希表的存储需要。相比之下,我们提出的方法需要更少的存储空间,并且搜索性能仅稍慢一些。
当我们聚焦于精确查询时,也存在在汉明距离上查找粗略r-近邻(),或者大致最近邻()的方法。一个例子是汉明局部敏感哈希[15], [10], 它旨在解决-近邻决策问题:决定是否存在二进制串且,或者在中所有串与g有或更多位不同。粗略的方法很有趣,而且下面的方法在允许失误的情况下可以变得更快。尽管如此,本文还是聚焦于精确查询问题。
图一.顶部曲线显示了在不同串长度下的半径为r的汉明球之内的不同哈希表索引(桶)的数量。使用64位编码,半径为7位的汉明球中大约有1B个存储桶。因此,如果数据库项目少于1B,并且搜索半径为7或更大,则哈希表的效率将低于线性扫描。禁止使用128位编码的哈希表进行半径大于6的搜索(底部)此图显示了k-NN搜索中以k为函数,期望的搜索半径值,在基于1B SIFT描述符的数据集。通过SIFT描述符的随机投影(LSH)获得了64位和128位的二进制串[18]。标准偏差条有助于表明经常需要较大的搜索半径。
本文提出一种能同时应用于汉明空间上k-NN和r-近邻的数据结构。我们证明了对于q位均匀分布的二进制串,同时在r/q很小的搜索半径r上,我们的查询时间在数据集大小上是次线性的。我们还展示了在实际数据集上的出色性能。据我们所知,这是第一个实际的应用在kNN汉明距离上精确解决数据结构的方法。
第二部分介绍了一种用于在汉明空间中进行r-近邻搜索的算法,然后在第三节中进行运行时和内存分析。第四节介绍了我们的ķ-最近邻搜索算法,第五节报告经验数据集上的结果。
- 多索引哈希
我们的方法叫做多索引哈希,数据库中的二进制串基于m个不同的分段被索引m次到m个不同的哈希表中。给定一个查询串,在至少有一个这样的子字符串中接近查询的条目被视为近邻候选。然后,使用整个二进制代码检查候选串的有效性,以删除所有非r-近邻串。为了适用于大规模数据集,必须选择子字符串,以使候选集很小,并且存储要求合理。我们还要求找到所有真正的近邻串被找到。
这里的关键思想源于以下事实:对于n个q位的二进制串,个存储桶中可能有大多数都为空,因为。似乎在一个查询中检测所有的r位存储桶代价太高,因为它们大多数不包含任何项目。相反,我们通过将汉明空间的不同维度边缘化来将许多存储桶合并在一起(其中大多数是空的)。
为此,我们在二进制代码的子字符串上创建哈希表。包含第一个s位子字符串的分布是边缘化最后的q-s位二进制串分布的结果。如此,一个给定字串哈希表的存储桶包含所有相同的前s位,也有剩下的q-s位的中的任意值。不幸地是这些大的存储桶并不限定于给定查询的汉明距离。因此不是所有在聚集桶的条目都是查询串的r-近邻,所以我们需要们剔除所有不是真的r-近邻串。
2.1 子串搜索半径
更细致来说,每个二进制串h,由q位组成,并被分割为m个字串,,hellip;,,每段的长度为位。为了方便起见,我们假设q可被m整除,并且字串包含连续的位。关键思想在于以下语句:当两个二进制串h和g有r或更少位不同时,它们的m个子串中至少有一个子串至多有位不同。这引出了第一个命题:
命题1:如果,这里表示h和g之间的汉明距离,则
这里。
命题一的直接证据来源是鸽巢原理。也就是说,假定m对字串中的每一对的汉明距离都严格大于,则,。显然,由于,这里,则,这与前提条件相矛盾。
命题1的重要性来源于以下事实,子串只有位,在每个子串中必需的搜索半径为。举个例子,如果h和g有3或更少位不同,分段,则4个子串中至少有一个与原串相同。如果它们最多有7位不同,则在至少一个子字符串中相差不超过1位。即我们可以通过在4个子字符串的每一个上搜索1位的半径来搜索7位的汉明半径,更通俗来说,不是搜索个哈希桶,只在m个子串的哈希表中检索个哈希桶就足够了,即,总共有
个哈希桶。
虽然可以只用在m个哈希表中检索半径为就可检索完所有的哈希桶,但是我们将证明这并不一定是必须的。通常可以只在m个子串哈希表中检测的半径,仍然可以确保g的所有近邻串都被找到。特别地,有,这里,要找到q位二进制串的r半径内的任何条目,在半径内检索个子串哈希表就很充分了。剩下的个子串只用检索半径的哈希表。为了不失一般性,子串哈希表是无序的,我们首先用的半径检索前个哈希表,然后剩下的哈希表用的半径检索。
命题2:如果,则
使 (3a)
或 使 (3b)
为了证明命题2,我们证实当(3a)为假命题时,(3b)一定为真。如果(3a)为假命题,则一定有alt;m-1,不然a=m-1,这种情况下命题(3a)就和命题一等同了。如果(3a)为假命题,则h和g在它们的前a 1子串就有或更多位不同。因此,前a 1个子串不同的总位数至少为。因为 ,,也说明剩下的m-(a 1)不同的总位数至多为 。这样,使用命题1,剩下每个m-(a 1)个子串的哈希表最大的搜索半径为
因此命题二为真命题。因为在大搜索半径下的哈希桶数量呈指数增长,命题2提出的子串小半径搜索是必要的。
对于命题2的一个特例是当rlt;m时,,a=r。这种情况下,只用在的搜索半径下搜索r 1个子串哈希表,这种情况下就是完全匹配查询,剩下的m-(r 1)个子串哈希表可被省略。显然,如果查询串不能与选定的r 1中的任意一个完全匹配,则数据库中的串至少与查询串相差r 1位。
2.2 用于r-近邻搜索的多索引哈希
在预处理阶段,给定一个二进制串的数据库,给m个子串每个都建立一个哈希表,正如算法1中所阐述的那样。在查询的时候,给定一个查询串g,有个子串,我们检索与汉明距离为或的第j个子串的哈希表。这样我们就获得了从第j个子串哈希表中的一系列候选串,表示为。根据以上的命题,m个集合的并集,,是g可能的r近邻串的父集。算法的最后一步就是计算候选集中的所有串与g的全汉明距离,保留真正为g的r-近邻串。算法2概述查询g的r-近邻的检索过程。
检索的代价取决于查找量(即,检索的存储桶的数量),和最后检测的候选串的数量。毫不奇怪的是这两者之间有着自然的取舍。大查找量的情况下可以减多余候选串的数量。通过合并查找桶的数量来减少查找量,又会获得大量的待检测候选串。在极端情况下当m=q时,子串只有一位,这时整个数据库几乎都时候选串。
建立多索引哈希的想法并不新奇(例见,[13], [15])。然而之前的研究都依赖于子串的完全匹配。放松这一约束条件就可得到更有效的算法,特别是在大存储量需求的条件下。
3 性能分析
我们接下来提出两种基于搜索表现的分析模型来帮助解决两个关键的问题:(1)搜索成本如何取决于子字符串的长度以及子字符串的数量?(2)运行时间复杂度和存储复杂度如何取决于数据库大小,串长度和搜索半径?
为了帮助回答这些问题,我们利用二项式系数之和的一个公知界线[9];即,对于任意和
这里是伯努利分布的在下的概率熵。
接下来,n还是代表q位二进制串数据库的数据量,r为搜索的汉明距离。m代表哈希表的数量,s代表子串的长度s=q/m。因此,最大的子串的搜索半径为。以上,为了模型的简单性,我们假设q可被m整除。
我们首先确定查找次数的上限。首先,在算法2里面的查找次数m受,子串哈希表的数量,在子串长度为s位,半径下的哈希桶的数量的三者乘积的限制。相应地,使用(5),如果检索半径少于串长度的一半。,则总查找次数为
显然,随着我们减少子串的长度,子字符串的数量随之增加,所需要的查询次数也先成倍减少。
为了分析每个存储桶的预期候选数量,我们考虑将n串二进制串均匀分布在汉明空间上,在这种情况下,对于s位的子串,每个子串的哈希表含有个存储桶,每个存储桶期望的条目数是。因此期望的候选集的大小等于查找次数为。
总查询代价为查找次数乘以候选集检测数。这些代价或随串长度q和哈希表实现方式而不同,根据经验来说,我们发现,以合理的近似值,查找和候选测试的成本是相似的(当qlt;256时)。我们对每个查询的总搜索成本进行建模,为了检索到所有的r-近邻串,以单次查找所需的时间为单位,为lt;
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[237352],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


