
英语原文共 12 页,剩余内容已隐藏,支付完成后下载完整资料
投资组合选择
摘要:投资组合选择的目标是建立投资组合,使预期收益与个人可接受的风险水平最大化。投资组合选择利用历史数据和投资者对未来收益的预期,使用建模技术来量化“预期投资组合收益”和“可接受的投资组合风险水平”,并提供选择最佳投资组合的方法。现代投资组合理论已经给投资管理领域带来了革命性的变化,这么说并不过分。允许管理人员量化投资组合的投资风险和预期收益,为主观的投资管理艺术提供了科学和客观的补充。更重要的是,投资组合管理的焦点曾经是单个资产的风险,投资组合选择理论已经将焦点转移到整个投资组合的风险上。这一理论表明,将风险资产组合起来,产生一个预期收益反映其组成部分的投资组合是可能的,但风险要低得多。换句话说,可以构建一个风险小于其所有单个部分之和的投资组合。
关键词:投资组合选择,现代投资组合理论,均值-方差分析,效用函数,有效投资组合,最优投资组合,协方差,相关性,投资组合多样化,贝塔,投资组合方差,可行资产组合集
在本章中,我们将介绍Markowitz(1952)提出的投资组合选择理论。这个理论也被称为均值-方差投资组合分析或简单的均值-方差分析。
一些基本概念
投资组合理论借鉴了两个领域的概念:金融经济理论和概率统计理论。这一部分介绍了投资组合理论中使用的金融经济理论的概念。虽然这里提出的许多概念有一个更加技术性或严格的定义,其目的是保持简单和直观的解释,以便读者能够欣赏这些概念的重要性和贡献,发展现代投资组合理论。
效用函数与无差异曲线
在生活中有许多情况下,实体(即个人和公司)面临两个或更多的选择。经济名词“选择理论”使用冯bull;诺依曼和摩根斯特恩(1944)提出的效用函数概念来描述实体在面对一系列选择时作出决定的方式。效用函数为实体所面临的所有可能选择分配一个(数值)值。一个特定选择的价值越高,那个选择带来的效用就越大。所选择的选项是在给定实体面临的一组(预算)约束条件下产生最大效用的选项。
在投资组合理论中,实体也面临着一系列的选择。不同的投资组合具有不同的预期收益和风险水平。此外,预期回报率越高,风险就越大。实体面临着从所有可能的风险/收益组合中选择一个投资组合的决定:其中收益是可去除的,增加了效用水平,而风险是不可取的,降低了效用水平。因此,实体从不同的风险/收益组合中获得不同程度的效用。任何可能的风险/收益组合所获得的效用用效用函数来表示。简单地说,效用函数表达了实体对感知风险和预期收益组合的偏好。
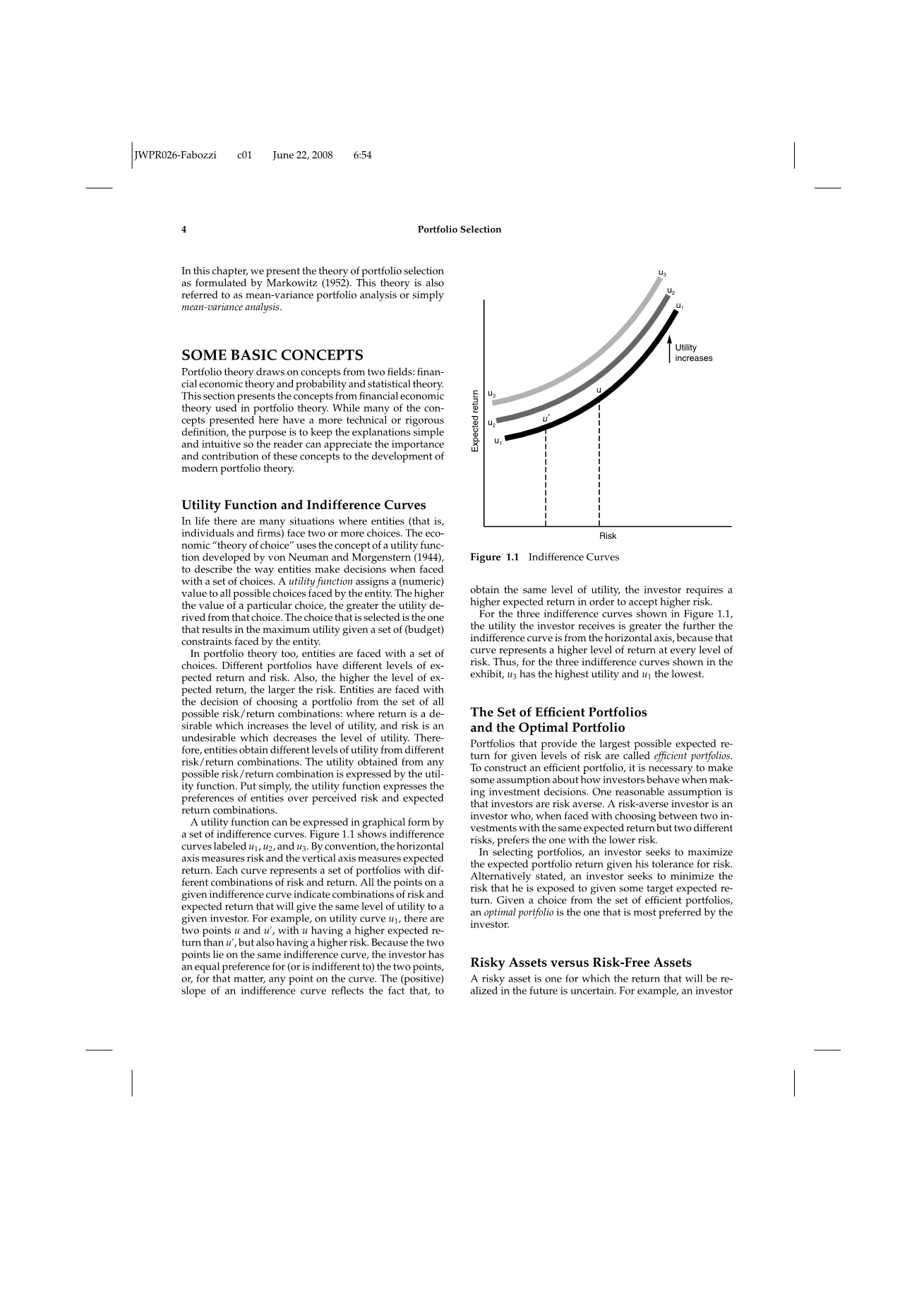
效用函数可以用一组无差异曲线以图形的形式表示。图1.1显示了标记为u1、u2和u3的无差异曲线。按照惯例,横轴衡量风险,纵轴衡量预期收益。每条曲线代表一组不同风险和收益组合的投资组合。一个给定无差异曲线的所有点表示风险和预期回报的组合,将给予给定的投资者相同的效用水平。例如,在效用曲线u1上,有两个点u和u,其中u的预期回转率高于u,但风险也较高。因为这两点位于同一无差异曲线,所以投资者对这两点,或者说曲线上的任何一点都有相同的偏好。无差异曲线的(正)斜率反映了这样一个事实: 当投资者获得相同的效用水平时,为了接受更高的风险,他们需要更高的预期收益。
对于图1.1所示的3条无差异曲线,投资者收到的效用越大,无差异曲线距离水平轴越远,因为这条曲线代表了每一个风险水平的更高收益水平。因此,在展示的三个无差异曲线中,u3的效用最高,而u1的效用最低。
图1.1无差异曲线
有效投资组合的集合和最优投资组合
为给定风险水平提供最大可能预期回报的投资组合称为有效投资组合。为了构造一个有效的投资组合,有必要对投资者在进行投资决策时的行为做出一些假设。一个合理的假设是,投资者是风险厌恶者。风险厌恶型投资者是指当面临两种具有相同预期回报但不同风险的投资时,偏好风险较低的投资者。
在选择投资组合时,投资者寻求最大化的预期投资组合收益,给予他的风险承受能力。换句话说,一个投资者寻求最小化风险,他所面临的风险,给予一些目标预期回报。如果从一组有效的投资组合中进行选择,最优投资组合是投资者最喜欢的投资组合。
风险资产与无风险资产的比较
风险资产是指未来重新投资的回报率不确定的资产。例如,一个投资者购买了辉瑞公司的股票,打算持有一段时间,但他们不知道在持有期结束时会得到什么回报。回报将取决于辉瑞公司股票在出售时的价格以及公司在持股期间支付的股息。因此,辉瑞的股票,实际上是所有公司的股票,是一种风险资产。
美国政府发行的证券也是有风险的。例如,投资者购买30年到期的美国政府债券,如果这种债券只持有一年,他不知道会实现多少回报。这是因为当年的利率变动会影响一年后债券的价格,并且会影响当年债券的回报。
然而,有些资产的回报在今天是确定无疑的。这类资产被称为无风险或无风险资产。无风险资产通常被定义为美国政府的短期债务。例如,如果一个投资者购买了一年到期的美国政府债券,并计划持有该债券一年,那么该债券的回报率就不存在不确定性。(注:此处的「报税表」是指名义报税表。经通胀调整后的“实际”回报率尚不确定。)投资者知道,在一年内,证券的到期日,政府将支付一定数额的债务清偿。注意这种情况对于30年后成熟的美国政府安全是多么的不同。虽然1年期和30年期证券是美国政府的债务,但前者在一年内到期,因此不存在实现回报的不确定性。相比之下,尽管投资者知道政府在30年后将为30年期债券支付多少,但他不知道一年后债券的价格将是多少。
衡量投资组合的预期收益
我们现在准备定义实际和预期回报的风险资产和投资组合的风险资产。
计算单期投资组合收益
一个资产组合在某个特定时期的实际回报率可以用以下方法直接计算出来:
|
Rp = w1 R1 w2 R2 . . . wG RG |
(1.1) |
Rp:本期投资组合收益率
Rg:本期g资产收益率
Wg:资产g在投资组合中的权重(即资产g的市场价值占总投资组合市场价值的比例)
G:投资组合中的资产数量
方程式(1.1)用简写表示如下:
Rp
等式(1.2)指出,g资产的投资组合(Rp)的收益等于投资组合中所有个别资产权重的总和乘以各自的收益。投资组合收益Rp有时被称为持有期收益或事后收益。
例如,考虑以下由三种资产组成的投资组合:
|
资产 |
持有期初市值 |
持有期收益率 |
|
1 |
6百万 |
12% |
|
2 |
8百万 |
10% |
|
3 |
11百万 |
5% |
该组合在持有期开始时的总市值为2,500万元。注意,权重之和等于1。通过引入方程(1.1),我们得到了持有期的投资组合收益率,
Rp =0.24(12%) 0.32(10%) 0.44(5%)=8.28%
请注意,由于持有期的投资组合回报率为8.28%,在持有期内投资组合价值的增长额为(2500万美元)0.0828207万美元。
风险资产组合的预期收益
等式(1.1)显示了如何计算一个投资组合在特定时间段内的实际收益。在投资组合管理中,投资者也希望知道风险资产组合的预期(或预期)回报。投资组合的预期收益率是投资组合中每项资产预期收益的加权平均数。分配给每项资产预期收益的权重是该资产的市场价值占投资组合总市场价值的百分比。就是,
E (Rp) =w1 e (R1) w2 e (R2) ... wG e (RG) (1.3)
E()表示期望值,而e(RP)有时被称为事前收益,或者在某个特定时间段内的预期投资组合收益。
风险资产i的预期收益率e(Ri)计算如下。首先,必须指明可能实现的回报率的概率分布。概率分布是一个函数,它为一个随机变量的所有可能结果赋予一个概率。考虑到概率分布,预期的随机变量的值就是可能结果的加权平均值,其中加权是与可能结果相关的概率。
表1.1股票收益率的概率分布
|
n |
收益率 |
发生概率 |
|
1 |
12% |
0.18 |
|
2 |
10 |
0.24 |
|
3 |
8 |
0.29 |
|
4 |
4 |
0.16 |
|
5 |
-4 |
0.13 |
|
合计 |
1.00 |
在我们的例子中,随机变量是不确定的资产收益率i。在为可能的收益率指定了一个概率分布之后,资产收益率i的预期值就是所有结果的加权平均数。最后,我们不使用“资产回报的预期价值”这个术语,而是使用“预期回报”这个术语数学上,资产i的预期收益表示为:
E(Ri ) = p1 R1 p2 R2 bull; bull; bull; pN RN (1.4)
Rn:资产i的可能回报率为n
Pn:资产i的收益率为n的概率
N:回报率的可能结果数
我们如何规定一项资产的回报概率分布?我们将在本章后面看到,在大多数情况下,回报的概率分布是基于历史回报的。基于不确定性投资行为的过去表现对不同收益结果的概率分配是对概率分布的一个很好的估计。然而,为了举例说明,假设一个投资者正在考虑一个投资,股票XYZ,它有一个概率分布的回报率在一段时间内,如表1.1给出。股票有5种可能的回报率,概率分布指定了每种可能结果的发生概率。
用方程(1.4)代换得到:
E (Rxyz) = 0.18(12%) 0.24(10%) 0.29(8%) 0.16(4%) 0.13(- 4%) = 7%
因此,7%是股票收益率XYZ的预期收益率或概率分布的平均值。
衡量投资组合风险
字典对风险的定义是“风险、危险、损失或伤害风险” 用各种定义来描述风险。Markowitz(1952,1959)使用众所周知的方差和协方差的统计措施量化了风险的概念。他将投资组合的风险定义为投资差异和投资之间协方差的总和。在投资组合中引入投资回报之间的协方差来衡量投资组合的风险这一概念永远地改变了投资界对风险概念的看法。
方差和标准差作为衡量风险的标准
随机变量的方差是对可能结果围绕期望值(平均值)的离散度或可变性的度量。在资产收益的情况下,方差是可能收益率与预期收益率之间的离散度。
资产i的预期收益的方差表示为var(Ri)
Var (Ri) = p1[ r1-e (Ri)]2 p2[ r2-e (Ri)]2 hellip;hellip; pN [ rN-e (Ri)]2
或者 Var (Ri)
使用股票收益率的概率分布我们可以举例说明方差的计算:
Var (Rxyz) = 0.18(12%-7%)2 0.24(10%-7%) 0.29(8%-7%)2 0.16(4%-7%)2 0.13(- 4%-7%)2
=24.1%
与收益分布相关的方差度量了收益分布集中在均值或预期收益率周围的紧凑程度。马科维茨认为,这种紧凑性或方差等同于投资的不确定性或风险。如果一项资产是无风险的,那么它的预期收益分散度为零。换句话说,回报(在这种情况下也是预期回报)是确定的,或者是有保证的。
标准差
由于方差是平方单位,通常可以看到方差以方差的正平方根转换成标准差:
SD(Ri)=
对于股票XYZ来说,标准差是
SD(Rxyz) = = 4.9%
方差和标准差在概念上是等价的,也就是说,方差或标准差越大,投资风险越大。
对于使用方差作为风险的度量标准,有两种批评。第一个批评是,由于方差衡量
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[236507],资料为PDF文档或Word文档,PDF文档可免费转换为Word


