
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
钢筋混凝土填充墙钢框架组合压杆的有效简化模型
概要:为解决钢筋混凝土(RC)填充墙的部分约束的钢框架的滞回性能的微观数值分析预测不准确的问题,在对PR钢框架填充墙裂缝分布、荷载传递机理和破坏模式进行试验观测的基础上,提出了一种新型的复合压杆简化模型。本文提出的实心RC填充墙组合压杆模型由alpha;斜压杆和主斜压杆组成。alpha;斜撑用于反映剪力连接件沿框架-墙界面抵抗的部分侧向力,由于钢框架与钢筋混凝土填充墙之间的相互作用比较复杂,所以为了考虑沿对角线方向传递的剩余侧向力,引入了主斜撑。本文分别推导了alpha;斜撑和主斜撑有效宽度的计算公式。以钢筋混凝土填充墙PR钢框架为例,采用复合斜压杆模型进行了数值模拟。由该模型得到的最大抗侧力和滞回曲线形状与试验结果吻合较好,当层间位移小于1%时,可以较准确地预测钢筋混凝土填充墙PR钢框架的骨架曲线。当层间位移比大于0.5%时,该简化模型也能较好地预测结构刚度和等效粘滞阻尼比。
关键词:PR连接;钢框架;填充墙;剪力连接件;滞回性能;支撑
- 介绍:
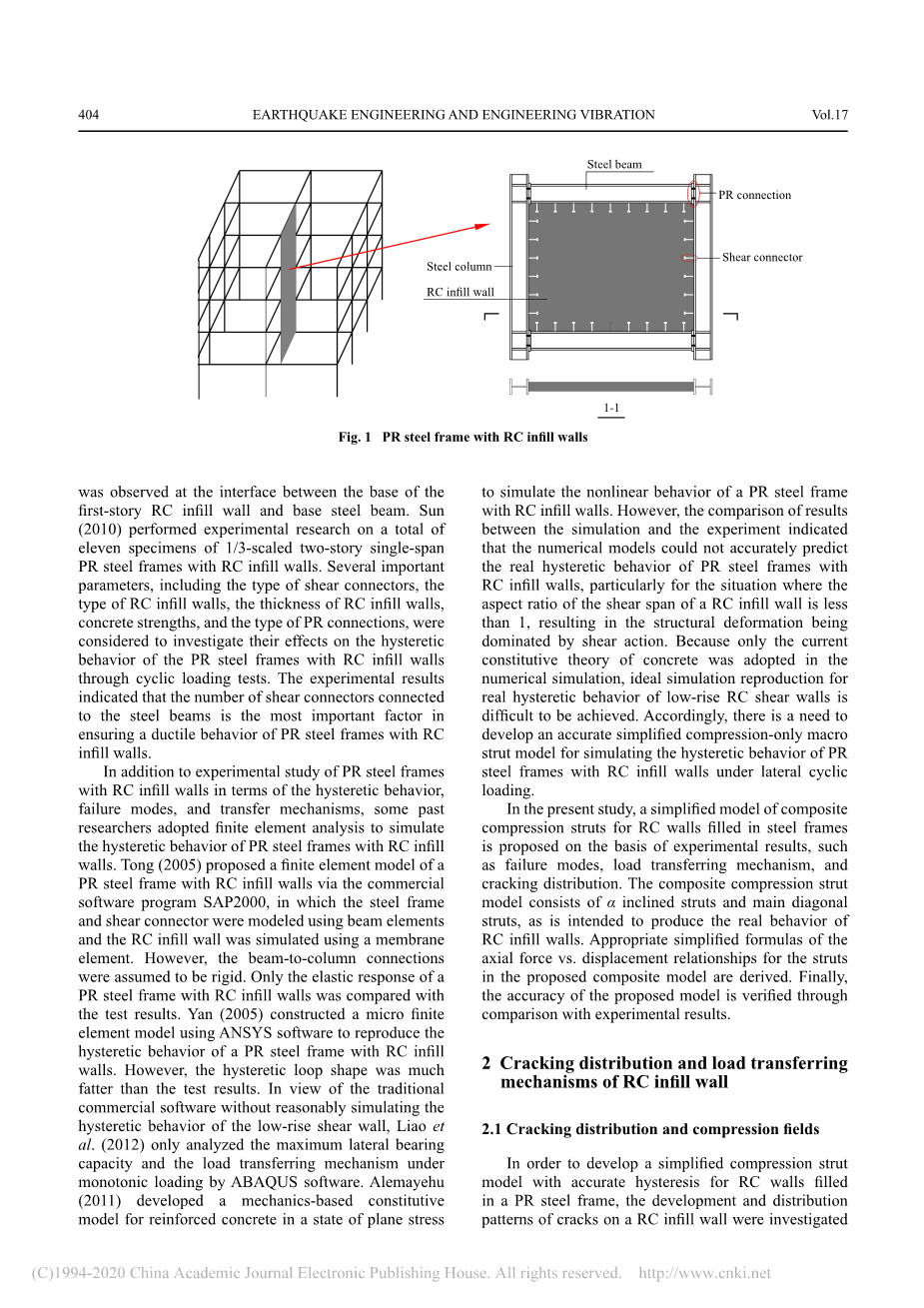
- 带有实心钢筋混凝土(RC)填充墙的部分约束(PR)钢框架是一种创新的复合结构体系,由PR钢框架、钢筋混凝土填充墙以及PR钢框架和钢筋混凝土填充墙之间接口处的剪力连接件(Hajjar,2002;见图1)组成。这种设计细节合理的组合结构具有显著的高侧向强度和刚度、大延性和超耗能能力,可作为地震区有效的抗侧力体系(Sun等人,2010)。近年来的相关研究主要集中在组合结构体系的抗震性能的试验研究上(Tong,2001;Liao等人,2009;Peng和Gu,2013年;Hou等人,2016)。Tong et al.(2005)进行了准静态循环试验,研究了1/3比例的两层单跨PR钢框架与RC填充墙的滞回性能。试验结果表明,采用双腹板角钢结构的梁-柱节点,显著提高了节点的转动能力,避免了传统刚性节点的脆性断裂。然而,钢筋混凝土填充墙PR钢框架的峰值后强度迅速下降成为另一个重要问题。Peng和Gu(2013)还使用准静态加载试验研究了带有RC填充墙的两层单跨PR钢框架。所观察到的实验现象验证了在RC填充墙中存在多传递横向荷载路径的发现。然而,连接在钢梁上的剪切接头在循环荷载作用下发生断裂破坏,导致试件的延性较低。为了提高结构延性并克服这些缺陷,一些研究尝试使用不同类型的连接和剪切连接器(Yan,2006;Sun,2010)。Yan(2006)实验研究了一个两层的单跨全约束钢筋混凝土填充墙钢结构。然而,在一层钢筋混凝土填充墙基础与基础钢梁之间的界面处出现了意想不到的剪切破坏。Sun(2010)对11个1/3比例的两层单跨PR钢框架加RC填充墙试件进行了试验研究。几个重要的参数,包括剪切连接器的类型,钢筋混凝土填实墙的类型,钢筋混凝土填实墙的厚度,混凝土的优势,和公关关系的类型,被认为是研究其对公关的滞回行为的影响钢结构与钢筋混凝土填实墙通过循环荷载试验。试验结果表明,连接钢梁的剪力连接件数量是保证钢筋混凝土填充墙PR钢框架延性的最重要因素。
PR钢框架加RC填充墙的滞回性能、破坏模式、传递机理等方面的试验研究,过去的一些研究人员采用有限元分析的方法来模拟PR钢框架加RC填充墙的滞回性能。Tong(2005)通过商业软件SAP2000提出了钢筋混凝土填充墙PR钢框架的有限元模型,其中钢框架和剪力连接器采用梁单元建模,钢筋混凝土填充墙采用mmbrane单元模拟。然而,梁柱之间的连接被认为是刚性的。本文仅对钢筋混凝土填充墙PR钢框架的弹性响应与试验结果进行了比较。Yan(2005)利用ANSYS软件建立了微型有限元模型,再现了钢筋混凝土填充墙PR钢框架的滞回性能。然而,滞回曲线形状比试验结果要大得多。Liao等(2012)针对传统商业软件没有合理模拟低层剪力墙的滞回行为,仅利用ABAQUS软件分析了单调荷载作用下的最大侧向承载力和荷载传递机制。Alemayehu(2011)提出了一种基于力学的钢筋混凝土平面应力状态下的本构模型,用以模拟具有钢筋混凝土填充墙的PR钢框架的非线性行为。然而,仿真与实验结果的比较表明,数值模型无法准确预测真正的公关钢框架的滞回行为与钢筋混凝土填实墙,尤其是对长宽比的情况下的剪跨钢筋混凝土填实墙小于1,导致结构变形是由剪切动作。由于数值模拟中只采用了现行的混凝土本构理论,难以实现对低层剪力墙真实滞回行为的理想模拟再现。因此,有必要建立一个精确的、简化的、只考虑压缩的宏观支撑模型来模拟PR钢框架在横向循环荷载作用下的滞回性能。
本文根据试验结果,从破坏模式、荷载传递机理、裂缝分布等方面,提出了钢筋混凝土框架内墙复合压杆的简化模型。复合压缩支撑
模型由alpha;斜支撑和主对角线支撑组成,旨在产生真正的行为的钢筋混凝土填实墙。推导了复合模型中杆件轴力与位移关系的简化公式。最后,通过与实验结果的对比,验证了模型的准确性。
2填充墙的裂缝分布和荷载传递机制
2.1 裂缝分布和受压区域
为了建立具有精确迟滞的简化后的钢筋混凝土填充墙压缩应力模型,研究了钢筋混凝土填充墙裂缝的发展和分布规律如图2所示(Sun,2010)
如图2所示,由从周围的钢架的克制行为,钢筋混凝土填实墙开发了一系列密集斜裂缝与水平方向约plusmn;45ordm;角、横向剪切力引起的。混凝土加密墙在反向循环负载下表现出网格分布,证明了钢筋混凝土填实壁横向载荷转移通过这些大约45ordm;倾斜压缩struts或alpha;倾斜压缩struts(图2 (a))。随着侧向荷载的增大,连接钢梁与钢筋混凝土填充墙的剪力连接件逐渐变形,在界面处出现轻微的滑移,导致钢柱与钢筋混凝土填充墙之间的相互作用更加复杂。因此,钢筋混凝土填充墙墙角的大部分混凝土被压碎。部分侧向荷载沿主对角方向传递,形成主对角压杆(见图2(b))。
图3为钢筋混凝土填充墙的横向荷载传递机理。如图3所示,RC填充墙中墙角混凝土附近的破坏进一步验证了这种荷载传递路径。因此,钢筋混凝土填充墙可以模拟成一系列简化的双向压缩只倾斜杆。
2.2横向荷载转换机制
基于RC填充墙PR钢框架的试验结果(Tong et al,2005;(Sun et al.,2011),侧向荷载通过三种理想化的机制传递到结构基础上:
(1)剪力连接件与RC填充墙相互作用(Vstud,图3)
(2) PR钢框架与RC填充墙相互作用产生的主对角撑(Nstuct,见图)。3
(3)个别PR钢框架的行为
3 部分约束钢筋混凝土填充墙钢框架组合斜压杆简化模型
在本节中,基于观测到的荷载,提出了PR钢框架填充墙复合斜压杆简化模型上述压缩区域中的传输机制。图4说明了使用复合斜压杆的简化模型的组成。简化模型由两种斜压杆(图4(a)):alpha;斜杆(图4(b))和主斜杆(图4(c))组成。为了建立这种简化的分析模型,最重要的一步是确定alpha;斜撑的最小数目。Sun(2010)建议至少使用7个支柱来模拟和反映RC填充墙的整体力学行为。钢筋混凝土填充墙PR钢框架试验研究发现裂缝的倾斜角度大约等于45度。因此,为简单起见,在当前简化模型中,alpha;的值取45度。此外,还提出了主斜撑来传递钢筋混凝土填充墙沿斜向的轴压。钢筋混凝土填充墙转角处的压碎进一步验证了这种类型的加载路径根据Tong等人的实验结果。(2005年)。值得注意的是,周围PR钢框架对RC填充墙的约束作用显著提高了钢框架填充墙的侧向强度,改善了其变形能力,提高了其耗能能力。因此,有必要将主斜撑与alpha;斜撑结合起来。
采用以下假设确定复合斜压杆模型的几何和机械性能:
(1) 钢筋混凝土填充墙与钢梁的界面滑移忽略不计,
(2) 不考虑钢筋混凝土填充墙与钢柱之间的间距,
(3) alpha;斜撑只承受压缩力,忽略了抗拉能力,
(4) 根据混凝土的应力应变关系,推导了主斜撑的恢复模型,
(5) 所有这些支柱都与钢框架连接在一个固定的边界条件下。
3.1复合材料斜压杆模型的几何结构
3.1.1 PR钢框架模型的几何结构
PR钢框架模型的几何结构图5显示了PR钢框架的典型布置,其中和分别是钢柱和钢梁的深度。在简化的组合斜压杆模型中,可以通过位于钢构件中心轴上的梁单元来模拟钢柱和钢梁。PR连接在一定程度上降低了钢框架的侧向强度和刚度。但节点的转动变形能力明显增强。同时,避免了钢架连接处的断裂失效。表示PR连接的机械性能的旋转弹簧放置在柱中心轴的/2处。
3.1.2钢筋混凝土填充墙几何模型
复合斜压杆模型由alpha;斜压杆和主斜压杆组成。由于主斜撑的确定比alpha;斜撑的确定简单,因此本文提供的描述仅集中于alpha;斜撑。图6描绘了钢筋混凝土填充墙中alpha;斜撑的几何结构,其中h是从钢梁中心到中心测量的层高,l是从钢柱中心到中心测量的跨度,alpha;是支柱和钢梁之间的斜角(研究中使用45°),是alpha;斜支柱的宽度。根据钢筋混凝土填充墙的几何关系,alpha;斜撑的宽度可计算为
其中是alpha;斜支柱的数量。
3.2机械性能
3.2.1钢框架
采用具有双线性应力应变关系的纤维截面单元模拟钢框架结构。利用双线性运动硬化塑性模型,考虑了钢在循环载荷作用下的Bauschinger效应。图7显示了钢的循环应力应变关系。
3.2.2 PR连接
钢筋混凝土填充墙预应力钢框架采用顶底角钢和双腹板角钢的预应力连接。因为钢框架与钢筋混凝土填充墙之间复杂的相互作用时,主斜撑产生一定的抗侧力,导致钢梁产生轴向拉力。由于PR连接件的抗弯承载力降低,张力也由PR连接件承受。考虑循环滞回效应的简化连接模型详细推导了拉伸力的影响。图8显示了PR连接的三线性循环力矩与旋转的关系
考虑轴向力效应的PR连接的用户定义的三线性循环力矩-旋转公式如下:
其中M为连接力矩,为连接的初始刚度,theta;为连接转动,theta;y为屈服转动,为最大力矩开始时的转动,和分别为考虑拉力效应的PR连接的屈服力矩和极限力矩。
分别考虑张力效应。钢筋混凝土填充墙PR钢框架PR节点的弯矩-拉力相互作用方程(Tong,2001)用于计算
式中,是PR连接件所承受的拉力,其计算为连接到PR连接件的钢柱腹板的屈服剪力;和分别是PR连接件的屈服力矩和屈服抗拉强度。此外,PR连接件的屈服力矩()分别由三个屈服力矩、和从顶角、座角和双腹板角贡献,如等式(4)所示。类似地,PR连接件的屈服抗拉强度()由顶角屈服抗拉强度()、座角屈服抗拉强度()和双腹板角屈服抗拉强度()贡献,如等式(5)所示。
考虑拉力效应的PR连接的极限力矩也由式(3)确定,式中用钢的极限抗拉强度代替钢的屈服抗拉强度来计算,和。
顶部和阀座角以及双腹板角连接件的初始转动刚度(Kishi等人,1990)取为
式中,E是杨氏钢模,和分别是顶角和腹板角的惯性矩;、和分别是顶角和腹板角的厚度;是顶角支腿中心和座角中心之间的距离,为顶角支腿中心距螺母固定支座的距离,为顶角支腿中心距螺母固定支座的距离,阀座角的旋转中心和腹板角产生的拉力中心,是腹板角支腿中心和连接到腹板角的螺母固定支架之间的距离。
3.2.3 alpha;斜撑
根据混凝土的应力应变关系,推导了alpha;斜压杆的轴力位移滞回系数。为简便起见,假定混凝土的峰后应力保持为最大压应力。然后,混凝土的应力应变关系(Hognestad等人,1955)表示为
式中,是混凝土的最大抗压强度,而是对应于峰值抗压强度的混凝土应变(可以取0.002)。钢筋混凝土填充墙开裂后,压缩场作用沿alpha;倾斜方向发展。然而,在框架-墙界面处发生滑移,使得alpha;斜撑在某些情况下很难被压碎。这种现象意味着整个RC填充墙不起传递全侧向剪力的作用。alpha;斜压杆的抗侧剪性能取决于钢筋混凝土的抗剪性能与钢梁连接的填充墙和剪力连接件。当沿梁-墙界面采用过多的抗剪连接件时,钢筋混凝土填充墙在屈服前达到极限抗剪强度
连接件的抗剪承载力取alpha;斜压杆的抗剪承载力的抗剪承载力。反之,如果与钢梁连接的抗剪连接件数量不足,则抗剪连接件将在钢筋混凝土填充墙破坏之前屈服。因此,alpha;斜压杆的抗剪承载力等于连接到钢梁的剪力连接件的抗剪承载力。因此,alpha;斜撑的抗剪承载力可以确定为
当钢筋混凝土填充墙中采用有头螺栓作为剪力连接件时,Vstud(Saari等人,2004;AISC,2016)可计算为:
式中,Psi;是考虑低周疲劳对有头螺栓影响的折减系数,ns是与钢梁连接的有头螺栓数量,是混凝土的弹性模量,因为,b是有头螺柱的横截面积,gamma;是有头螺柱的极限强度与屈服强度之比,是钢的屈服强度。如果钢筋混凝土填充墙PR钢框架中采用槽钢作为抗剪连接件,则(AISC,2016)可计算为:
式中是通道法兰的厚度,是通道腹板的厚度,是通道抗剪连接件的长度。当斜压杆的抗剪承载力受RC填充墙破坏控制时,定义
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[235356],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


