英语原文共 12 页，剩余内容已隐藏，支付完成后下载完整资料

对在浮动负载情况下的电厂头座寿命的评估

T.P. Farragher ^a, S. Scully^b, N.P. Orsquo;Dowd^c, S.B. Leen^a,

1. 机械和生物医学工程师，瑞安环境研究所, 海洋和能源研究院，爱尔兰国立高威大学，爱尔兰
2. ESB能源国际，ESB总公司，费茨威廉街27号，都柏林，爱尔兰
3. 机械工程系，航空航天和生物医学工程专业、材料和表面科学研究所，利默里克大学、爱尔兰

文章信息

2012年8月14号收到初稿

2012年12月4号收到修订稿

2012年12月17号通过审核

2012年12月23日发表

关键词:

机械热疲劳 高温粘弹效应 柔性车间操作 Ostegren临界平面 复几何学 子模型 有限元

摘要:

在实际载荷条件下，提出了一种在实际载荷情况下的次临界电站出口热机械疲劳分析的有限元方法。该方法包括（i）瞬态传热模型，（ii）连续变温循环塑性模型和（iii）在Ostergren临界平面的多轴疲劳指标参数。该方法允许在关键的位置的局部热应力应变响应识别以及对疲劳寿命和在复杂的非稳态下开裂方向的预测、非等温、循环弹塑性蠕变材料行为。通过测得的工厂数据，以蒸汽管的温度瞬变和蒸汽压力数据的形式，来确定换热常量和验证预测的热响应，尤其要注意设备启动和调度的影响。预测显示在头内表面和外表面的温度的应变响应不同步。冷却瞬态预测将会产生控制损伤和产生裂纹内孔，而加热瞬态预测显示在焊接位置有更具破坏性的影响。在这一个有代表性的测试周期中捕捉到了显着的热机械循环损伤的实际周期。裂纹产生的方向和位置以及工件寿命的预测结果与工业经验相一致。

2012年爱思唯尔公司版权所有

正文:

1.简介

有必要了解在高温高压下的候选电厂材料的性能。以9–12% Cr钢等材料为例，由于其优良的机械性能，比如钢P91和P92已经被应用在发电厂[ 1 ]。目前有越来越多传统的化石燃料发电厂转向可持续能源的趋势，例如风力发电。为了满足多种可再生自然能源的供应，就必须对现有的工厂，设计一套“基本负荷”的运营模式，通过相对应的罕见的关闭与启动，在负荷响应模式下，以关闭和启动频率的特性增加。这个已经成为高温材料和构件的设计评价的重要问题，加压装置更注重热机械疲劳（TMF）和蠕变疲劳失效。

目前头座的设计不考虑循环热应力和负载循环，可导致蠕变疲劳损伤[ 2 ]。在[ 3 ]中进行的工作已经认识到，重复启动和停止操作会导致发电厂的组件产生蠕变疲劳载荷。在[ 4 ]中，复杂的电厂的P91钢几何形状的热力耦合模型，对弹塑性材料模型施加不同的热和机械负荷以体现了工厂启动的影响（无应变率效应）。在[ 5-7 ] 中对/4Cr–1Mo钢–电站组件的使用寿命进行了研究，基于线弹性有限元分析，预计低估了部件的使用寿命。在[ 8 ]中，强调了建模的全局几何和局部子部分的头座几何形状的头几何形状寿命评估的重要性。

在这项工作中，我们采用了之前发表的方法[ 9 ]的现实了一部分电厂的头座。这种方法采用了温度相关的材料特性，以捕捉在启动过程中的材料的行为的材料行为。现实的加载历史的高温蒸汽加压P91钢管进行了研究，为预测一个存根P91蒸汽联箱的热机械循环行为。有限元（铁）分析是用来确定在头上的危险部位。通过一个线性子模型技术进行网格细化，来寻找这些危险位置的部位和以及实现对寿命的预测。

随后的代表周期的出现，是建立在一个简化的版本的现实周期上。通过对代表周期的分析确定的装置运行周期的显著特征，从而快速而准确的得到对部件寿命的估计。

瞬态传热模型的开发，是为了预测相关的温度分布的管道壁厚，以及之后的热力耦合分析。等温循环，弹性-塑性蠕变分析的本构模型是基于[ 9 ]上提出的，以代表的材料的热机械响应。通过多轴向临界平面（CP）的方法[ 10 ]，实现了对部件的寿命预测。使用Ostergren热机械疲劳参数作为疲劳指标参数（FIP）。目前的工作分析电厂头是在热诱导的低周疲劳（LCF）下加载的，在应力应变最大可能不一致，这是由于非线性应力应变响应造成的。该Ostergre FIP中，它是基于应变能，通过结合最大拉应力与相关平面的非弹性应变范围[ 11 ]，使FIP适用于等温的高温低周疲劳失效。

1. 实现方法

2.1 概述

这项工作的总体目标是开发一个寿命预测方法，对电厂组件进行复杂的热力耦合载荷分析预测。该方法的关键之处在于，在已知的实际载荷下预测的热机械温度应力-应变响应。这就要求建立（I）一个热学模型，可以预测在这样的组件的热梯度，（ii）连续变温循环，为总管材料的粘塑性的基本模型。总管的几何尺寸与在爱尔兰的化石燃料发电站的出口总管对应的尺寸相关。为了有效性，使用了一个通用的子建模技术，但要得出准确的解决方案，困难之处在于这个复杂的三维热力耦合问题。

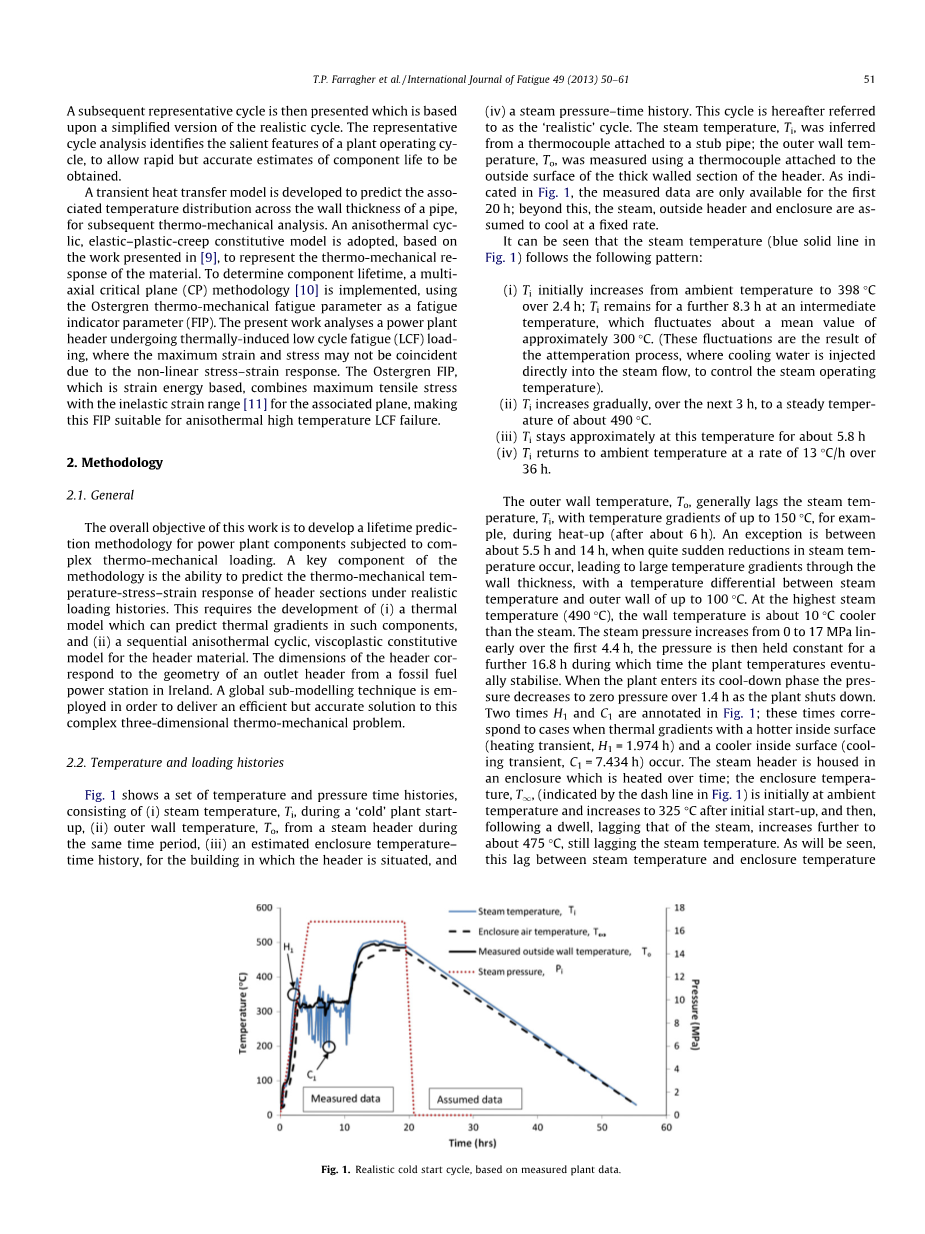
2.2 温度和载荷关系曲线图

图1显示了一系列温度和压力的关系曲线图，由（i）蒸汽温度，T_i,，冷启动时，（ii）外壁温度，与蒸汽顶盖处于同一时期，（iii）预估外壳温度时间的曲线，在其中头位于建筑，和(iv)蒸汽时间压力曲线。这个周期被称为现实周期。蒸汽温度，T_i,，是从一个热电偶连接到一个短管测得；外壁温度T_o，使用热电偶连接的厚壁部分的外表面的头测得。如图1所示，所测得的数据仅为第一个20小时可用；超过此，蒸汽、外头和外壳都以固定的速率冷却。

可以看出，蒸汽温度（图1中的蓝色线条）遵循以下模式：

（i）Ti开始从室温增长到398 ℃，时间持续超过2.4 h以上；T_i 在起初的8.3 h内保持在中间温度波动，大约平均在300 ℃。（这些波动是由于调温过程中，冷却水直接注入蒸汽流量，控制蒸汽温度的影响）。

（ii）Ti逐渐增加，在接下来的3小时中，一个稳定在约490℃的温度。

（iii）Ti停留大约在这个温度下约5.8小时

1. Ti返回到环境温度以13度每小时的速度，时间持续超过36小时。

外壁温度，一般滞后于蒸汽温度，例如，在加热（约6小时）后Ti，温度梯度高达150℃。在约5.5小时和14小时有个例外，当蒸汽温度的突然减少发生，导致在壁厚上产生较大的温度梯度，蒸汽温度和外壁之间的温度差高达100度。在最高的蒸汽温度（490度），壁温是比蒸汽温度冷约10度。在第开始的4.4小时内，蒸汽压力在0到17兆帕呈线性增加，然后保持恒定的压力，然后在该时间的头座温度最终稳定维持时间约为16.8小时。当头座进入它的冷却阶段时，压力降到零，持续超过1.4小时，这段视作为工厂关闭。两次H1和C1已在图1中标注出来；这段时间对应热梯度与较热的内表面（加热瞬态，H1 = 1.974小时）和较冷的内表面（冷却瞬态，C1 = 7.434小时）发生。蒸汽头是装在一个外壳，加热时间；外壳温度T1，（图1中所示虚线）最初是启动后环境温度和增加到325℃，然后在下面的一个保压时间内，蒸汽产生延迟，蒸汽温度进一步增加至约475℃。正如所看到的，蒸汽温度和外壳温度之间的这种滞后导致在启动过程中的头的内部和外部表面之间的显着的热梯度。

在图2中，有一个简化的代表周期（简称为代表周期）捕捉到真实的周期的显着特征，但没有如图1所示的复杂热瞬变。代表性周期的第一部分模拟启动至400℃并且包括一个设想的调温结果。蒸汽温度，Ti，增加到500℃后保持线性速率开始降温，在真实的压力–时间周期里，与已知的周期相同。为了进行在H1和C1时间的现实循环比较，H2和C2已在图2中标注出；这些与能够反映现实的周期瞬变时间加热瞬态（H1 = 1.974小时）和冷却瞬态（C1 = 7.4小时）有关。

图1. 基于头座数据测量的真实冷却的起始周期.

图2. 基于电厂头座状况模拟出典型的热力耦合头座损坏而设计的

具有代表性的起始周期

2.3 热模型

采用模拟热模型描述如下：

1. 在测量数据的基础上（如图。1和2）。随时间变化的蒸汽温度Ti（t）是指定的。
2. 随时间变化的外壳温度T1（t）是基于一个假设的轮廓（如图1），由工业经验可知，或者可以通过外壁温度测量得到。

（3）自然对流以头座外表面为模型。

（4）强制蒸汽对流以头座内部表面为模型。瞬态传热与温度相关的电导率和特定的热度数据，通过头座壁建模得到。

头座的材料经过检查是P91，P91的热力性质表1已经列出，数据来自于[12]。蒸汽侧对流系数由以下公式得到

其中h_i是蒸汽侧对流系数，k是导热系数，Nu是努塞尔特数由普朗特数所决定，普朗特系数和雷诺数都是[13]中的经验关系式

光滑的管道普朗特系数在0.5到1.5之间，雷诺数在10⁴ 到5 x 10⁶之间

其中rho;是蒸汽密度，u是蒸汽速率，d是内管直径，mu;是运动粘度。

这里使用的蒸汽速率是15米每秒（推荐的在管道运输中防止产生具有明显压降的速率[14]）。Hi数据如表2所示。 h_o是给定的介于预测和测量的头座的最佳表面温度。T_o表1可见。h_o的结果值为1800 W/m²。K是用来表示外表面的。

表 1. P91的温度传热特性 [12].

表 2. 测得的蒸汽侧对流传热系数

2.4 环状粘塑性模型

在等温下，P9的同相（IP）TMF和异相（OP）测试数据由[15]中所示，其温度范围在400–600度，应变范围在plusmn;0.5%内和应变率1 x 10^-3 s^-1内。P91热力试验数据也如[16]所示，覆盖广泛的温度、应变和应变率范围。在[16- 18]可以看到显著的影响效果，那就是P91环状软化现象。

在目前的工作中，材料模型也被称为双层粘塑性模型，如[ 18 ]使用的P91材料。该材料模型已成功地应用于高温形成的镍-铬合金工具[ 19 ]。双层粘塑性模型既具有率相关（粘塑性的）有具有率无关（塑料）材料的特性。弹塑性网络预测了材料的时间独立行为，同时弹粘性网络预测了材料的时间依赖行为，这是由于加载应变速率改变的原因。这两种机理的结合会产生应力r， 当达到屈服应力时会产生永久变形。粘性行为是粘滞效应所产生的。这个模型在有限元程序ABAQUS应用了。

这采用了两层模型的随温度而变的的变形和非线性运动和各向同性硬化循环塑性模型去验证与时间无关的性质和诺顿定律。对于双层粘

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[147585]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

您可能感兴趣的文章

• 流化床包衣造粒过程的监测与控制研究外文翻译资料
• 一种新颖的旋转流化床包衣细颗粒涂层的方法外文翻译资料
• 中国城市垃圾的处理和管理外文翻译资料
• 滤袋、气旋、和湿式除尘方法在真空吸尘器中的比较外文翻译资料
• 一个灵活的模型辗环机设计外文翻译资料
• 带有柔性转子的主动电磁轴承系统的识别外文翻译资料
• 柔性阻尼支承下转子振动特性实验外文翻译资料
• MapReduce:超大集群上的数据简化处理外文翻译资料
• 垂直循环式立体车库的停车与乘车调度优化外文翻译资料
• 高灵敏度、高稳定性的自温度补偿电涡流位移传感器外文翻译资料