
英语原文共 5 页
翻译一:
船舶操纵工况下船体的CFD仿真
摘要:船舶操纵是船舶流体力学的一种极端情况。该船在横摇和航向上经历了快速而大幅度的变化。为了评价帆船的性能,对帆船船体周围的水流进行了数值研究。它采用有限体积法和船舶运动方程。
关键字:帆船; CFD; 6自由度运动; 机动仿真
介绍
船舶流体力学计算流体力学(CFD)在近几十年来取得了显著的进展。目前已有一些商用软件包通过求解雷诺平均纳维-斯托克斯方程和运动方程来模拟海洋航行船舶周围粘性不可压缩流体。然而,这些应用大多没有考虑到帆船、高速游船等小船的大振幅运动。在小船上,由于动压力对船的姿态有很大的影响,我们必须模拟船在六自由度(6DOF)下的运动。
帆船的数值计算是CFD的一个极端例子。由于船舶的推进力是风在其帆上的推力,所以在巡航状态下,船舶具有跟角、偏航角和俯仰角。特别是在迎风航行中,我们必须进行跟踪操作,走曲折的航线。在操作过程中,在几秒钟内,船的脚跟方向快速切换约plusmn;30度。它需要同时控制舵和帆。
虽然完全处理这样的快速机动在理论上是可能的,但计算成本非常高。为了以合理的成本和时间获得仿真结果,必须对艇体的非定常大振幅运动和自由表面变形进行简化。Roncin和Kobus[1]对两艘帆船进行了动态赛艇仿真。利用拖罐试验的实验数据,对任意姿态角作用于船体的流体动力进行了估计。Formaggia等人使用势流求解器和RaNS求解器求解了包括自由表面效应在内的船舶动力学问题。由于船舶非定常运动时的流场随时间变化,且具有复杂的特性,在实际应用中应采用较大的简化。Akimoto[3]利用运动网格系统对一艘航向变化的帆船进行了非定常流动仿真。在模拟过程中,通过网格变形实现了自由曲面的变形。在自由曲面变形较大时,处理能力有限,但计算量小,有利于长时间的非定常运动船舶仿真。
数值处理
本研究的目标是在不进行拖曳试验的情况下,对新设计的帆船进行快速评价。为此,我们将使用Akimoto[3]的非定常帆船仿真。仿真的主要部分是船体周围水流的RaNS求解器。为简便起见,采用三维机翼理论模型对帆和舵上的流体动力进行了计算。
图1为本仿真的计算网格。它是O-O型结构网格适合于潮湿的水面面积的船。虽然船身表面的速度边界条件为无滑移,但船身表面网格根据船身的旋转运动在船身表面滑动。该处理避免了计算网格的大变形。目前的网格尺寸为50times;30times;30。
图1计算网格与船体表面
采用RaNS法和有限体积法对船体周围流动进行了数值模拟。湍流模型是由Baldwin-Lomax模型和子网格尺度模型组合而成。采用显式一阶欧拉方法对船舶运动方程进行数值积分。
(a)
(b)
图2船体姿态与自由水面快照,前视图(a)、俯视图(b)
自由曲面网格的变形是由以下运动学和动力学条件决定的。
(1)
and(on free surface) (2)
这里h是自由曲面的局部高程,Fn是弗汝德数,n是自由曲面的单位法向。向量, , 分别为流动速度、移动网格速度和自由曲面网格点位置。Akimoto[3]利用实验数据对模拟的船体表面压力分布和波浪剖面进行了验证。所测得的运动条件仅为航向变化4度。在仿真实际机动条件时,提高了模型的稳定性和精度。
图3航向变化试验中姿态角的时间历程
结果与讨论
在模拟中,我们只控制舵和帆的角度。所有姿态角的偏航,俯仰和横摇都是运动方程的结果。舵控制程序是一个简单的比例微分(PD)反馈控制器,使用船的速度矢量作为控制的期望值。假定风帆力与视风垂直(相对于船的风速)。风帆的控制只是指定风帆将向哪一侧展开,以及风帆是完全打开还是关闭。
图2显示了船身姿态的快照图像。由于船体网格点在水面上滑动,即使在大振幅横摇时,结构网格的变形也不显著。
姿态角的时间历程如图3所示。当无量纲时间t=1.5时,船开始运动并控制舵。为消除帆的不对称载荷,达到稳定状态,风压角为3度,横倾角为8度左右。当t=10.0时,艇改变目标速度方向36度,收帆转弯。当t=12.0时,帆在另一侧完全展开。控制程序仍在开发中,以完成跟踪程序。在今后的工作中,将对控制算法进行改进,并对跟踪运动进行验证。
结论
提出了一种基于船体周围水流RaNS仿真的帆船机动仿真方法。该方法采用单结构网格拟合自由曲面和船体在任意运动下的变形。目前,该系统需要改进机动算法来模拟真实的跟踪过程。该研究将为船舶设计研发和海洋休闲安全教育提供一个航海模拟器。
参考文献
K. Roncin and J. M. Kobus, “Dynamic simulation of two sailing boats in match racing,” Sports Engineering, Volume 7, Number 3, pp. 139-152, 2004
L. Formaggia et al. “Fluid–structure interaction problems in free surface flows: Application to boat dynamics,” Int. J. for Numerical Methods in Fluids, Special Issue: Institute for Computational Fluid Dynamics, Vol. 56, Issue 8, pp. 965–978, 2008
H. Akimoto and H. Miyata, “Finite-volume simulation method to predict the performance of a sailing boat,” J. of Marine Science and Technology, vol. 7, pp. 31-42, 2002.
翻译二:
帆船横摇稳定性控制
摘要:本文提出了一种动态控制帆船风帆的方法,以减小由风引起的横摇和横倾角。这个方法的主要目的是为了增强自动驾驶帆船的坚固性和安全性,同时也可以用来增加船员的舒适感。该方案由一个线性二次调节器()组成,该调节器控制风帆产生的力矩。根据风的相对方向和所需的力矩,查表选择最佳的帆角,以获得最大的前进加速度。仿真结果表明了该方法的有效性。
介绍
本文是Wille等人在2006所写文章的续篇。Wille等人在2006年提出的模型和航向控制器是本文理论的基础。建议先阅读另一篇文章,因为前一篇文章中的理论和方程将被直接引用(方程1 - 59),并且符号将被重用。
风帆的大面积提供了帆船前进的推力。然而,它也使船容易受到强风的袭击。由于大风,可能导致较大的横倾角,大量的横摇运动,并且在最坏的情况下,导致船倾覆。如果不能适应各种不同的天气条件,自动驾驶帆船将永远不会是一个可行的选择。系统的坚韧性是自动驾驶的一个重要方面。
本文提出了一种利用风帆控制横摇运动的方法。它将减少横倾角度和由风产生的横摇运动。控制器设计得简单有效,并且在反馈回路中使用的状态易于估计。
风帆控制器
1向前推力下风帆的最佳角度
风帆是用来为帆船提供前进动力的。在给定的相对风向下,有一个最佳的帆角,可以提供最大的前进加速度。因此,目的是创建从相对风向到风帆的最佳角度的图。我们首先定义了一种方法,来测量风帆在不受风速影响的前进方向上产生的力:
(60)
其中,为风帆在正向的波浪方向所产生的力(见(29)),为风帆所产生的力除以风速(相对于船)的平方。是和的函数,在一个给定的下,将有一个最佳的。
然而,不能自由选择;根据风向和,局限于一定范围内。这是因为我们只能控制一根绳子来限制,然而绳子只能产生张力。当风从右舷吹来,使得,并且在桅杆周围,由风帆产生的转矩一定是正向的(即正的攻角)。当风从左舷吹来,使得,并且一定产生负向的转矩(即负的攻角)。
下面的方程描绘了风帆稳态角度的上限和下限 ,,给出一个相对风向:
(61)
(62)
除了(61)和(62),仍然适用。也就是说,和。
通过所有可行且普遍的可以发现风帆最优的角度,试图在给定时,使最大化。这可以离线计算,并将结果存储在查找表中。在查找表中,在一个小的改变之间,对于最优,只有一个小差异,一个新的最优的发现,基于在两个数据点之间的线性化解决方案 (这是在线计算)。
2风帆的相对力矩
与我们定义纵摇方向上的相对力的方式相同,横摇方向上的相对力矩定义为:
(63)
其中,按每个最优的计算,并且添加到查找表。此后,这个的解决方案被称为无约束的解决方案,。
在应用控制律来减少横摇运动和横倾角之前,我们必须能够控制由风帆在横摇过程中产生的力矩。这是通过寻找新的最优来解决,尽管有限制的最大相对力矩在每个解决方案创建的。
为了产生需要的结果,我们会再一次执行像我们早先讨论的相同的遍历算法,但又伴随着限制:结果已经产生出一个相对于 67%或更少的力矩。此后,这个结果被称为。并且,将和它的相对力矩都添加进查找表。
然后,重复(或尽可能低)的约束的解,并命名为和。然而,添加了一个新的约束,即。更实际地说,这是为了确保,与之前的解相比,不同的解都将帆向同一方向移动。当我们试图在下一步中找到一个相对力矩的连续解时,这是很重要的。
图1 帆的最佳位置
然后我们就有了逆转这一过程所需要的一切。通过输入,我们找到相对应于相对风向的的解。然后,通过应用所需的的限制,可以发现基于介于由产生的不同的线性化的理想。
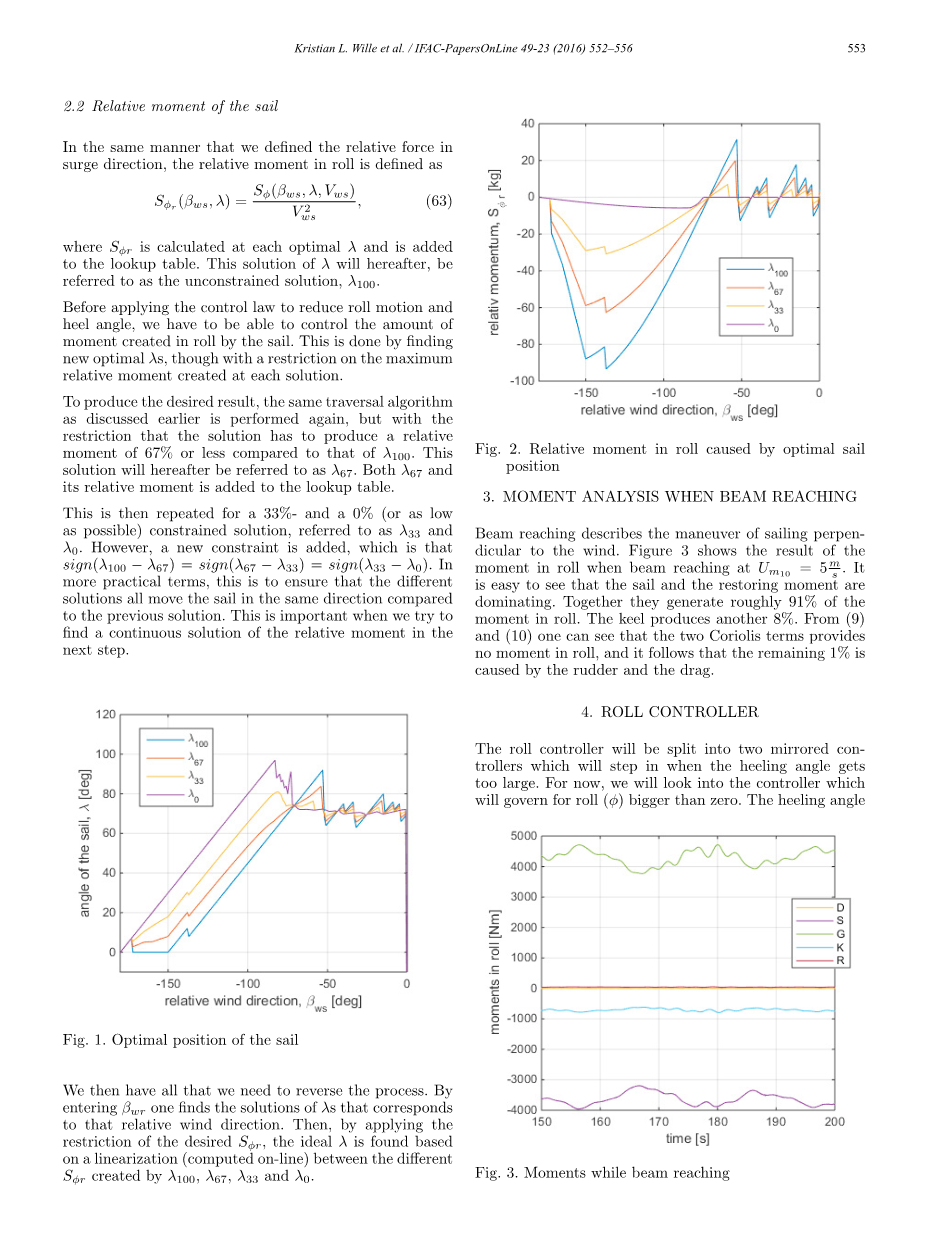
图2 由最佳船位引起的横摇时相对力矩
正横风驶帆时的弯矩分析
正横风驶帆时描述了垂直于风航行的动作。图3为正横风驶帆时时的横摇力矩计算结果。很容易看出,帆和恢复力矩占据了主导地位。它们总共产生了大约91%的转动力矩。龙骨产生另外的8%。从(9)和(10)可以看出,这两个科里奥利项在横摇中没有提供力矩,因此剩下1%的转动弯矩是由舵和阻力引起的。
横摇控制器
横摇控制器将被分成两个镜像控制器,当横摇角度过大时,镜像控制器将介入。现在,我们将研究控制器,控制器将使横摇()大于0. 为了舒适的旅程,倾侧角不应大于10度,因此,所需的横倾角设置为10度。
图3 正横风驶帆时的力矩
采用线性二次调节器()控制横摇运动。因此,第一步是建立一个关于一个平衡点的横摇运动的线性化系统,这个平衡点被选来当作所需的横倾角。线性化系统可以写成
(64)
(65)
图3和弯矩分析显示了哪些弯矩是重要的。两个最大的贡献来自风帆和恢复力矩。龙骨也提供了一些力矩,尽管由龙骨产生的力矩相当难以估计,因为它需要测量速度和侧滑,见(32)和(33)。然而,Wille等人(2016)认为,不需要的侧力((56)和(57))等于龙骨的升力。在(33)中,用替换显示,当的时候,由龙骨在横摇时产生的弯矩等于。是一个很好的近似值,当偏航角低的时候,几乎没有涡流。线性化后的恢复力矩(20)为
(66)
其中,是平衡点,且等于
(67)
将和由龙骨产生的力矩作为控制输入的一部分,对系统进行线性化,线性化后的系统模型只包含恢复力矩。矩阵A和B在线性化系统中变成
(68)
(69)
其中,定义为
(70)
添加积分控制运算来移除由系统线性化(即在给定一个,来计算最优的时使用的线性化)造成的错误和其他系统的不确定性。注意,在保持既定航向的情况下,龙骨产生的力矩相当稳定(图3),如果需要更简单的控制器设计,或者傅里叶变换难以计算,则可以通过积分控制运算来处理模型中不包含傅里叶变换的误差。
通过设置矩阵和,来调整控制器增益,其中,是由误差引起的二次成本的加权矩阵,表示使用执行器的二次成本。将调为, 将调为
(71)
然后利用函数在中计算增益。结果是。被手动调为2500。
当横倾角为负时,控制器是非常相似的。唯一的区别是,改为度,且重新计算为新均衡点(变化号)。在实践中,只使用一个控制器,在和之前的符号变换取决于横倾角的符号。
控制器只有在横倾角大于10度时才能打开。滞后现象也被用来避免控制器开关时太快,导致控制操作中断。重要的是要注意, 控制器不会创造相比于最优无约束的解()更多的弯矩,且横摇控制器比以前将不会进一步提高横倾角。因此,如果风速较低,且风帆不能提供足够的力矩使横倾角保持在10度,就必须采取措施避免整体积累。为了避免整体积累,积分作用不允许进一步成长,当,即没有力矩可以提供的时候。
如果横倾角小于10度,则继续使用控制器似乎有违直觉。虽然这可能是因为积分作用还没有达到一个稳定的值,而此时风帆对力矩的限制太大。限制横摇允许力矩的代价是减小前进方向的力,见图4,因此通常会降低帆船的
资料编号:[5122]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


