
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
桥式起重机箱型梁的设计优化
摘要 - 双桥梁桥式起重机被用于重型应用行业,本文中,框中键入一个起重量为150t,跨度32米,利用设计规则实现主梁详细参数化的基本设计。优化设计是用详细的三维有限元分析进行沿着梁的长度改变水平加强筋的数量,形状和位置与沿着竖直方向加强筋的数量和位置,以控制任何可能的屈曲,以最小可能的重量和安全应力和偏转。优化有两步要走。在第一步骤中,保持板厚度恒定的不同类型和添加加强筋数目的优化要清楚,在第二步骤中,第一步骤的最佳几何最大允许弯曲应力决定箱梁的厚度,高度和宽度以进一步优化,加入加强筋的作用在控制它的屈曲中突出显示。
关键词框,梁,优化,开销,起重机,屈曲,应力,挠度。
1,引言-高架起重机被用于操纵和从一个位置到另一个重物的转移,因此,它们在工业中的许多领域中使用,如在汽车厂和造船厂,[1,2]等。根据它们的主要操作规范,例如:起重机结构,重量和负载的类型,起重机的位置,几何特征和环境条件的运动的类型,其设计特点有很大变化。由于起重机设计过程中组件高度标准化,所以大部分的时间精力会花费在查阅设计标准的解释和使用。有很多对它们在承受静载荷和动载荷时的结构和元件应力的安全性的研究已经发表. Demirsoy已经研究[17] 桥梁结构和有限元分析(FEA)找到的位移和应力值的实体建模。18-20给出了实体建模技术应用于公路桥梁结构,并用有限元法对这些结构进行了分析,DIN tashenbuch和有限元法(联邦欧洲eacute;的de la公司)提供的设计规则方法和经验的方法和方程,是根据以前的设计经验和广泛接受的设计程序总结出的。DIN tashenbuch 44和185相关的标准集合与起重机的设计相关。DIN规范的一般状态的设计参数标准值。有限元法的规则主要有一个公认的规则集,以指导起重机设计师。他们包括确定外部载荷,选择起重机组件的标准。在本文中利用现有的DIN和F.E.M设计规则进行150吨的起重量和长32米跨度起重机进行箱式主梁的详细参数优化设计。优化设计是以最小的重量和安全应力和偏转,用详细的三维有限执行由沿长度变化的水平加强筋的数量,形状和位置元素分析加强筋的沿垂直方向的梁,数量,位置来控制的任何可能的屈曲。优化有两个步骤要走,在第一步骤中,不同类型和数量的加强筋是在优化中要搞清楚的,在第二步中,第一步骤的最佳几何,最大允许弯曲应力决定箱梁的厚度,高度和宽度以进一步优化,加入加强筋的作用在控制它的屈曲中突出显示:只有水平扶强材(研究-1)
只有垂直加强筋(研究-2)
水平和垂直加强筋(研究-3)
箱梁的参数优化(研究-4)
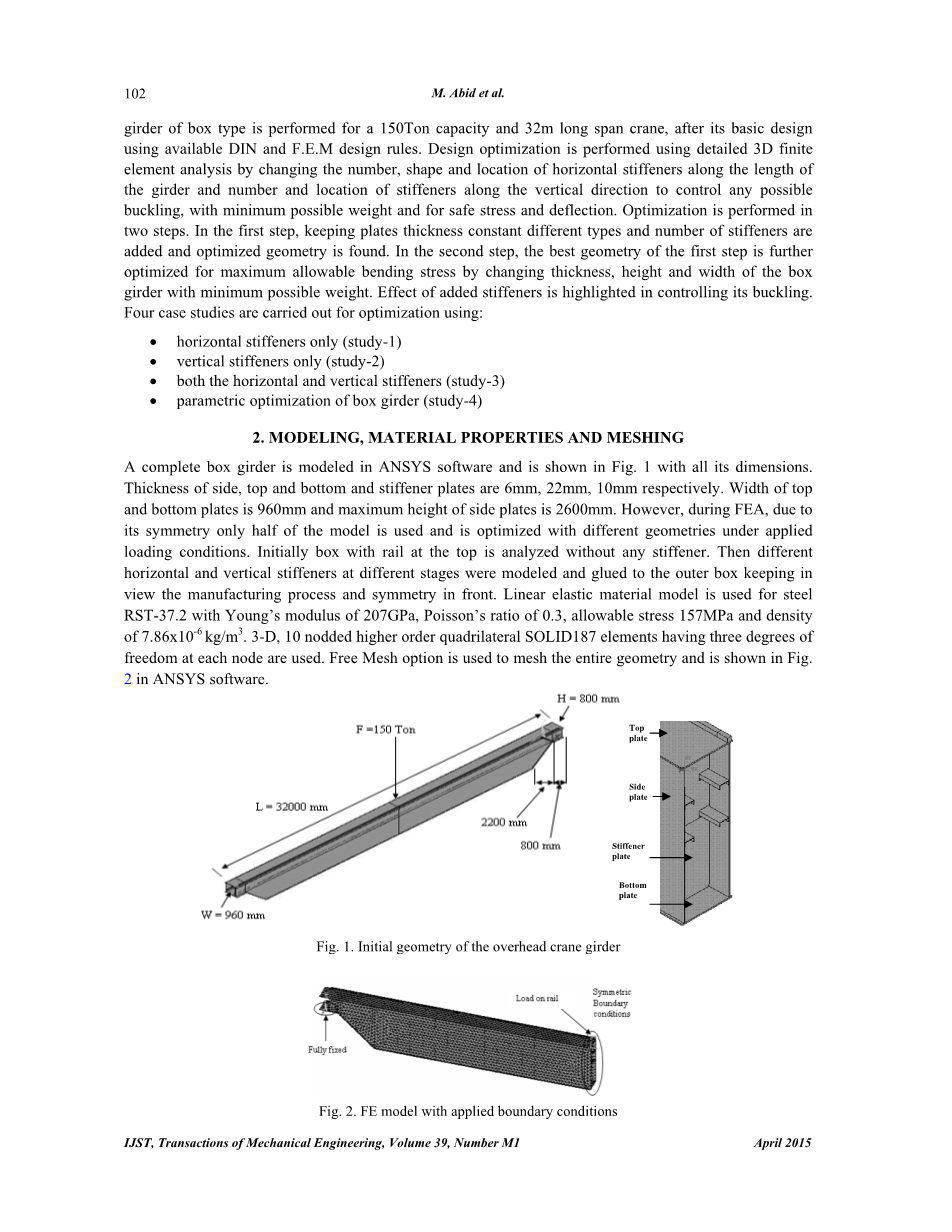
2.模拟,材料性能和网格。一个完整的箱梁在ANSYS软件建模,并在图所示。1的各个方面。
边厚度,顶部和底部加强板分别是6毫米,22毫米,10毫米。顶部宽度和底板是960毫米,侧板的最大高度2600毫米。然而,根据FEA,由于其对称性仅在模型的一半被使用,并且在施加负荷条件下使用不同的几何形状优化。最初在顶部轨道没有任何加劲肋被分析。然后不同的是在不同阶段的水平和垂直加强筋进行建模和胶合到外箱保持在查看在前面的制造工艺和对称性。线性弹性材料模型用于钢RST-37.2与杨氏模量207 GPa时的0.3泊松比,允许应力157兆帕和密度7.86x10-6千克/立方米。3-D,10允许有三度自由的高阶四边形SOLID187元素
在每个节点使用。免网状选项用于啮合整个几何结构,如图下所示。2 ANSYS软件。
使用倒置2 C形加强筋,在结果中没有差异,但是从制造的观点来看,这是不合理的。结论表2给出了梁最大弯曲应力的优化尺寸,最大排量,重量和体积,其中2 C形水平扶强材也同样伴随着17沿统一的高度和垂直加强筋沿支撑点4和C33的情况下变截面高度分布的情况。结果为最大弯曲应力和偏转分别绘制在图6和图7。
3边界条件。考虑吊车停下的位置和解除负载时起重机经常性的操作。在设计计算和有限元分析,没有水平力被认为可以作用于主梁。主梁被完全固定在其中,它被连接到托架的端部。用三点弯曲加载放法考虑手推车很小的两个车轮之间的距离。在6个节点上沿着轨道宽均匀施加载荷。对于不同的案例研究施加的负载被认为是与主梁的自重,并在下面相关章节中讨论。由于几何学的对称性,对称的板被施加的边界条件,如图2。
4 结果与讨论。在本文中37页箱梁优化的情况下弯曲应力,挠度和最低质量对应不同的类型,水平加强筋的数量和它们的不同的取向(图3)与不同数量的垂直加强筋的总结在表1。对于箱梁与无应力集中点没有加强筋的最大弯曲应力示于图4和5。
图3.(A,B,C)水平扶强材的不同取向
(a) (b) (c)
图4. 施加负载的梁由于应力集中在轨道上产生最大弯曲应力
箱形梁的优化设计
- 使用水平扶强材料优化。在这种情况下,优化仅仅是通过改变水平加强筋的数量,位置和形状进行。值得注意的是,有通过使用在最大偏转没有显着下降L形的加强件,但更好的结果是使用C形横加强筋来实现。最好优化结果(最大偏转=37.32毫米和最大弯曲应力= 176兆帕,梁的质量=16999公斤)可以使用400和1700毫米两个C字状的水平加强筋从顶板得到实现。分析还通过在ANSYS Workbench梁进行建模。使用内置元素,自由网格和消除应力集中点,最大挠度=36.24毫米和弯曲应力=165兆帕可确定的。但最大弯曲应力大于它可以忽略不计允许在所有的情况下的可允许的应力集中。结果为最大弯曲应力和偏转分别绘制在图6和图7。 图6
图7
- 采用垂直加强筋优化。在这种情况下,优化通过沿着梁的长度改变板加强件的数量和位置进行。据观察,通过从一到二增加垂直加强筋的数量,观察最大偏转从37.74毫米减少到34.79毫米。通过增加垂直加强筋的数量,观察到的相应减少是很小的。因为我们增加加强件1至7个,彼此相隔2000毫米的七纵加强筋,其挠度减小到34.79毫米,但观察到梁的质量(1042公斤)的增加。这接近于凸缘材料的许用应力,140兆帕的最大弯曲应力。用工作台和忽视的应力集中,最大偏转和最大弯曲应力分别降低至减小到29.52毫米和135兆帕,并且仍在允许的限度内。结果为最大弯曲应力和偏转分别绘制在图6和图7。
- 使用水平和垂直加强筋相结合优化。在这种情况下,分析是通过沿着梁的除了沿梁的高度相等位于两个C形横加强件的长度改变垂直加强筋的数量和位置进行。使用在1)这些结论,两个C形水平扶强材被用作最优化的结果。在这些情况下,垂直加强筋的数量增加时,最大挠度的值减小从34.24到34.06毫米,最大弯曲应力的值从增加139到140兆帕。有趣的是,要注意的是使用垂直加强筋3至7个,最大偏转和弯曲应力保持不变。但是,使用更多的垂直加强筋,梁的质量增加。垂直板这里使用,以避免侧向屈曲。在允许的限度内使用工作台模型和忽略的应力集中,最大偏转和应力降低到29.32毫米和131兆帕。此后,箱形梁,通过使用尺寸建模使得两个C形横加强件被放置625毫米和1250毫米远离顶板和第二十一垂直加强筋在梁的半模型。前四个垂直加强筋沿所述支撑和变化的横截面位于与剩余的17个垂直加强筋沿着梁的长度位于其中梁的高度是均匀的。垂直加强筋也使用和分析也是为了优化21和31。 除了位置,加强筋的水平方向也被改变,例如使用倒C形加强件等。使用除17垂直加强筋以两个C形加强筋沿所述梁的高度相等,的32.05毫米和最大弯曲132兆帕的应力最大偏转观察。使用工作台模型17垂直加强筋和去除应力集中,最大偏转和应力降低到28.18毫米和129兆帕。通过使用L形水平扶强除了垂直加强筋结果,使用2 C形加强筋,但在梁的重量略有增加也有发现。
- 箱梁的参数优化。在这个问题上,,梁恒,宽度,高度和箱梁的几何形状的厚度保持长度的许用应力的范围内尽可能小的权重做进一步优化。为了进行优化设计的定义以下变量和优化三个案例研究(C35-C37)的结果总结在表2中,其中最小质量的结论15588千克为C37。最大弯曲应力和偏转分别绘制在图为6和7。
设计变量:这些独立变量直接影响的设计目标,因此,宽度,高度和厚度的梁的板是设计变量。改变这些变量的对问题的解决方案有直接的影响。状态变量:这些是在更换设计变量而改变并且是必要的约束设计因变量。因此最大弯曲应力和位移矢量和是状态变量。目标变量:有必要尽量减少这些变量,因此,体积/重量的梁的最小化。
- 箱梁屈曲行为。屈曲是一个经受高压缩应力的障模式特征,其中,在故障的实际压缩应力比极限压应力,该材料能够承受较小的一个结构构件的突发故障。由于弹性不稳定性的这种不合理模式也被描述为故障。这种类型的故障应考虑壁结构的情况下,因为它们是特别容易屈曲和一般的设计必须针对若干不同类型的屈曲。是屈曲而不是受力因素决定了箱梁的性能。为了控制箱梁的屈曲,分两步进行优化。在第一步骤中,静态优化,即,引入固定尺寸和维持箱梁板的不同扶强材进行厚度恒定并得到最优化的几何形状。在第二步骤,动态优化,即,使用第一步骤的最优化的几何形状,只保留水平加强筋维常数,箱梁板的所有其他方面,顶部,底部,侧面和垂直加强筋进行了优化。梁的高度和宽度也进行了优化。为了控制箱梁的屈曲,使用进行了一些案例研究垂直加强筋和不同类型的水平加强筋,对结果进行了详细讨论。根据箱梁施加载荷和自重位移结果在标记角点底部,顶部和侧板取并示于图图8a,b和c。
a
b
C
图8.位置上(a)底板点; (b)顶板; (c)侧板(正面和背面)
在箱形梁的所有板,一些的角点的有在所有的情况下,几乎为零的位移。点B和C对所有行星的位移(UX)将保持零沿负载的应用的平面存在这两点,因此不存在沿着梁的长度这些点的位移。同样地,点A和D的位移(UX和UY)也几乎是零,因为包含所有这些点的部分在所有方向在底板的有限制。在所有情况下,点D的对正面和背面板的位移(Y)的几乎都为零。这是因为前板的点D是非常接近其在所有方向上的限制,因为这个区域是在末端支撑梁的区域。位移点A(OZ)和D为施加载荷的在所有情况下,因为包含这两个点的区域在所有的方向被约束的应用后底板为零。针对不同的板块位移可见的结果在下面的章节中讨论。位移YZ方向,即UY和UZ分别绘制在图9和10。
图9在箱梁板的角点位移对于不同的优化的情况下沿Y方向
图10在箱梁板的角点位移对于不同的优化的情况下的Z方向
1箱形梁的优化设计。点c为底部和顶部板的位移;b点个前板的y方向显示大约从21毫米增加到了31毫米。为底部和顶板点B的位移;和点B和背面板的下在Y方向是大约由41毫米减少到32毫米。这最终导致Y方向相同位移值几乎可以忽略和完成箱梁的稳定性。动态优化运行用于例35和37这里,箱形梁,和梁的宽度高度的板的厚度是待优化设计变量; 弯曲应力和梁的挠度状态变量直接更改为设计变量的变化,因此必须注意的状态变量将不超过157兆帕(允许弯曲应力)的允许的上限。目标变量是需要被最小化的梁的体积。点B和C的在底部,因为优化梁的尺寸,顶部和侧板Y方向的位移显示增加行为。但尽管如此,位移值在允许的范围内和梁的质量被降低。结果绘于图9。图11示出了用于不同的优化情况下,板的屈曲的比较。很显然,通过引入只有横向加强筋,板的屈曲不好控制。但一定程度上通过与水平加强筋沿着引入垂直加强筋,板的压曲被控制在最终的优化的情况下在。
图11,板的侧向屈曲,针对不同案例的比较
2在Z方向板排量(UZ)。点B和C的对顶板,以及正面和背面板显示几乎在所有的情况下,作为这四点的行为相同点B的位移(使用)彼此非常接近。几乎零位移这四点的在没有水平和垂直加强件的情况下被观察到。但通过引入在水平和垂直加强筋的,这些点的位移上升到这也是可以忽略不计的值,并且可以忽略不计的最后一种情况(C33)大约4毫米。
5结论。从详细的优化研究结果得出如下结论。
- 签订的最优化的情况下沿,沿统一的高度垂直17加劲肋和沿支撑4点和不同部分的高度均匀分布2 C形水平扶强材。从ANSYS Workbench中的模型取得的结果更准确,因为ANSYS模型有更形畸变的错误。
- 水平扶强材的方向不会使结果明显的差异。
- 最小偏转由等分的水平加强筋沿高度来实现的。
- 为了控制纵向和侧向屈曲,强烈建议使用水平和垂直加强筋。
- 加强筋的夹杂物通过优化板的宽度,高度和厚度的梁结论增加girder.A合理轻量化箱梁的强度
参考文献:
1. Oguamanam, D. C. D., Hansen, J. S. amp; Heppler, G. R. (1998). Dynamic response of an overhead crane syst
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[148707],资料为PDF文档或Word文档,PDF文档可免费转换为Word


