
英语原文共 21 页,剩余内容已隐藏,支付完成后下载完整资料
相对位移谱的阻尼系数分析
Julian J. Bommer and Rishmila Mendis
摘要
下一代的抗震设计规范,特别是采用基于性能设计的框架,包括基于位移而设计,而不是根据受力来根系。使用替代结构直接基于位移的设计方法,位移谱需要指定的大范围的响应时间和多个级别的阻尼。规范位移谱高于标称值5%的临界值一般很容易求出,通常与Eurocode 8和其他设计要素一样,通过改变一些系数与5%阻尼比相比。这些影响系数被定义为函数的阻尼比,或者在某些情况下,叫做响应时间,但它们不依赖预期的地震动。使用这两种预测方程在几个不同阻尼比下进行随机模拟,得到了不同阻尼的影响要素的水平随大小和距离的变化情况,反映了震动持续时间随阻尼比增加的关系。本文对把这些因素的影响纳入设计规范的位移反应谱进行了讨论
关键词:位移响应谱;基于位移设计;阻尼比;抗震设计规范
第一章 绪论
研究瞬时地震动引起的惯性力和结构的破坏之间的相关性,引起了基于位移抗震设计方法的发展和评估。在结构非弹性位移方面已经提出了非常多的计算方法,许多都是基于等效弹性系统的响应做出的。这些方法都是根据等效线性化,使用替代结构非弹性变形的概念建模,减少根据滞回能量耗散而通过增加水平的粘滞阻尼建模。
采用直接基于位移设计(DBD)方法把压力给了工程地震学家们,他们需要提供合适输入的长周期位移谱的一系列阻尼比。转换现行抗震规范的加速度谱变为位移谱通常会导致不可靠的长周期下的位移值,这与DBD紧密相关。
J. J. BOMMER AND R. MENDIS
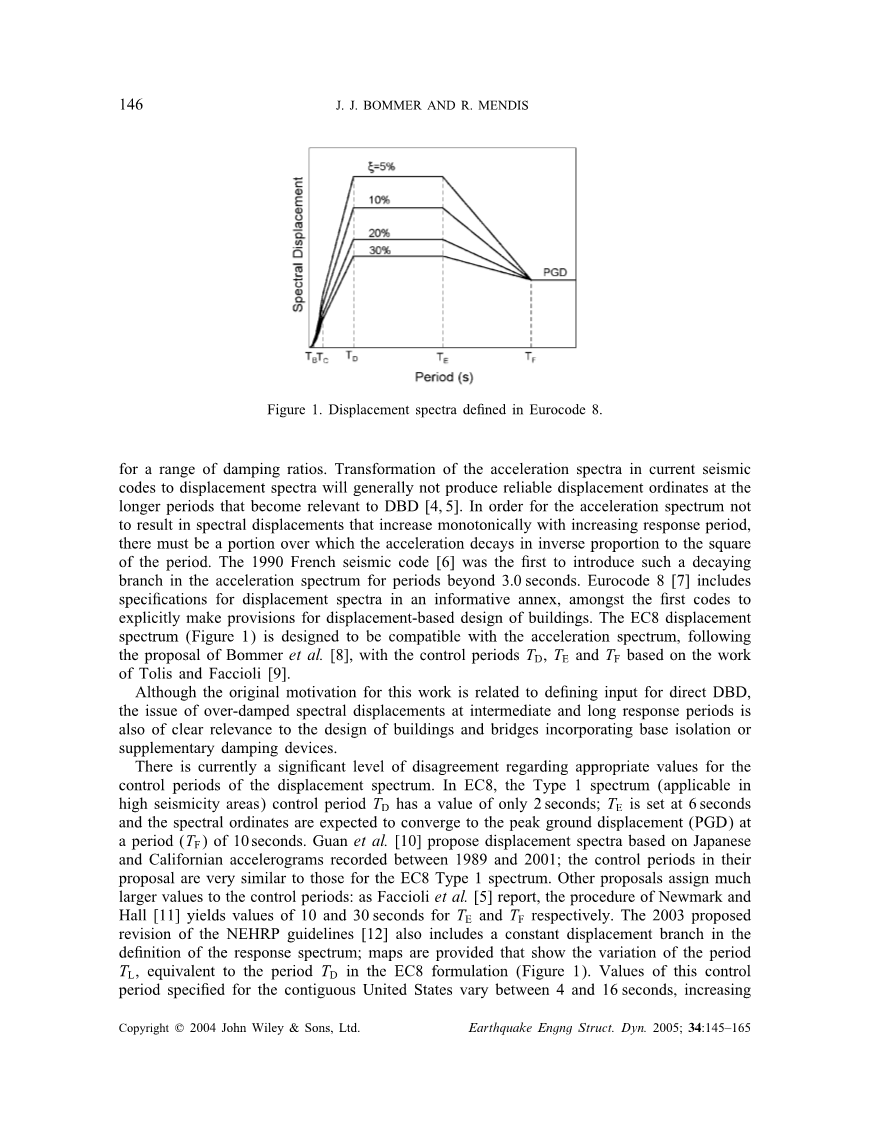
图1 位移谱Eurocode 8中的定义
为了加速度频谱不会导致随着位移谱而增加的响应周期单调增加,必须有部分加速度与周期成反比例衰减。1990年法国抗震规范第一个引入一个加速度谱衰减时间超过3秒的分支。Eurocode 8包含了一个位移谱规格的附件,它是第一个明确做出规定基于位移设计的建筑规范。EC8位移谱(图1)被设计成与加速度频谱兼容,紧随着Bommer提出建议之后,Tolis和Faccioli研究出了有控制周期Td Te和Tf的成果。
虽然这项工作的最初目的是给DBD输入定义作指导,但过阻尼位移谱在瞬时和长周期情况中对建筑物和桥梁的合并基础隔震以及附加阻尼装置也有明确的联系。
目前一个重要的分歧是为控制位移谱的周期选一个适当的值。在EC8,I型谱(适用于地震频繁活动区域)控制周期TD的值只有2秒; TE设置在6秒,谱值预计将收敛于在地面位移峰值(PGD)的10秒周期(TF)内。关教授等人提出一种位移谱,是基于日本和加利福尼亚记录在1989年和2001年之间加速度图制成的; 控制周期在他们的提议中,非常类似于EC8 1型光谱。其它方案给控制周期赋予了非常大的值:就像Faccioli等人做的一样。文献【5】显示,Newmark and Hall分别给TE和TF设定了10和30秒的增益值。2003版NEHRP指南的修订建议还包括在反应谱定义增加一个恒定位移分支,图谱显示了周期TL的变化,与在EC8(图1)中的周期TD相同。控制周期的值记录了美国在周期4到16秒之间连续变化,它随着地震规模呈几何倍数增长;12秒的值对应于新马德里受地震影响地区和加州的主要断层,另外高达16秒的受地震影响的地区在卡斯卡底古陆俯冲带。目前有很多工作还没有完成,之后才能获得可靠的长周期位移谱。
EC8等抗震设计规范中,除了阻尼比为5%的位移谱以外的反应谱都是通过应用不同的影响因素改变阻尼比为5%的频谱得到的。扩展系数被定义为一个函数的响应周期和阻尼比。目前有几种不同的方案来研究这些扩展系数,本文的下一节将详细的叙述目前提出的那种系数才是对规范的应用最有用的。本文中采用的方法是探索之前提出的不同影响因素之间的变化,调查只通过响应周期和他们的阻尼比来界定是否有系统性的变化规律在其中是否是正确的
第二章 谱的折减系数
图2比较了频谱比率,在这种情况下10%阻尼频谱是标准的,从纽马克和霍尔[11]以及吴和汉森[13]的研究中可知,20%的阻尼频谱运行良好。这两项研究在非常短和非常长的周期内趋向统一,正如所预期的那样。这两项研究都是基于拟速度谱,同样也适用于位移谱。Lin和Chang[14]发现,当相对位移谱和相对加速度谱的比率产生相当微小的变化的时候(对拟速度和拟加速度谱也是如此),相对速度谱和绝对加速度谱会显示一个更明显的变化。lin和Chang[14]也指出,不同的阻尼值的频谱比一般都由位移谱确定,然后作为受力情况应用到加速度谱抗震设计计算中去。这种观点与本研究无关,因为我们最关心的是中长周期的位移谱的情况 。
在EC8,阻尼比5%频谱值可以按照更高的阻尼比等比例缩小,Bommer[8]等人用一个简单的表达式写出了关系:
(1)
图2 从Newmark和Hall[11]的两项研究中使用中位值得到的10%的阻尼特征
影响因素应用于在TB(加速度稳定阶段的开始)和TE(图1)之间的所有响应周期;在短周期和长周期系数呈直线增长直到在T=0和T=TF时达到1.0;图3(a)比较了频谱比的结果,标准化的5%阻尼比的位移反应谱是从lin和Chang[14]在超过1000个强震动的加速度记录的中值中选出的方程(1)的值。虽然两组曲线之间在长周期下有很大的不同,但这反映出得到长周期位移谱时,几乎会遇到的所有的不确定关系,以及在几乎所有的长周期下谱形的变化记录的敏感性。当然在超过对应于ec8中2到6秒之间平稳不变的位移谱的周期范围后,用lin和zhang【14】的结果来看还是合理的。
方程(1)是一个包含在最初的规范EC8[15]中的类似的表达式,最初的起源和
推导过程已不可考:
(1)
图3(b)比较了从方程(2)得到的比率和lin和zhang【14】用百分之84比例的谱分量得到的值。因为在周期从0直到6秒时,契合度都非常高,这可能是巧合,但是也可能给出了关于方程(2)起源的线索。我们相信,抗震规范中根据调整系数将5%阻尼谱调整到其它阻尼比应该基于中值估计,因为地震动运动预测的固有变异性已经解释了5%阻尼比频谱的不确定性。
图3。有关阻尼比5%的频谱比:(a) 方程(1)比较了lin和Chang[14]基于中位数坐标的值;(b) 方程(2)比较了chang与lin的基于84百分比坐标的值[14]。在这两个情况,EC8的频谱比已经用从类型1的谱和C级场地类别的控制周期获得了
从图3可以看出,使用基于百分比84会产生高阻尼比的低级谱,我们还不清楚的是,这样一个选择是怎么成为合理的安全设计的
Tolis and Faccioli [9]提出了一个有着三种变化的影响因素,他们的研究主要是基于发生在1995年Hyogo-ken Nanbu (Kobe)地震的记录。
在其他一些抗震设计规范中,有可选的影响因素,虽然看起来大多数规范的起草委员会并没有预想除了假定为5%标称值的阻尼比之外的阻尼比会应用于钢筋混凝土。1990年法国规范[6]和1994年西班牙规范[16]都包括如下的影响因素应用于加速度谱:
1983年葡萄牙抗震规范[6]和1984年印度抗震规范[6]同时包括多个阻尼比水平下的加速度谱图示,但不提供拓展系数。图4比较了从这些图表得到的比值,平均了周期范围(在这两种情况下周期的变化很小),和从方程(1)-(4)得到的比值。
2001年加州运输局抗震设计标准[17]允许阻尼从5%上升到10%,如果桥深受桥墩能量耗影响,并且期望能够像一个但自由度体系一样响应的話。位移谱可以使用以下扩展方程,最初是由Kawashima and Aizawa[18]推导谱坐标绝对加速度而得出的:
图4 从许多抗震设计规范以及Tolis and Faccioli [9]
的研究中得出的不同阻尼比值的谱折减系数
1997年版的统一建筑规范(哥伦比亚大学)[19]提供了在一系列离散阻尼值的设计地震隔离结构中得到的影响系数。这些系数,和那些从方程(5)中得到的值,都在图4中显示出来了。
如图4所示的曲线和特征值反映了一个重要问题,那就是在阻尼比5%的位移谱拓展应用到更高的阻尼值时会有很大不同。由于研究大概都是基于弹性分析的单自由度体系(SDOF)振荡器,或许有人认为没有出现发生很大变化的差异结构模型。用合乎逻辑的方式去探索产生分歧的原因,就是去调查影响因素基于地震需求特性的程度。
第三章 高级谱的影响因素
为了探索地震时的地面运动特征在不同阻尼的反应谱影响系数下的影响,有两个方式:第一,是使用真正的加速度图谱; 第二种是使用来自地震模型的合成加速度图谱。
为了确定不变的、包括了可感知变化的数据,换言之就是一直都是在强振动下的数据的模型,我们需要大量的数据记录,但是人们不可能找到除了一个特征外,其他特性都非常相似的记录。出于这个原因,我们采用地面运动预测(衰减)方程的方法去研究多种阻尼比下的反应谱,这源自对经验强震动数据的回归分析。这些分析都是由基于中值的方程得来,根据以前解释的原因,有效的提供了一个很好的方式去识别大量强震动加速度图的平均情况。采用了四组预测方程,其特点总结在表I。前两个方程是来自西方北美数据,最后两个是来自欧洲的数据, 并且Berge-Thierry等人[20]补充了加州的记录数据去改进近源覆盖下的高震级的地震。
如上所述,第二个选择是用地震模型来合成地面运动,用不同的地震参数探索谱影响因素的变化。我们利用Boore[25]的随机方法去验证从地震震级的影响去预测方程得到的结果。
在接下来的三个小节,我们将从震级大小的影响,震源距离和场地条件这些谱影响因素上推断那些已经被发现的方程 。在3.4节中,我们简要讨论了受近场破坏方向影响的特殊情况。
3.1 震级
使用表1中列出的四个预测方程,不同阻尼比的平均反应谱都是建立在离不同震级地震10千米远的岩石基点上的。对于每个震级,谱坐标值都是除以5%阻尼比的频谱和标绘的阻尼得到的(图5)。
一个一致的模式在所有情况下都被观察到了:当时间大于0.3秒时——也就是直接关联到DBD(基于等效线性化)的周期——增大阻尼比导致的位移谱减小的情况,随震级增高而增加。
表I。用于这项研究的地面运动特征预测方程。
注:1.由亚伯拉罕森和夏德罗克[24]所定义的距离测度; 2.PSV=拟速度反应谱,PSA =拟加速度反应谱,SD =相对位移反应谱; 3.因为之前的一些设计规范评审都比较仓促,低于5%阻尼比的值在这个研究中没有考虑,因为这不大可能与基于位移的设计有关。
图5. 20%阻尼比的与5%阻尼比的谱的变化(由Trifunac and Lee and Bommer 等人的地震方程得到)。
图6.谱在T=2s时的变化比率(相对于5%阻尼比的谱) 从表1的四个预测方程中由地震中值推断出
图6显示了影响系数的响应周期在2秒(Boore等人的方程包含的最长周期)时的变化情况,这是不同震级和不同阻尼比的建筑由4种方程得到的。用仿真模拟同样可以得到与10千米的测点在不同震级下的响应情况,使用的程序叫SMSIM[26]。随着震级的增加谱比率下降的趋势也都被观察到了,如图7所示。默认的来源,路径和站点参数在加州沿海同样用于模拟。
如图6所示的谱比值变化情况很显然是从一个方程到另一个方程不断变化的,虽然可能在某些情况下似乎不是很明显; 其中所示的曲线变化情况与Boore等人的相一致,这是将震级二次项引入方程的结果。
在图中震级达到8级时,方程就可以轻微拓展,略微超过他们方程适用性的范围。在地震震级从6升到7.5级时,对于30%阻尼比的反应谱,从Bommer等人的方程推断出的影响系数应降低15%。
3.2 震源距离
Trifunac和li [21]的方程包含了完全一样的在所有阻尼比下的谱值的衰减情况,因此谱比率随距离的变化不能被推断出来。其他三个方程表现出同样的趋势,就是在瞬时反应周期影响因素随震源距离的增加而减弱。这两个方程的说明如图8所示。
频谱比的变化随着震源距离的减小就表现的越来越敏感,这是根据Boore和Bommer等人的研究得到的结果,比率变化的最大的范围就是在最初的10-15KM震源距。从强震动的数据集和当中相对稀疏的近场记录,我们可以推断出频谱比在这些距离的推断应该谨慎一些。
不同大小和距离的综合效应对谱影响因素的影响是明显的:运用Bommer等人的方程,以及考虑在T=2秒时30%频谱到5%阻尼频谱的比率变化,可以发现,在5.5级地震,震源距5KM到震级为7.5级,震源距为50KM时,比率从0.68降低为0.51:减少了25%。
3.3 场地类别
四个预测方程都包含了场地条件作为变量,它们允许该参数参与频谱比影响的研究,如图9所示。
四个方程使用的是不同的场地条件方案。Trifunac和Li[21]把他们的数据划分为'基岩',“冲积层”和“中间层”三种,并且频谱比的减少非常小,在中间周期,从硬土条件到软土条件的表现是一致的。Boore和Bommer使用相同的场地条件理论,这基于30m的横波波速,用360m/s和760m/s标记不同级别之间的边界。从Bommer的公式得到的结果没有表现一致的模式,但是众所周知,很大一部分在欧洲和中
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[154098],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


