
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
使用C空间法的五轴刀具定向优化
摘要:
在五轴刀具轨迹规划中,避免碰撞是根本问题之一。一种两步框架被广泛用于刀具轨迹的生成中,即先确定C空间,然后在C空间中设计无碰撞的轨迹。本文提出了一种基于碰撞锥计算和立体投影生成三角网格模型的C空间计算算法。然后我们在每个CC点的自由区域采样,并使用基于图形的方法生成刀具方向。本文还介绍了一种用于找到更光滑的刀轴方向的差分图。实验结果表明旋转的加速度和速度都比Plakhotnik和Lauwers给出的加速度和速度更加平滑。
关键词:五轴加工;C空间;迪杰斯特拉算法;差分图;刀具方向
绪论
五轴数控机床被广泛用于自由曲面,例如叶轮和飞机零部件。由于比三轴机床多了两个自由度,五轴机床比三轴机床在质量、精度,甚至是其他各方面都具有更强的制造能力。然后,多出来的两个自由度在刀具的工件的碰撞检测和防碰撞上带来了更大的挑战。已经对五轴机器的防碰撞相关问题进行了广泛的研究,这些问题主要涉及碰撞检测技术及其在刀具轨迹规划中的应用。Boyse [2]研究了静态对象和沿着指定轨迹移动的对象的碰撞检测问题。Moore和Wilhelms [3]将问题划分为运动学问题和动态问题。某些代数方法用于精确确定两个几何对象的相对位置,例如,Wang等人 [4]给出了两个椭球分离的代数条件; Chen 等人[5]找到了两个规则表面交集的显示公式。在速度规划中应用碰撞检测,Bobrow[6]给出了一种在运动约束下机器人的时间最优插值方法。Timar等人[7]在每个电机轴的最大加速能力的约束下提出了一种用于一般样条曲线的时间最佳插值方法。张等人[8]用不同的方法来平滑加速度曲线。杨等人[9] 提出了一种用于具有限制弦误差的曲面工具路径的组合时间最优插值方法。
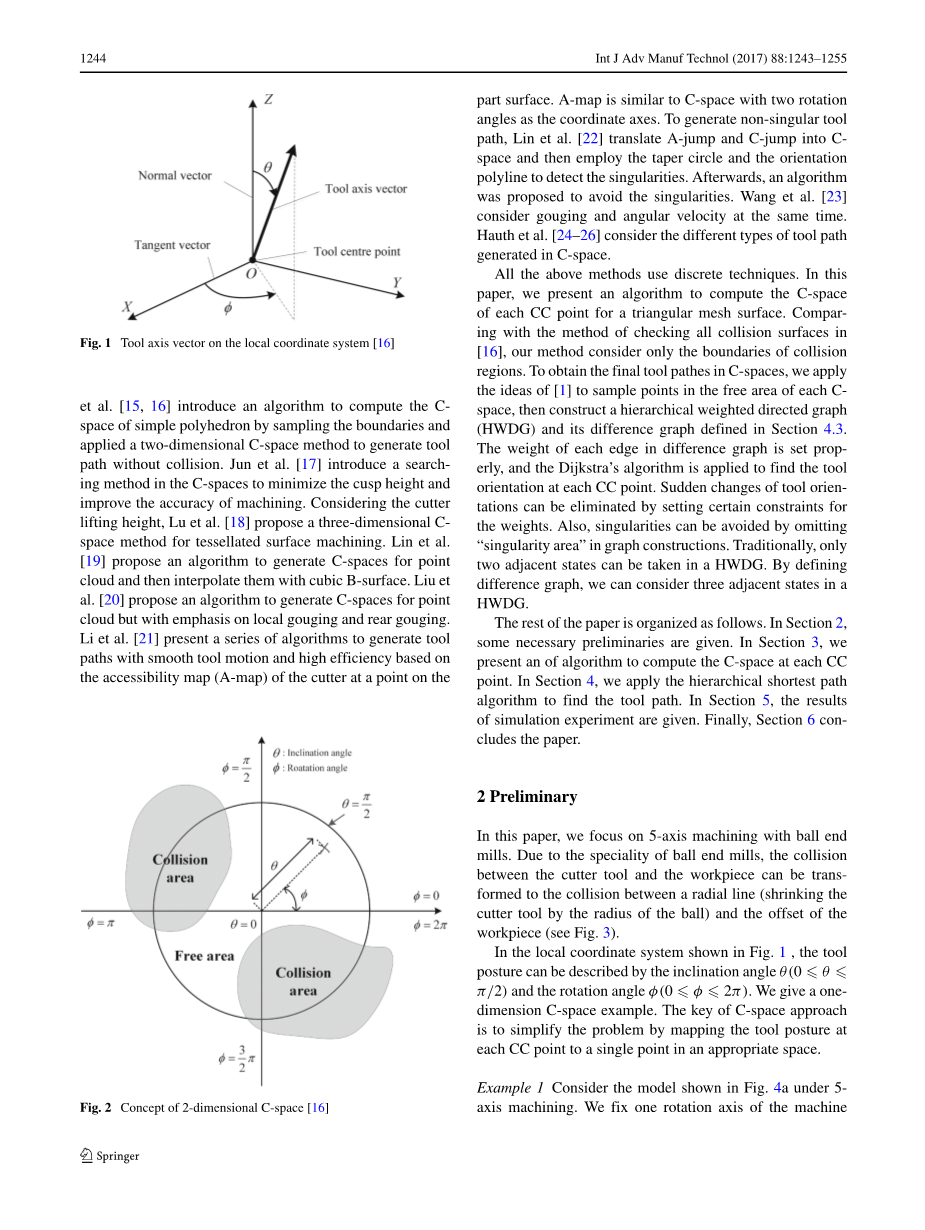
配置空间(C-space)的概念源自碰撞检测和回避中的机器人[10,11],并且后来被引入到CNC加工[12,13]。为了构建C空间,在每个刀具接触(CC)点(见图1)建立局部坐标系,使得每个CC点处的刀具姿势可以映射到theta;-phi;平面中的单个点 图2)。因此,可以判定碰撞区域和无碰撞区域的边界。碰撞区边界的计算是不太容易的[14]。Morishige等人引入一种算法来计算简单多面体的Cspace,通过对边界进行采样并应用二维C空间方法来生成没有碰撞的工具路径。Jun等人[17] 在C空间中引入搜索方法来最小化尖点高度并提高加工的精度。Lu等人提出了一种用于棋盘格表面加工的三维Cspace方法。Lin等人[19]提出了一种算法来生成点云的C空间的算法,然后用三次B面插值它们。[20]提出一种算法来生成点云的C空间,但重点是局部刨和后部刨。Li等人[21]提出了一系列算法,在基于刀具在零件表面上的点处的可达图(A-map)生成具有平滑刀具运动和高效率的刀具路径。可达图(A-map)和以两个旋转角度作为坐标轴的C空间相似。为了生成非奇异的工具路径,林等人[22]将A-jump和C-jump转换为C空间,然后采用锥形圆和方向折线现来检测奇点。然后,提出了一种避免奇点的算法。王等人[23]认为同时考虑气刨和角速度。[24-26]考虑了再C空间中生成刀具轨迹的不同类型。
图1
图2
上面所有的方法都运用离散技术。在本文中,我们提出一种算法来计算三角网格表面每个CC点的C空间。和[16]中检查每个碰撞面的方法相比,我们的方法只考虑了碰撞区域的边界。为了获得在C空间中最后的刀具轨迹,我们应用了[1]中的方法在C空间的自由区域采样点,然后构造分层加权有向图(HWDG)及其在4.3节中定义的差分图。差分图中每个边缘的权重设置正确,Dijkstra算法用于在每个CC点找到刀具方向。刀具方向的突变可以通过为约束设置权重的方式来消除。此外,通过在图结构中省略奇点区域可以避免奇点。传统上,在HWDG中只有两个相邻的状态可以发生。通过定义不同的图标,我们能够思考在HWDG中三个相邻的状态。
本文的余下部分组织如下:在第二部分中,给出了一下必要的初步措施。在第三部分中,我们提出了一种在每个CC点处计算C空间的算法。在第四部分中,我们运用分层最短路径算法来找到刀具路径。在第五部分中,给出了实验仿真结果。最后,在第六部分总结了此文。
初步措施
在此文中,我们专注于使用球头铣刀的五轴加工。由于球头铣刀的特性,刀具和工件之间的碰撞能够被转换为一条径向线(通过球的半径收缩刀具)和工件的偏置(如图3)之间的距离。
图3
在图1所示的局部坐标系中,刀具的姿势可以通过倾斜角度theta;(0le;theta;le;pi;/ 2)和旋转角度phi;(0le;phi;le;2pi;)来描述工具姿势。我们给出了一个以为C空间的例子。C空间方法简化问题的关键是通过将每个CC点处的刀具姿态映射到合适空间的单个点上。
例1:考虑五轴加工中图4a所示的模型。我们固定机床的一个旋转轴,因此只需要检查模型的横截面。下面是必要的概念。
·:工件坐标系中的
· :刀轴方向
·C点:其中一个CC点
·没有固定的旋转轴 :在和
设theta; = ang;BOA and beta; = ang;AOC,自由区域的边界能够通过以下两个等式确定:
当theta; = pi;/4时,的范围是()。注意,对于每个CC点,的可行值在自由区域形成一条线段。因此,所有的CC点形成的整个C空间就是图4中的阴影区域。
虽然例1中的C空间确实用解析几何的方式呈现出来了,但是C空间一般模型的精确计算在实际中一般是很困难的,因为将3D区域转变为其对应的2D角度边界就可能是很困难的工作。因此,我们接下来转向工件的多边形网格表示,并将示出如何为这样的模型计算准确的C空间。假设假设Msub;Rn(n = 2,3)是具有由,和表示的顶点,边和面的多边形网格M。因此,Nv,Ne和Ntau;是顶点,边和面的数量。
计算C空间
为了计算工件上CC点可行的C空间,我们先偏置了设计平面,因此刀具能够被转换成一条射线。图5通过红线示出了与偏移S工件接触的那些刀具姿态。CC点的可行C空间如图5b所示。
我们接下来会运用工件近似的三角网格模型M,拟合误差由加工精度界定。使任何两个相邻小面的外部法线共享M的边e为n1和n2。我们说e是位于碰撞区域边界上的边界边,如果 ,其中是从CC点C到点e的单位向量。碰撞锥是由CC点C和碰撞区域组成。如图6:
图6
通常计算碰撞区边界的方法是基于暴力算法检查网格每个面是否发生碰撞,见[17,27,28]。然而,这里我们改进条件(1)的网格模型,我们只需要搜索碰撞区域的边界与[16]中的过程相比。 我们称这些在条件(1)下计算的边是候选边界边,因为它们可能涉及冗余边(如图7.a),其可以通过立体投影消除(如图8)。
设SC为以CC点C为中心的单位球面,为C的归一化法向矢量,Ccircle为SC与C点的切平面相交的单位圆。我们通过将C点与候选边界边缘Sbdry。对于投影,我们首先使单位球面SC与碰撞锥相交,使得候选边界边缘Sbdry被归一化为是Sbdry。其次,我们通过方程式提取相对于的正球形边界Snew
因为,我们在单位球SC和从C到Sbdry的径向线的交点处只计算。最后,我们通过将Snew投影到在的SC的切平面,我们可以得到图8所示的Schain。
到现在为止,我们已经计算出了一组和CC点相关联的多边形(如图7b所示的实多边形)。为了找到碰撞区的最后边界。我们仍然需要提取这些多边形的联合的全局外边界。为了实现,我们应用了由多边形[29]给出的技术(参见图7b中的蓝色虚线多边形)。
我们现在通过图9总结计算C空间的整个过程并在下面给出了算法。
备注1:注意,实际的C空间边界很可能有突变。对于这种情况,我们需要细化工具路径,使得cc点足够密集,以产生C空间突然变化的尖锐特征。具体的,如果在第i和第i 1个CC点之间发生突然变化,则它将通过自然假设被反映在第i 1个CC点的C空间中,其中冲突区域将不时显现出来。在这种情况下,通过我们在下一节中介绍的刀具定向优化算法,在最终刀具定向中不会出现“突然变化的区域”
|
算法1 找到可行C空间 |
|
输入:三角网格M,CC点的位置和法向矢量 |
|
输出:一个可行的C空间 |
|
1.同条件(1),通过暴力方法计算边界边的集合Sbdry |
|
2.通过立体投影消除多余的候选边界边。 |
|
3.通过全局外边界提取外边 |
生成刀具方向
在本节中,我们的目标是生成平滑的刀轴方向,同时两个旋转轴的变化最小。假设进给速度是常数,这意味着刀具路径的长度| CiCi 1 | 在两个相邻的CC点Ci和Ci 1之间的加速时间可以被认为是加工时间。我们定义准速度和准加速度如下。
定义1:对于给定CC点Ci,一个旋转轴theta;的准速度omega;i为
,
其中是两个相邻的CC点的刀轴角度。
定义2:给定的CC点Ci的一个旋转轴线的准加速度是:
其中是和处刀轴的准加速度。
4.1 Plakhotnik和Lauwers算法概述
在[1]中,Plakhotnik和Lauwers对可行区域进行了采样,而没有刨削到每个CC点处的一些离散点,然后使用基于图的算法来获得最终的工具取向。为了简洁,我们将三个点视为在一条路径上如图10,然后我们假设在这些点的每个自由区域中仅抽样点, 如图11a所示。
图9 C空间生成算法流程图
Plakhotnik和Lauwers方法的概要是他们首先计算C空间的分层加权有向图(HWDG),如图12所示;然后使用适当的权重集,应用Dijkstra的算法来找到最短路径; 它们最终得到沿着刀具路径的刀轴方向。
图11
图12
图13
图14
在[1]中的方法将沿着给出的刀具轨迹的机器旋转角度最小化,但是三个相邻的角度没有考虑在内,这意味着旋转轴不够光滑。此外,他们没有考了两个相邻的CC点的间距,这意味着,他们考虑离散速度(两个相邻CC点刀轴方向的差别)而不是准速度。然而,刀轴方向有可能在在晓得区域产生突变(如图17),这会导致振动。例如,比较三个相邻CC点A轴的刀轴方向的两种情况,一种是,另一种是。假设在两个相邻的CC点的加工时间为1秒,在上面两种情况下的A轴的离散速度是一样的。前者A轴的加速度是0,然后后者的加速度是-10deg/S2。为了避免离散速度的突变,我们基于Dijkstra的算法提出了一种将刀轴方向的离散加速度考虑在内的新的算法。
4.2 我们的数学模型
在基于图表的方法中,目标是让刀具路径上总的角度变化尽可能的小,因此数学模型是:
其中代表刀轴方向的准速度,N是刀轴路径上的CC点数,是刀轴旋转的最大速度。
但是我们应该针对下面两个目标:一是将刀轴方向的准速度最小化,这样能够让刀具旋转实现尽可能小的平移;另一个是使刀轴方向光滑,针对于减少刀轴的振动。因此,这个多目标优化问题的数学模型是:
其中表示刀轴的准加速度。函数和能够被视为和,其中,,因此,不是一个连续性的函数,解决此问题最典型的方法就是用代替它,换言之,被取代变成了。此外,多目标优化问题非常难解决。因此,我们会引入惩罚参数lambda;将此问题变为一个单目标优化问题。因此,问题简化为:
用于优化问题的传统图方法仅考虑相邻CC点的两个工具姿态的关系,也就是说,如果我们将每个C空间中的采样点视为顶点,则边缘可以仅推断出在a轴中的准速度的信息 HWDG,但没有准加速度的信息。因此,我们在4.3节介绍一个HWDG的差分图,同时考虑准速度和准加速度。
4.3差分表
当计算给定刀具路径的C空间时,我们可以从CC点的每个C空间的空闲区域采样点。 网格尺寸由计算机的计算能力给出。图11显示了CC点第380,381和382个C空间自由区域的采样点。为了简单说明,我们假设在每个自由区域中仅采样两个点。然后,我们获得了一个HWDG G={V,E}其中V=是顶点集合,是边界集合,如图12a所示。
注意,如果我们删除准加速大于的边界,则自动满足最优问题(4)的条件。我们将以这种方式获得的图表示为具有的精确图,并且通过G = {V,E}来表示。
考虑到准速度的不同,我们可以将图的每个边视为顶点并考虑他们的差异。
设G*={V*,E*}。V *的每个元素表示G中的一个边
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[137060],资料为PDF文档或Word文档,PDF文档可免费转换为Word


