
英语原文共 9 页,剩余内容已隐藏,支付完成后下载完整资料
无限小退火法训练半监督支持向量机
Kohei Ogawa, Motoki Imamura, Ichiro Takeuchi, Masashi Sugiyama
半监督学习,学习的范式来自标记和未标记的数据在过去十年中已被广泛研究(Chapelle et al。,2006)。 半监督支持向量机(S3VM)或直推式SVM(Vapnik&Sterin,1977; Joachims,1999)是继承 “最大间隔”概念的受欢迎的半监督分类算法之一(Boser等,1992 ; Vapnik,1996; Cortes&Vapnik,1995)。 S3VM的基本思想是借助于未标记的数据来改进受监督的SVM解决方案(仅从标记数据获得)(Joachims,1999)。 S3VM成功的一个关键挑战是优化控制未标记数据的效果在分类器中的强度。
从算法的角度来看,S3VM尝试最大化标记和未标记数据的间隔,并将其作为将标记分配给未标记数据的组合优化问题(Joachims,1999)或非最优化问题,最大化未标记数据的间隔(Collobert et al。 ,2006)。 如Chapelle等人所述 (2007),实际上很难找到大问题的全局最优解。 因此,为了有效地获得良好的次优解,已经做出了很大的努力(Joachims,1999; Sindhwani et al。,2006; Chapelle,2007)。
Chapelle等人指出 (2008),迄今提出的大多数成功的S3VM训练算法实际上可以被视为退火方法(Korte&Vygen,2000; Hromkovic,2001; Kirkpatrick&Gelatt,1983; Colorni等,1991)。 也就是说,从原始监督SVM公式开始,解决了未标记数据的影响越来越强化的一系列子问题,以获得最终解决方案。 然而,在该退火程序中,退火步骤的数量与计算成本之间存在折衷。 因此,只有在增加计算成本的代价的情况下才能提高退火分辨率,这是目前S3VM实现中的关键限制。
本文的目标是超越这个权衡:我们提出了一种新的针对S3VM的训练算法,可以有效地执行无穷小级别的退火方法。技术上,我们的算法可以被认为是参数编程的一个特殊的扩展(Allgower&George,1993; Best,1996; Ritter,1984; Efron &Tibshirani,2004; Hastie等人,2004; Takeuchi等人,2009; Karasuyama等人,2012),并且当未标记的数据的效果不断增加时给出局部最优解的路径。 有意思的是,通过对S3VM局部最优性的必要条件进行分析,发现无限小退火步骤之后的局部解路径不连续; 解决路径实际上包含有限数量的突然跳转。
通过实验,我们证明,有限的退火算法倾向于产生比现有方法更少的计算时间的更好的解决方案。
我们在这里回顾了S3VM(Joachims,1999)。 假设我们给出了标注实例{(xi,yi)}iisin;L和未标记实例{xi}iisin;U,其中xiisin;R ^ d是输入向量,yiisin;{-1,1}是类标签。 决策函数:
f(x) = b w ^T·phi;(x) 在S3VM中被学习。其中phi;是特征图,w是要学习的参数,T表示转置。在S3VM中,偏置项b通常固定为b = 2r -1,以满足类 - 未标记实例的平衡约束, 参见Chapelle&Zien(2005)。
S3VM训练的问题被解释为组合优化问题(Joachims,1999)或非凸优化问题(Collobert等,2006)。 以下,我们回顾两种解释。
S3VM作为组合问题:基本思想是同时学习未标记和标记实例的决策函数,以最大限度地提高间隔:
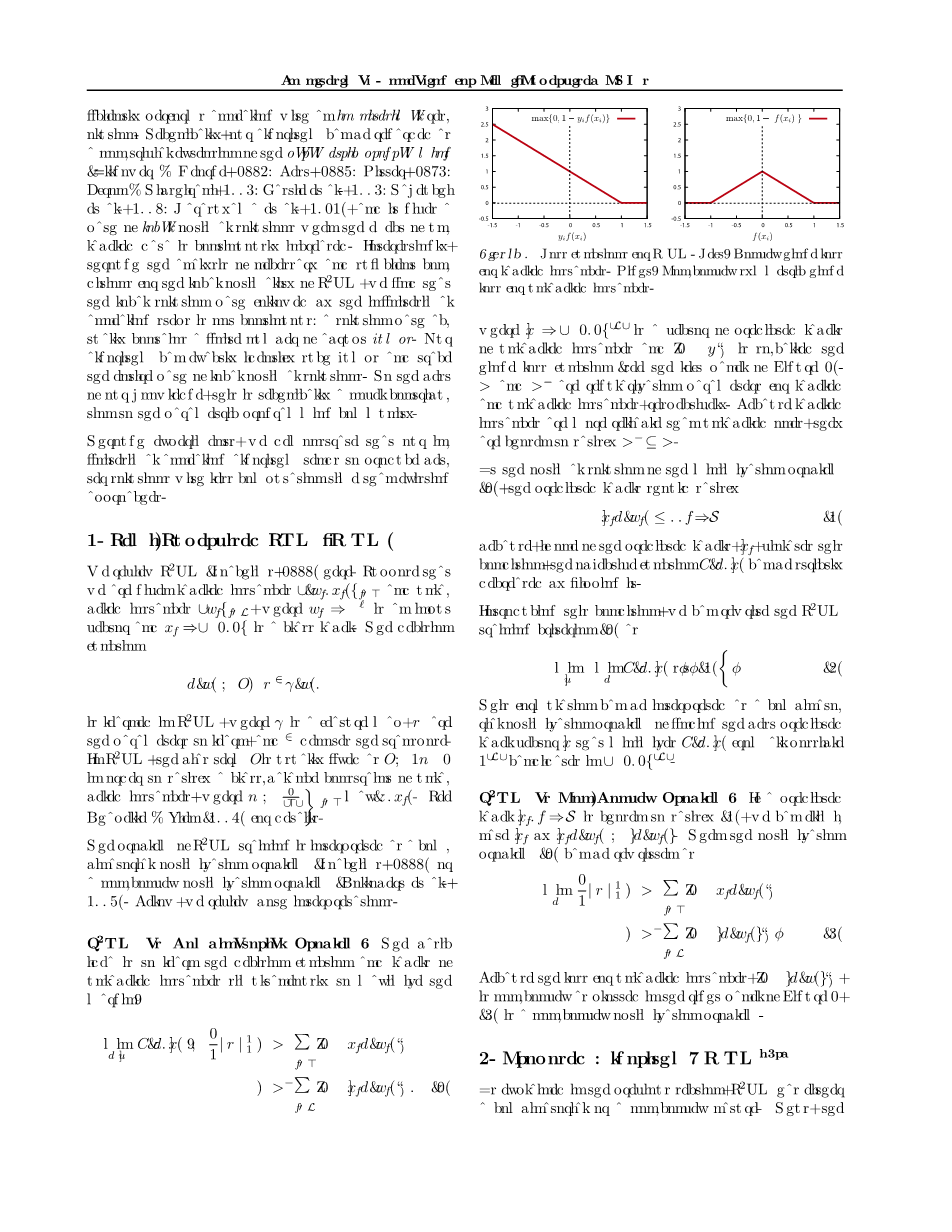
其中yisin;{-1,1} | U | 是未标记实例的预测标签的向量,[1-z] 是所谓的铰链损失函数(见图1左侧图片).C和C *分别是标记和未标记实例的正则化参数。 因为标记的实例比未标记的实例更可靠,因此选择满足C *le;C。
在最小化问题的最优解(1),预测标签应满足
因为如果预测标签之一yi违反了这个条件,则可以通过翻转目标函数J(f,y)来严格地降低目标函数。
介绍这种情况,我们可以重写S3VM训练标准(1)为:
该公式可以解释为组合优化问题,找到最小预测标签向量y,使得从所有可能的2^ | U | {-1,1}^| U |中的候选向量。
S3VM作为非凸问题:如果选择预测标签yi iisin;U以满足(2),则可以通过yif(xi)= | f(xi)|消除yi。 那么优化问题(1)可以重写为:
因为未标记实例的损失[1 - | f(x)|] 是非凸的,如图1的右图所示,(4)是非凸优化问题。
3.提出算法:S3VMpath
如上一节所述,S3VM具有组合或非凸性质。 因此,现有S3VM研究的实际目标是开发一种可以找到良好的局部最优解的算法(Joachims,1999; Sindhwani et al。,2006; Chapelle,2007)。
正如Chapelle等人所说 (2008),这些现有的S3VM算法利用退出概念来明确地或隐含地找到局部最优解:从监督SVM(C * = 0)开始,解决了增加C *的子问题序列。 在该退火过程中,退火步骤的数量与计算成本之间存在折衷。 这意味着只有以增加计算成本为代价才能提高退火分辨率,这是目前S3VM实现中的一个关键限制。
我们的目标是通过开发名为S3VMpath的S3VM的无限小退火算法来超越这一限制。 S3VMpath的基本思想是使用凸参数编程技术(Allgower&George,1993; Gal,1995; Best,1996)来计算C *isin;[0,C]的S3VM的整个解路径。然而,由于S3VM 是非凸的,我们的目标是计算局部最优解的路径。
为此,我们需要描述S3VM局部最优解的属性。 假设我们在固定预测标签y的凸多面体中定义了凸优化问题((3)中的内部优化问题),我们定义了以下概念:
定义1(有条件的最优解)
对于给定的isin;{-1,1}^| U |,我们提到凸问题的最优解:
作为pol(y)中的条件最优解,其中:
是由(2)中的约束定义的凸多面体。
粗略来说,S3VM的解决方案空间由许多这样的凸多面体组成。 正如我们将在下一节中展示的,S3VM解决方案空间具有以下两个重要属性:
bull;如果有条件的最佳解决方案在当前凸多面体的严格内部,则它是一个S3VM局部最优解(见图2和定理4)。
bull;如果有条件的最优解处于当前凸多边形的边界,则不是局部最优的,并且在其相邻的多面体中总能找到更好的解(见图3和定理5)。
这两个属性表明,S3VM局部最优解的路径不可避免地是不连续的,并且包含有限数量的突然跳转。 为了应对不连续性,提出的S3VM路径算法由连续路径(CP)步骤和离散跳跃(DJ)步骤组成。 更具体地说,从C * = 0开始,S3VM路径算法迭代CP步骤(遵循多面体中的局部最优解路径)和DJ步骤(一旦路径到达多面体的边界,找到另一个局部最优解 相邻多面体)直到C * = C。图4示出了算法的行为,其中红色表示CP步骤,而蓝色表示DJ步骤。
在下一节中,我们正式讨论了上述S3VM局部最优解的属性。 然后我们在第5节中描述S3VMpath算法的实现细节。
4. S3VM局部最优解
在本节中,我们正式讨论了S3VM局部最优解的属性。
首先,以下命题阐明了条件最优解与局部最优解之间的关系:
命题2 S3VM的任何局部最优解f是pol(y)中条件最优解,其中y满足yif(xi)ge;0,iisin;U。
这个命题是清楚的,因为如果一个解f对于y没有条件地最优,则在f的邻域存在一个更好的可行解。 注意,相反并不总是如此,即每个条件最优解不一定是(4)的局部最优解。 因此,我们需要澄清哪些条件最优解是局部最优的。
由于每个局部最优解对应于条件最优解之一,所以拉格朗日乘数理论(Boyd&Vandenberghe,2004)意味着局部最优解可以双重形式写为:
其中K是核函数,{alpha;i}iisin;LUU是拉格朗日乘数。 注意,在标准SVM中,第二项通常写为。 在这里,我们增加alpha;i以包括用于符号简单性的yi。
那么我们有以下必要和足够的S3VM的局部最优性条件:
引理3对于C *isin;(0,C),f为局部最优的必要和充分条件:
并且所有约束(2)都是非有效的,即:
引证3的证明在补充中给出。
局部最优条件的一个非平凡的部分非活动性条件(9)。 为了澄清这一点,我们将引理3改写如下:
定理4当且仅当严格在pol(y)的内部时,某个y的pol(y)中的条件最优解是局部最优解。
这个定理直接来自引理3,因为(8)是pol(y)中条件最优解的KKT最优条件的一部分,而(9)表示解不能在pol(y)的边界 参见引证3的补充说明细节)。 定理4表示的路径被保证是局部最优的,只要它停留在凸多面体pol(y)的内部,并且当路径到达边界的边界时,解不再是局部最优的 凸多面体(见图2)。
为了解释为什么在边界条件最优解f *(y)不能是局部最优解,让我们考虑“相邻”凸多面体pol(y0),其中
然后,如以下定理所述,pol(y 0)中的有条件最优解f * y0被保证是比f * y更严格的S3VM解决方案:
定理5令f *是在pol(y)中的条件最优解,并且假设yif * y(xi)= 0,iisin;S适用于非空集合Ssube;U.如果我们定义一个新的标签向量 y0由(10),即iisin;S的标签yi翻转,则条件最优解f * y 0 onpol(y0)满足
是一个比S3VM更好的解决方案。
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[26060],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


