
英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
边缘路径绑定:一种不太模糊的边缘绑定方法
马库斯·沃林格*
维也纳工业大学
丹尼尔·阿坎博dagger;
斯旺西大学
大卫·奥伯Dagger;
波尔多大学
马丁·诺伦伯格lowast;
维也纳工业大学
Jaakko Peltonensect;
坦佩雷大学
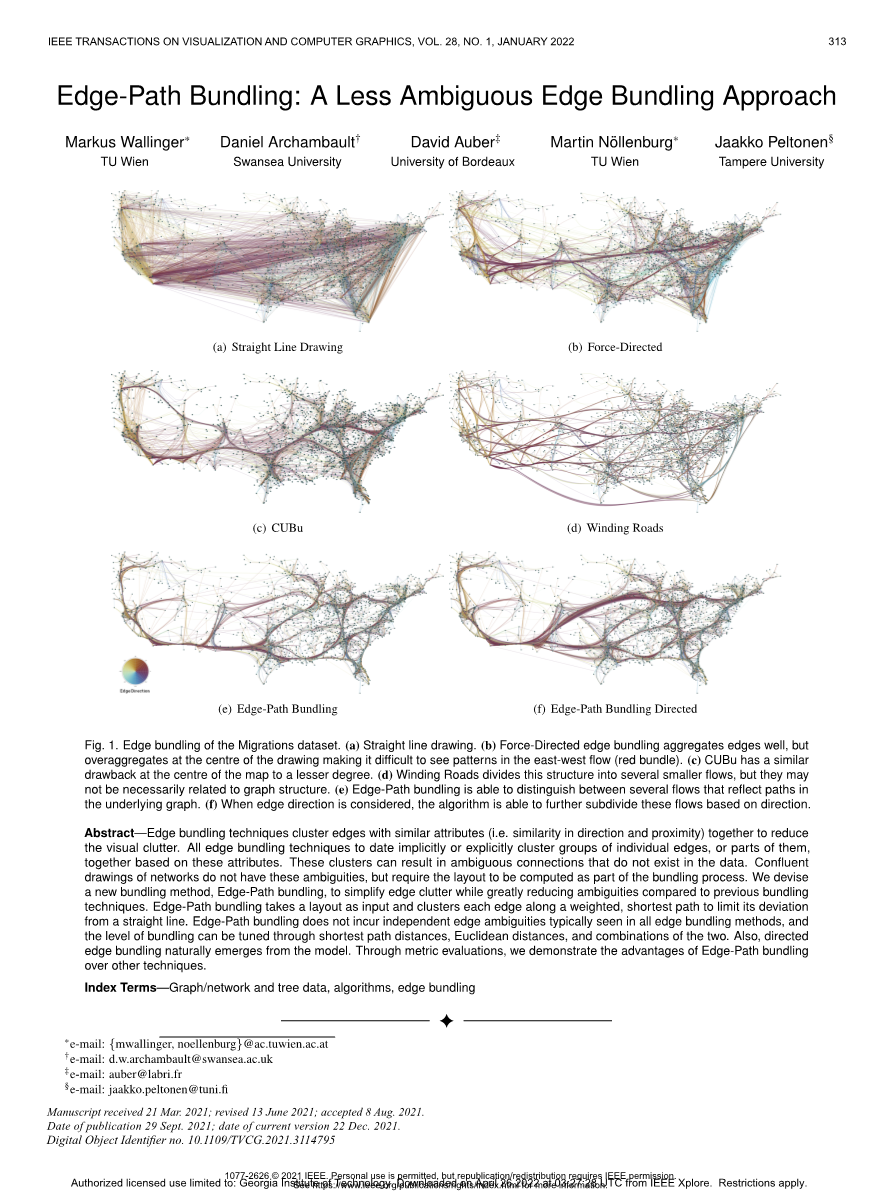
(a) 直线图(b)定向力
(c) 库布(d)蜿蜒的道路
(e) 边缘路径绑定(f)定向边缘路径绑定
图1。迁移数据集的边缘绑定。(a) 直线画。(b) 强制定向边缘捆绑可以很好地聚集边缘,但在图形中心过度聚集,使得很难看到东西向流动的模式(红色捆绑)。(c) 库布在地图中心也有类似的缺点,但程度较轻。(d) 蜿蜒的道路将这种结构划分为几个较小的流,但它们可能不一定与图形结构有关。(e) 边缘路径绑定能够区分反映基础图中路径的几个流。(f) 当考虑边缘方向时,该算法能够根据方向进一步细分这些流。
抽象边缘捆绑技术将具有相似属性(即方向相似性和接近性)的边缘聚集在一起,以减少视觉混乱。迄今为止,所有边缘捆绑技术都基于这些属性隐式或显式地将单个边缘组或其部分聚集在一起。这些集群可能会导致数据中不存在的不明确连接。合流网络图没有这些模糊性,但需要在捆绑过程中计算布局。我们设计了一种新的捆绑方法,即边缘路径捆绑,以简化边缘杂波,同时与以前的捆绑技术相比,大大减少了模糊度。边路径绑定将布局作为输入,并沿加权最短路径对每条边进行聚类,以限制其偏离直线。边缘路径绑定不会产生所有边缘绑定方法中常见的独立边缘模糊性,绑定级别可以通过最短路径距离、欧几里德距离以及两者的组合进行调整。此外,定向边缘捆绑自然地从模型中出现。通过度量评估,我们展示了边缘路径绑定相对于其他技术的优势。
索引术语图形/网络和树数据、算法、边缘捆绑
*电子邮件:mwallinger,noellenburg@ac.tuwien。ac.at
dagger;电子邮件:d、 w。archambault@swansea.ac.uk
——电子邮件:auber@labri.fr
sect;电子邮件:雅克o。peltonen@tuni.fi
手稿于21三月2021日收到;2021年6月13日修订;接受8八月2021日。
出版日期:29月9日2021;当前版本22日期2021月12日。
数字对象标识符编号10.1109/TVCG。2021.3114795
1077-2626 2021 IEEE。允许个人使用,但重新发布/再分配需要IEEE许可。
授权许可使用仅限于:乔治亚州INSTIETUETHTOPSF:T//wecwhwn。你好。哦。gD/PUOBWLINCALOTIONDSE/DRIGHONTS/Ainpdreixl.2h6tm,2L0FO2R2MAORTE0I3NF:o2r7m:2at8ioUn。来自IEEE Xplore的TC。限制适用。
- 1简介
自从引入[24]以来,边缘捆绑就接近集群组
基于相似属性将单个边组合在一起。原版WX
论文要求在网络顶部建立一个层次结构,但很快就发展出了将边缘与共享属性捆绑在一起的技术[36](例如,接近度和同一方向的移动[15,25,31,46])(见图1)。然而,所有这些方法都隐式或显式地对单个边或其部分(例如它们的像素)进行聚类,而与图形结构无关。这导致了图2(a)中所示的一种类型的模糊性,称为独立边模糊性:两条独立边可以聚集在一起,导致对底层图形中不存在的虚假邻接的感知。
合流图[16]考虑了一个非常类似的问题,并根据它们在双液中的参与对边缘进行聚类。因此,合流图形不会出现独立的边缘模糊。然而,合流图形对图形的捆绑明显较少,在屏幕上留下了大量的边缘混乱。此外,这些方法同时计算网络布局和捆绑。已经有很多尝试放松合流图形的严格限制,以实现明确的捆绑[10,57],但所有方法仍然要求在捆绑的同时计算布局。
在所有这些方法中,如果具有相似属性(通常是边缘斜率和接近度)的一组边缘或其部分(即其像素)对齐良好,则将它们捆绑在一起。然而,当对这些边进行聚类时,底层的图结构并没有得到充分考虑。在图1中,显示了一条直线图和三种流行的捆绑方法。力定向边缘捆绑[25]和CUBu[50]极大地简化了边缘杂波,清楚地显示了流动的方向。这在图形中心的网络(红色边缘)的东西流向中尤为明显。然而,不相关的边可以被拉到一起形成一个束,导致连接模式的模糊性。基于网格的技术,如蜿蜒的道路[31],将边缘分成更小的束,但这些束可以包含不相关的边缘。本文提出的边路径捆绑方法,用端点之间的最短路径捆绑边。因此,不相关的边不会被捆绑,所有捆绑都反映了图形中的一条基本路径。在无向版本中,现在很明显,中央水流分为两部分:一部分流向大湖区,另一部分流向德克萨斯州。在东海岸和大湖区也可以看到其他图表中看不到的更多细节。定向边路径捆绑显示,这些捆绑实际上由三条以红色表示的主流组成。在直线图中,这些流在某种程度上是可见的,但除了定向边缘路径捆绑之外,任何其他技术都无法显示模式;特别是,从加利福尼亚州到德克萨斯州的流量分为三部分。
本文介绍了一种新的边缘绑定方法,该方法不考虑单个边缘组、它们的像素或双色作为绑定的原语。相反,给定一个输入布局(即trailsets[36]),它将带加权路径的聚类边视为捆绑的原语。图中的每条长边被捆绑到边端点之间的最短路径(图2(b)和图2(c))。根据定义,边路径绑定不受独立边模糊性的影响,因为要绑定边,图中必须存在一条路径,但它的限制性远低于合流图形施加的规则。此外,该方法自然地表达了无向和有向边缘捆绑,而无需修改算法。我们证明,与合流图形相比,该方法具有更显著的捆绑效果,同时消除了独立的边缘歧义。
- 2相关工作
自从Holten[24]引入边缘捆绑[16]和Dickerson等人[16]引入合流绘制(confluent drawing)以减少图形中的边缘杂波以来,研究领域一直非常活跃,许多方法都是通过将具有类似属性的边缘或其像素聚集在一起而设计的。当将边缘聚合成簇时,边缘绑定的当前技术水平可能会产生独立的边缘模糊性(图2(a))。为了避免这种情况,合流图将捆绑限制为完美的双液,但通常施加的约束太过严格
u v
WX
-
- (a) (b)(c)
图2。独立的边缘模糊和边缘路径捆绑。(a) 在边缘捆绑方法中,两条断开连接的边缘可以捆绑在一起,从而导致(u,x)和(v,w)之间的错误连接。(b) 边路径绑定通过将长边与加权最短路径绑定来避免此问题。(c) 对于有向图,使用有向路径。
严格要求进行重大捆绑。
边缘路径绑定设计了一个必要的规则,在完全消除独立边缘歧义的同时实现高效绑定。直观地说,当一对断开的边(u,v)和(w,x)捆绑在一起时,在(u,x)和(v,w)之间可能会出现一条路径,其中根本不存在连接。此外,边缘路径绑定可以避免在没有绑定模式的情况下进行绑定。在图3中,独立的边被随机放置在立方体中,所有捆绑技术在该图中找到一种模式,而边路径捆绑和合流图则没有。边缘路径绑定没有这个问题,因为它只绑定特定布局中带有加权路径的边缘。虽然与边缘捆绑相关,但这是一种根本不同的方法,不适合这些类别。
边缘捆绑。自从第一批技术被描述以来,人们已经探索了许多捆绑技术[36],这些技术往往受到流程图工作[42]的启发。已经提出了许多技术,但所有技术都有一个共同的基本原理:将具有相似属性的边组聚集在一起。
边缘捆绑由Holten[24]引入可视化社区。在他的开创性工作中,通常通过树形图变体[13,30]将层次结构叠加在网络的顶部,并将簇层次结构的质心用作控制点,将边缘聚集到合并和拆分流中。不久之后,对层次结构的要求被消除,取而代之的是一种理想的属性,即将具有相似长度的类似方向的相邻边缘捆绑在一起。基于这一想法,人们创造了许多方法,包括使用三角形网格[15]、网格和四叉树[31,37]、力导向算法[25,40]、力导向算法,以及在力系统中编码的边方向,以及兼容性度量(如连接距离)[45]、稀疏可见性扳手[43],多层次聚类[21]。特定领域的集群和布局已被用于帮助捆绑过程[32,44]以及更通用的集群[47]。基于图像的[19,29,35,46,50,54]技术对单个边缘的像素进行操作。这些方法通过将所有边缘的贡献相加,创建一个在像素级计算的密度或相似性贴图,之后所有边缘沿贴图的梯度向上游独立平流。捆绑也被用来简化平行坐标图中的簇[41]。
边缘捆绑技术通过隐式或显式地聚集边缘组或其部分(即其像素),极大地减少了边缘混乱,并允许在网络中可视化否则将不可见的更高层流动模式。然而,所有这些方法都会在一定程度上受到独立边缘模糊性的影响。此外,正如调查[36]中所述,可以在没有模式的数据中创建随机模式。在本文中,我们寻求一种折衷方案:高效捆绑,大大简化了网络,同时完全消除了独立的边缘模糊性。我们通过将长边与其端点之间的加权最短路径捆绑在一起,而不是将多组边聚集在一起,来实现这一点。
合流的图画。合流图形在视觉上类似于边缘捆绑,但在设计上,它们不会出现独立的边缘模糊。合流丛的关键思想是,只有双圈可以被捆绑,即Kn,m子图。这保证了一个bundle隐含的所有连接实际上都存在于图中。在他们的起源-
-
-
- (a) 边缘道路,合流(b)受力导向(c)蜿蜒道路(d)库布
-
图3。噪声图的捆绑。随机放置的顶点(V=1000)通过完美匹配连接,导致E=V/2条断开的边。图中没有结构,也不应该有束(参见[36]图19)。力导向、蜿蜒的道路和CUBu给人的印象是底层数据中没有结构。边路径捆绑和合流图形找不到捆绑。
最后,从理论上讲,合流图不允许任何边交叉[16,28],因此一些图根本没有合流图。合流图形的变体,例如∆-从理论的角度研究了合流图[17]和严格合流图[18,20],展示了识别允许某些类型合流图的图的数学特征和NP完备性。虽然关于合流图的大多数结果没有提供算法或实现,但Dickerson等人[16]和Hirsch等人[23]提出并实现了一些基于检测派系和双联的启发式方法,以引入合流束。合流图形基于抽象图形输入,通常以组合方式解决图形布局和边绑定。因此,现有的融合绘制技术不容易应用于预嵌入网络的边缘捆绑。在本文中,我们设计了一种折衷方案,它不像合流布局那样严格,而是更有效地捆绑网络,以便更高级别的特征变得可见,同时减少拓扑歧义。
混合方法。许多论文以合流绘制方法为基础,并放松了该方法的一些更严格的限制,以实现更大的简化。Bach等人[10]探索了通过放松合流图形的严格平面度约束来减少模糊捆绑的方法。他们的方法计算功率图分解,并使用生成的层次结构来绘制和捆绑网络。郑等人[57]对巴赫等人[10]进行了扩展,基于进一步减少交叉和歧义的额外约束,创建了严格、有力的融合图形。
上述两种方法是第一次尝试放松合流图形的一些约束,以生成不那么模糊的边束。在本文中,我们介绍了一种新的方法,使用不同的原语,但找到了类似的折衷方法:在完全避免独立边缘歧义的同时,实现更大的捆绑。
捆绑质量的可视化和测量。除了捆绑算法外,还开展了大量工作,以设计度量标准,评估捆绑算法之间以及总体上的性能。已经设计了度量标准来测量信度[38,39]、熵[55]、测地路径趋势或直线距离的失真[26],以及量化简化的数据墨水比[48]。我们在评估中使用并调整这些指标。
Wang等人[52]给出了将图形布局中的歧义可视化的方法,包括捆绑。在这种方法中,边缘方向和邻近度的对齐(捆绑适用性的经典定义)用于突出图形中的模糊性。Nguyen等人定义了图形可视化中的忠实性概念:“基础网络数据和视觉表示在逻辑上是一致的”[38]。边缘捆绑歧义用于说明表示中的忠诚或缺乏忠诚。根据定义,我们的工作通过避免某些类型的歧义,提高了捆绑表示的可信度。
总结边缘绑定技术提高了图形的可读性,但也存在独立的边缘模糊性,并可能引入底层数据中不存在的模式。合流图和混合方法不存在独立的边缘模糊,但具有
作为捆绑过程的一部分,降低捆绑程度并计算网络图。因此,本文介绍了一种新的绑定原语(边到路径)和基于该原语的新绑定算法,该算法可以对布局进行更忠实的绑定[38]。
- 3边缘路径捆绑算法
算法1为我们的方法提供了伪代码。该方法出人意料地简单,只需要四个参数:网络G=(V,E)、G的图形DG、最大失真阈值k和边缘权重因子d。该算法创建了一个局部哈希集lock,该哈希集指示算法何时将边缘从
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[603409],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


