
英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
9高层建筑
9.1介绍
现在高度接近500米的高层建筑,深入大气边界层,它们的上层可能会经历大型风暴的最高风速,如热带气旋或温带地区的冬季大风。顺风、横风和扭转模式下的共振动力响应是这些结构所经历的整体结构荷载特征。极端的局部风压可能会发生在它们的侧壁上。
二战后建成的一批高层建筑刺激了边界层风洞发展,边界层风洞至今仍是许多国家主要建筑项目设计风荷载确定的最重要的工具。
本章将讨论高层建筑风荷载研究的历史、主要响应机理和现象,以及现有的分析和半分析技术。
9.2历史
无论是在风洞中,还是在整个规模,高层建筑或“摩天大楼”属于对风更敏感的结构之一,它们对风的响应必然会引起结构工程师的关注,并吸引早期实验人员的兴趣。
帝国大厦高380米,是40年来世界上最高的建筑,在20世纪30年代是三项重要研究的主题(Coyle, 1931;Dryden and Hill,1933年;Rathbun, 1940)。Davenport(1975)对这些研究重新进行了一些详细的评价。
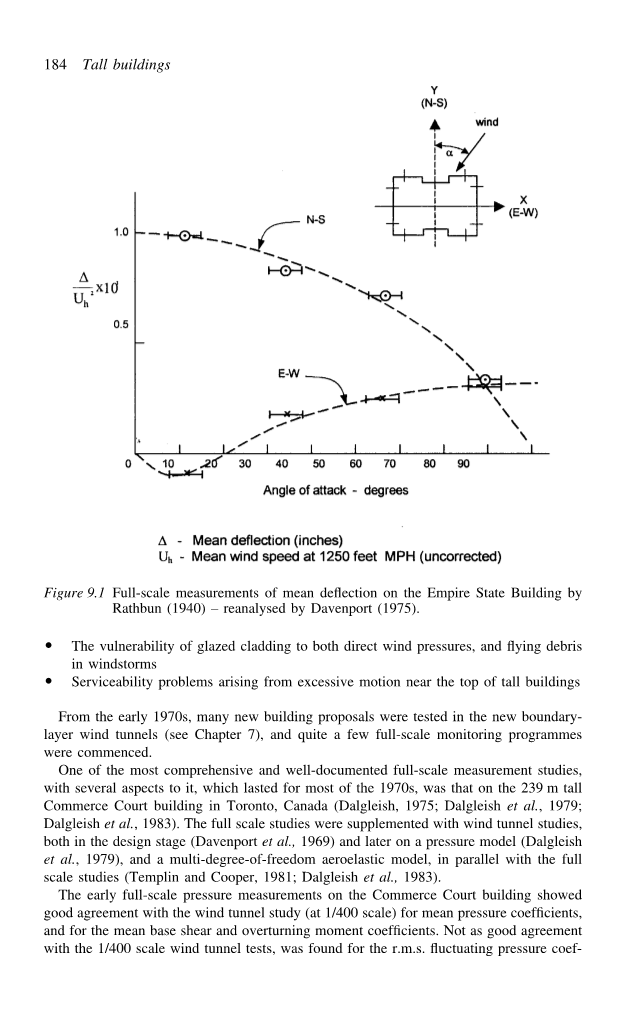
Coyle(1931)使用便携式水平摆来记录建筑物的运动。这清楚地揭示了共振动态响应的周期约为8秒。拉斯本(1940)广泛的全尺寸测量被达文波特描述为:“一个里程碑式的全尺寸实验”。用30个气压计和28个闪光灯测量了大楼三层的风压。风压系数表现出相当大的分散性,但明显比Dryden and Hill(1933)几年前在均匀流动的风洞模型上得到的风压系数低得多。Rathbun还对帝国大厦进行了挠度测量,使用了从86层延伸到6层的铅锤。这些结果(达文波特重新分析)表明,与南北向相比,该建筑东西向的刚度有显著差异(图9.1)。
在20世纪60年代和70年代,摩天大楼的建造再次兴起——尤其是在北美、日本和澳大利亚。当时人们对高层建筑的风荷载非常感兴趣,这种情况一直持续到20世纪末。
将出现的两个主要问题方面是:
图9.1Rathbun(1940)-Davenport(1975)重新分析的
全尺寸测量帝国大厦的平均挠度
- 玻璃覆层易受直接风压和风暴中飞溅的碎片的影响
- 由于高层建筑顶部附近过度移动而引起的适用性问题
上世纪70年代初,许多新的建筑方案都在新边界层风洞进行了测试(见第7章)和相当多的全尺寸监测方案已经开始。
在20世纪70年代,历经研究多年的加拿大多伦多239米高的商业法院大楼(Dalgleish, 1975;Dalgleish等,1979;Dalgleish等,1983)是其中一项最全面、记录最完整的全面测量研究。在设计阶段(Davenport et al., 1969)和后期的风压模型(Dalgleish et al., 1979)以及与全尺度研究平行的多自由度气动弹性模型(Templin and Cooper, 1981;Dalgleish等,1983)。
商业法庭大楼的早期全尺寸风压测量显示,平均风压系数、平均基底剪力和倾覆力矩系数与风洞研究(1/400比例)吻合良好。与1/400尺度风洞试验结果不一致的是某些风向的浅表(Dalgleish, 1975)的r.m.s.脉动风压系数。后来报道的风压测量(Dalgleish et al., 1979)显示,在更大(1/200)尺度的风洞模型上,使用精确校准的油管和风压测量系统,脉动风压和峰值测量有更好的一致性。商业法院大楼的全面风压研究强调了在分离的流动区域中短期峰值风压的重要性(大约在这个时候,在艾尔斯伯里的低层建筑的屋顶上也进行了类似的观察——第8.2.2节)。随后,对这些进行了详细的统计研究,以便应用于玻璃装载(见第9.4.5节)。虽然商业法庭的风压测量是高质量的,但他们缺乏一个独立的参考风压的风压系数——一个该建筑物层用过的内部风压系数。为了比较平均风压系数和风洞的结果,有必要在一个风压表接头处强迫一致,通常在尾流区。
加速度响应的全尺寸研究(Dalgleish et al.,1983)显示出以下特点:
- 一个方向(E-W)的扭转(扭转)运动叠加在摇摆运动上的意义。这是由质心和弹性轴之间的南北方向的偏心所引起的
- 对于来自不同方向的风,包括扭转运动在内的最终空气弹性模型与全比例尺数据之间的一致性一般较好
- 全面数据与加拿大国家建筑规范中关于侧风向和顺风向风加速的预测之间的合理一致。
尽管在建筑物顶部测量的参考速度和建筑物的动力特性(频率和阻尼)中存在一些不确定因素,显示的结果还是一致的。一个有趣的观察结果是,随着平均速度的增加,观测到的建筑频率明显下降,但这一现象尚未得到清楚的解释,但可能是质量效应的增加。
另一项重要的全尺寸研究是在伦敦18层的Royex住宅上进行的(Newberry et al., 1967),该研究对英国风荷载规范的发展具有重要影响。这项研究揭示了迎风侧墙的瞬态和脉动风压的一些方面。
上世纪60年代中期,美国科罗拉多州立大学(Colorado State University)为纽约世界贸易中心(World Trade Center)的双子塔进行了首个大型边界层风洞研究。这是在边界层风洞中进行的许多商业研究中的第一个,目前已有数千个。
9.3围绕高层建筑流动
高层建筑是中高宽比的钝体,第四章详细介绍了这种钝体周围流动的基本特征。图9.2为高层建筑周边边界层风场的一般特征。迎风面在驻点以下有很强的向下流动,驻点位于建筑物总高度的70 - 80%。由于来自上层的高速空气被带到街道上,所以底部的气流经常会造成危害。侧壁的分离和再附着与局部高压有关。背面为负风压区,平均风压较小,脉动风压较低。
图9.2风绕高层建筑流动
在下击暴流(1.3.5节)与天气风混合的极端风气候条件下,高层建筑的风荷载一般以天气风为主,下击暴流在高度50-100 m处达到最大值(图3.3)。
9.4表面风压
9.4.1风压系数
如前一章所言,风压系数将被定义为与建筑物的顶部平均风速的相对值,表示为。于是,根据式(9.1)、(9.2)、(9.3)、(9.4)分别定义均值、均方根脉动(标准差)、最大和最小风压系数。
(9. 1)
(9. 2)
(9. 3)
(9. 4)
在方程(9.3)和(9.4)中,最大风压和最小风压被定义为在给定的平均时间内的某点上的平均或预期峰值风压,在全尺寸模测量中这可能要花10分钟至3小时。在风洞试验中直接测量这样的平均峰值通常既不方便也不经济,人们提出了各种不同的统计方法。这些将在9.4.4节中讨论。
9.4.2矩形截面建筑物的风压分布
高层建筑墙体上的局部风压可以直接用于表面层的设计,而表面层一般由较小的支流区域支撑。
图4.15为边界层流场中高棱柱状面平均风压系数分布,高宽比为8,代表非常高的建筑物。
图9.3、9.4、9.5为较低的方截面长径比为2.1的建筑迎风面、侧风面和背风面的平均、最大和最小风压系数的变化(Cheung,1984)。在一个85米高的风洞模型上测量了风压;建筑是孤立的,即在高度相当的建筑上没有阻碍的建筑,来流是郊区地形上的边界层流动。Jensen数,h/z0,(见4.4.4节)的值约为40。
图9.3 平均、最大和最小风压系数-迎风墙正方形截面的建筑物-高/宽= 2.1
(Cheung,1984)。
最大值大约是0.8倍建筑高度。最大风压系数的高度略低于此。
侧壁(图9.4)与与前壁分离的气流相邻,产生强旋涡(图4.1和图9.2)。平均风压系数一般在-0.6到-0.8之间,与图4.15中高得多的建筑物的数值没有什么不同。与迎风墙风压不同,最小的负风压系数约为-3.8,出现在建筑物底部附近。在这种情况下,平行于侧壁的风向产生的负压最大。
背风壁上的平均和最大峰值风压(图9.5)也是负值,但通常是侧壁风压的一半。这堵墙当然是遮蔽的,并暴露在相对缓慢移动的空气中,在建筑物的近尾迹区。
9.4.3脉动局部风压的性质和概率分布
正如9.2节中所讨论的,在1970年代,全尺寸模型和风洞测量高层建筑风的风压,突出当地的负峰值风压,对于某些风向来说,可能发生在高楼大厦的墙壁上,特别是在侧墙在迎风角附近的位置和背风面。这些高压通常只发生在相当短的时间内,而且可能是间歇性的。图9.6(来自Dalgleish, 1971)显示了这些风压脉动的间歇性本质。
几项研究(如Dalgleish,1971;Peterka Cermak,1975)表明,风压脉动的概率密度分流地区高层建筑不适用于普通的或高斯概率分布(附录E)。尽管后者是非常适用于风的湍流速度脉动(见3.3.2节)。局部风压脉动的“尖峰”性质(图9.6)导致低于平均风压的五个标准差或更大峰值的概率密度比高斯分布预测的概率密度大几倍。图9.7通过对两座高层建筑的风洞测试的对比验证了这点。(Peterka和Cermak, 1975)。
图9.4矩形截面建筑物侧墙的平均、最大和最小风压系数-高/宽= 2.1(张,1984)。
图9.5方截面建筑物背风面的平均、最大和最小风压系数 -高/宽= 2.1(张,1984)。
图9.6全尺寸办公楼背风面的脉动风压记录建筑(Dalgleish, 1971)。
图9.7高层建筑分流区风压脉动的概率密度(Peterka and Cermak, 1975)。
高层建筑风压脉动的间歇性和非高斯性的结果是,在规定的时间内,在建筑物的特定位置测量的最大风压系数(例如10分钟)可能会有所差异,也可能因时间迁移而差异显著。因此,不能像高斯随机过程那样通过知道均值和标准差来预测它们(Davenport, 1964)。这导致许多不同的统计技术被应用来定义更一致设计峰值风压,这些将在9.4.4节中讨论。与之相关的是玻璃覆层对短时峰值荷载的响应特性。后者将在9.4.5节中讨论。
一项详细研究(Surry and Djakovich 1995)通过分析一般的连续等截面高层建筑模型的四个不同拐角的局部负压,表明拐角的细节不影响最小风压系数的大小,而真正造成影响的是风向角。最高峰值与旋涡脱落有关。
9.4.4测定局部峰值风压的统计方法
Lawson(1976)最初提出的一种简单的方法是利用风压脉动的父概率分布,从中提取一个指定(低)超越概率的风压系数。超越概率通常在1times;10minus;4至5times;10minus;4之间,后者由Lawson提出。该方法可以在风洞试验中“on the run”编程,相对容易;有时使用标准的概率分布,如威布尔类型(见附录C3.4)来拟合测量数据,并内插或外推到期望的概率水平。
Cook和Mayne(1979)提出了一种方法,将总平均时间T划分为16个相等的部分,在每个减少的时间t内保留测量到的峰值压力系数(最大值或最小值)。将I型极值(Gumbel)分布(见2.2.1节和附录C4)拟合到测量数据中,给出模式、Ct和尺度因子at。这些可以用来计算原始时间T的最大值(或最小值)对应的极值I型分布的参数,如下:
(9.5)
(9.6)
知道了极值风压系数的分布,就可以很容易地确定预期峰值或任何其他百分位数。Cook和Mayne(1979)提出的方法,实际上提出了一个有效的峰值风压系数Cp*,由:
(9.7)
Peterka(1983)提出用100个独立极大值在1 h内的概率分布来确定Cp*。
另一种方法是使用水平交叉统计数据。墨尔本(1977)建议使用风压水平(或结构响应)的标准化跨越率。选择标称通过速率(例如每小时10 - 4)来确定“峰值”风压的标称水平。
在给定的时间周期内,(I型)极压极值分布的参数也可以由水平过流率得到。水平交叉被认为是不相关的事件,可以用泊松分布(附录C3.5)来建模。
泊松分布给出了概率事件的数量n,在给定的时间范围内T,事件发生的平均概率nu;:
(9.8)
在这种情况下,“事件”可被视为特定水平的上升,例如超过特定风压水平。在时间T内,不超过某风压水平的概率p,等于低于最大值这一水平的概率p (T),即最大值的累积概率分布T。
因此,
(9.9)
假设水平x在时间T上的平均交叉次数为:
(9.10)
其中a和u是常数,
(9.11)
这是I型(Gumbel)极值分布,模式为u,尺度因子为a。
由式(9.10),两边取自然对数,
(9.12)
过程p(t)的I型极值分布的模态和尺度因子可以通过以下步骤估计:
绘制上升速度与水平的自然对数p画一条直线。由式(9.12)可知,斜率为(1/a),截距(p = 0)为(u/a)
从这些值中,估计出u和a, p的I型极值分布的模态和尺度因子。
9.4.5玻璃在风荷载作用下的强度特性
直接风荷载是高层建筑玻璃及其固定件设计中的主要考虑因素。然而,在某些城市,还需要考虑设计风产生的飞行碎片(第1.5节),特别是屋顶砾石的需要(Minor, 1994)。
如前所述
全文共6624字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[2693]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


