
英语原文共 21 页,剩余内容已隐藏,支付完成后下载完整资料
主干道信号协调与不均匀的双循环
摘要:在主干道协调中,大交叉口处的高交通量通常需要较长的周期长度以实现良好的双向进展。然而,这种长周期长度经常导致在交叉街道上交通量较低的一些小交叉口处的过度延迟。本文描述了为在主干道信号协调中实现不均匀双循环(UDC)以解决该问题而开发的优化模型。控制方案在一些小交叉点采用UDC,其中背景周期具有两个不同长度的子周期。开发了两个多目标UDC模型。基本的UDC模型最大化了恒定的双向带宽,并最大限度地减少了UDC交叉口路口的直行交通的平均延迟。然后通过最大化可变带宽并考虑行人需求来改进该模型。结果模型是混合整数二次规划(MIQP)问题。数值实验和案例研究模拟的结果表明,UDC控制方案可以大大减少UDC交叉口的延迟,而不影响通过交通的主干道的进展质量。还为UDC实施提供了初步指导方针.
关键词:信号协调、双循环、带宽最大化、减少延误。
1.绪论
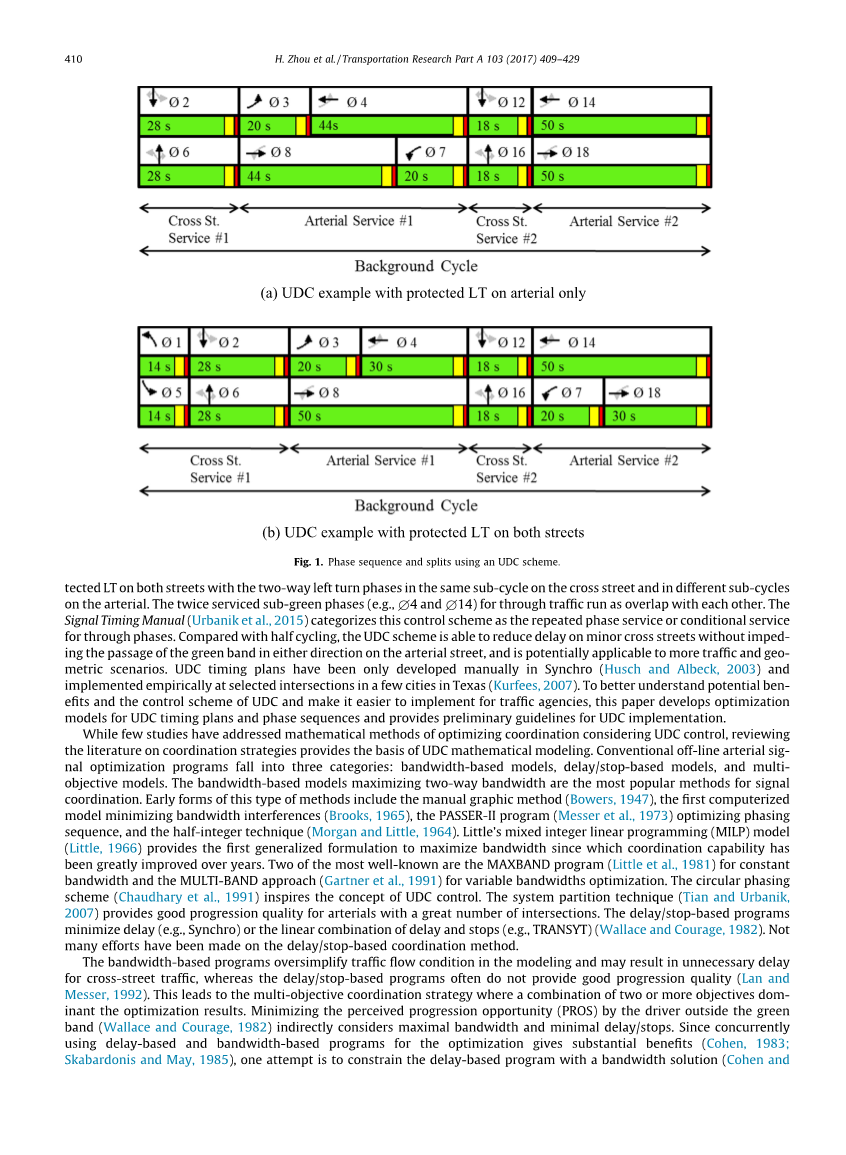
随着过去二十年交通量的增加,全国城市交通延误的总时数增加了一倍以上(USDOT,2015)。交通部门在高峰时段使用较长的周期长度(通常超过150秒)以产生更大的带宽,并在主要交叉口(两条道路上的高容量)之间提供足够的双向主干道进展,并通过减少停靠来减轻拥堵关键的交叉点。然而,较长的周期导致随机或均匀到达的较大延迟,并且使用长周期长度的常规主干道协调可能导致在主要 - 次要交叉点(小街道上的低容量)的小交叉街道上的驾驶员的过度延迟。交通部门在一些主要 - 次要交叉点使用了一半的背景周期长度,其中后半周期与前半周期重复完全相同的服务(定相序列和绿信比),以减少延迟。随着16相控制器的引入,Kurfees(2007)提出用更灵活的工具解决这个问题,即“不均匀双循环”(UDC)控制方案,其中循环中的关键阶段在后台循环中重复两次,但具有不同的相位长度。图1示出了使用UDC方案的相序和绿信比的两个示例。
图1中所示的UDC方案通过两次变动(通常具有不相等的相位长度)实现,并且通常在每个背景周期(如果有的话)在次要交叉点处实现左转保护相位。图1a中的UDC示例在交叉路口上的主干道和允许左转(允许LT)上保护左转(受保护的LT),并且在相同的子循环(子循环#1)中提供受保护的LT阶段。而不是在第二个子循环中。图1b中的UDC示例在两条街道上保护LT,在交叉路口的同一子循环中以及在主干道上的不同子循环中具有双向左转阶段。用于通过流量的两次服务的子绿色阶段(例如,pound;4和pound;14)作为彼此重叠运行。信号时序手册(Urbanik等,2015)将该控制方案归类为通过阶段的重复阶段服务或条件服务。与半循环相比,UDC方案能够减少小交叉街道上的延迟,而不会妨碍绿波带在主干道上向任一方向通过,并且可能适用于更多交通和地理公制场景。 UDC时序计划仅在Synchro(Husch和Albeck,2003)中手动开发,并在德克萨斯州几个城市的选定交叉路口实施(Kurfees,2007)。为了更好地理解UDC的潜在优势和控制方案并使其更易于为交通机构实施,本文开发了UDC时序计划和相序的优化模型,并为UDC实施提供了初步指导。
虽然很少有研究涉及考虑UDC控制的优化协调的数学方法,但回顾关于协调策略的文献提供了UDC数学建模的基础。传统的离线主干道信号优化程序分为三类:基于带宽的模型,基于延迟/停止的模型和多目标模型。最大化双向带宽的基于带宽的模型是最流行的信号协调方法。这种方法的早期形式包括手动图形方法(Bowers,1947),第一个最小化带宽干扰的计算机化模型(Brooks,1965),PASSER-II程序(Messer等,1973)优化相位序列,以及半整数技术(Morgan和Little,1964)。 Little的混合整数线性规划(MILP)模型(Little,1966)提供了第一个使带宽最大化的通用公式,因为多年来协调能力得到了极大的提高。两个最着名的是用于恒定带宽的MAXBAND程序(Little等,1981)和用于可变带宽优化的MULTI-BAND方法(Gartner等,1991)。循环定相方案(Chaudhary等,1991)激发了UDC控制的概念。系统分区技术(Tian和Urbanik,2007)为具有大量交叉口的主干道提供了良好的进展质量。基于延迟/停止的程序使延迟(例如,同步)或延迟和停止的线性组合(例如,TRANSYT)最小化(Wallace和Courage,1982)。对基于延迟/停止的协调方法没有做太多努力。
基于带宽的程序过度简化了建模中的交通流状况,并且可能导致跨街交通的不必要的延迟,而基于延迟/停止的程序通常不能提供良好的进展质量(Lan和Messer,1992)。这导致了多目标协调策略,其中两个或更多个目标的组合支配优化结果。最小化绿色频带之外的驾驶员的感知进展机会(PROS)(Wallace和Courage,1982)间接考虑最大带宽和最小延迟/停止。由于同时使用基于延迟和基于带宽的程序进行优化会带来实质性的好处(Cohen,1983; Skabardonis和May,1985),一种尝试是用带宽解决方案约束基于延迟的程序(Cohen和Liu,1986;刘,1988)。另一种尝试是正式制定多目标功能,以最小化主干道总延迟/停止并最大化带宽和主干道通量(Lan和Messer,1992)。目前的TRANSYT-7F和Synchro程序经过多年的改进,可以优化更多目标(Sabra等,2000)。请注意,两个程序都能够优化半循环但不能优化UDC。 Zhou和Hawkins(2014)首次提出了一种数学优化模型,该模型可以最大化带宽效率并最小化UDC控制下的总均匀延迟。带宽目标使用恒定带宽,需要MAXBAND程序的结果进行归一化。该模型不考虑行人时间需求。
本文采用了与Zhou和Hawkins(2014)提出的相似的基本模型结构,但在几个重要方面改进了它们的模型。 本文中的模型不需要MAXBAND结果来实现目标函数的归一化,从而提高了求解效率。 考虑可变带宽和行人定时以提高能力。 固定和驱动UDC控制的模拟评估结果被纳入初步指南,以更好地理解UDC的适用性。 本文的其余部分安排如下。 第2节介绍了基本和改进的UDC优化模型。 第3节涉及数值实验的设计和结果以及模型性能的模拟评估。 第4节总结了本研究的主要发现,并为UDC的实施和未来研究的可能主题提供了初步指导。
2.UDC控制的数学优化建模
用于UDC控制的数学优化建模包括基本建模,以在主干道协调中实现UDC控制,并改进基本UDC模型以考虑行人相位和可变绿波带宽最大化。 本文中使用的符号在第2.1节中列出。 一般来说,上标和下标中的字母“ɑ”或“c”表示主干道或十字路口; 上标中的字母“S”或“U”和下标中的“s”或“u”分别表示单循环和双循环交叉; 上标C1(C2)表示后台周期中的第一个(第二个)子周期; 上标中的字母“V”表示可变带宽最大化; 上标中的“T”表示通过运动; 上标中的字母“I”和“D”与整数替换和析取编程的约束有关。
基本的UDC模型
基本UDC模型采用MAXBAND程序中描述的带宽几何,并利用多目标优化策略来启用UDC功能。 该模型基于以下假设:
(1)普遍的交通状况不足;
(2)左转或通过运动不会发生车道堵塞或溢出;
(3)跨街道交通流量的到达和排放是不变的。
上述三个假设描述了适用的优化模型的稳定和重复的干道交通操作条件。 通常,通过使用长循环长度来满足欠饱和假设,以在临界(通常是主要 - 主要)交叉点处实现0.8到0.9之间的体积 - 容量比。 这种长背景周期长度有时会导致UDC方案可能有益的主要 - 次要交叉点的体积容量比小得多。与传统的单循环(SC)控制相比,UDC控制需要不同的环栅图设计,并且具有更复杂的带宽几何形状。 2.2节介绍了与MAXBAND编程不同的数学公式
2.2.1. 目标功能
所提出的模型考虑了两个目标:最大双向进展和在UDC交叉口的交叉街道上通过交通的最小总平均延迟。 为简单起见,延迟估计仅考虑均匀延迟并应用排队图来导出双循环交叉的延迟公式(因此,欠饱和假设)。
UDC下的背景循环具有两个子循环,每个子循环由主干道和交叉街道上的服务组成(例如,交叉街道服务#1和主干道服务#1在图1中形成子循环)。将包含出站绿色频带的子循环定义为第一个子循环C1,从而将没有出站绿色频带的子循环定义为第二个子循环C2。然后,在C1中通过移动的绿色分割和红色分割被定义为第一子绿色分割gC1和第一子红色分割rC1,并且相应地定义第二子绿色分割gC2和子红色分割rC2。对于给定的双循环交叉列表,对于第i个双循环交叉点的第j个移动,存在两个可能的交叉街道移动排队图,如图2所示(为简单起见省略了下标u和j),取决于第一次绿灯时间是否足够大可以让在第一子循环中排队的车辆全部通过。考虑到交叉街道上的恒定流量的假设,这种通过运动的每个背景周期的均匀延迟是曲线下面的面积的总和,并且使用等式(1)和(2)计算。
注意,(公式)定义为第一个子循环中的实际直行车队放行时间,它是所需队列放行时间(公式)和可用绿灯时间(公式)的最小值,如图2 a和b分别所示。
所有十字路口和十字路口的总和给出了在十字路口上通过统一延迟的总数。在SC控制(公式)下使用跨越街道的统一延迟总数,在十字路口上的标准化总平均通过延迟目标(公式) 在方程式(3)中表示。
带宽的定义与基本MAXBAND编程中使用的相同,并且在目标函数中也被标准化,如等式(4)所示。 带宽的归一化使用可能可用于绿带通过BWmax的方向最大绿灯时长(公式)的加权和,其通过使用等式(5)-(7)确定。
沿着主干道的UDC交叉口。 参数(公式)是UDC下的直行阶段的总绿灯时间,(公式)是没有UDC控制的直行绿灯时长。等式(7)确定(公式)表示UDC下的环中的总绿灯时长与绿色时长的比率被假定为与UDC下的直通运动的总绿色时长与SC下的放行绿色时长的比率相同。 从背景周期长度中扣除总损失时间,得出环中的总绿色时长。 总损失时间是原始损失时间加上由于在环中引入两个子阶段而导致的额外损失时间的总和(假设所有放行阶段的相位损失时间相同)。等式(7)还计算交叉街道的该参数,稍后将在约束部分中使用。
参数g是ja方向上主干道上绿带通过的最大可用绿灯时间。它被确定为SC交叉点的最小绿灯时间中的较小者和沿着主干道的UDC交叉口的最大可用绿色时间的最小值。参数g是UDC下的直通阶段的总绿色时间,g是没有UDC控制的直行绿灯时间。等式(7)确定g表示UDC下的环中的总绿灯时间与绿灯时间的比率被假定为与UDC下的直行运动的总绿色时间与SC下的通过绿色时间的比率相同。从背景周期长度中扣除总损失时间,得出环中的总绿灯时间。总损失时间是原始损失时间加上由于在环中引入两个子阶段而导致的额外损失时间的总和(假设所有通过阶段的相位损失时间相同)。等式(7)还计算交叉街道的该参数,稍后将在约束部分中使用。
当k是带宽的权重时,目标函数是归一化带宽和归一化总均匀延迟的相反的加权和,如等式(8)所示。
2.2.2. 子相位信号周期时长和同步的约束
此模型中引入的新约束主要用于确定2.2.2节中延迟目标中的子相位绿灯时长,并描述新的带宽几何形状,并允许在2.2.3节中选择绿波带通过的一个子绿灯相位。
目标函数涉及计算双循环交叉点处所有方法的全红时长。左转相位持续时间和左转弯模式都影响在双循环交叉点处通过运动的全红灯时长。左转模式取决于两个子循环中的哪一个包含受保护的LT阶段以及左转弯是否在该子循环中超前或滞后。 表1和等式(9 -13)显示了主干道穿过阶段的全红时长的确定。 通过运动计算跨街道的全红时长遵循相同的方法。
其中总过街相位时长R和左转相位绿灯时长L被确定为(公式)
将方程(9)和(10)中所示的全红时长代入目标函数可能会因为绝对函数而影响它的凸性。 这通过用等式(14)中所示的二进制变量a替换绝对函数来改进,这通过析取编程等效于等式(15)。
如等式(16)所示,两个子绿灯时长总和等于总绿灯时长(由等式(7)确定),并且每个子绿灯时长应当满足如等式(17)(18)中所示的最小绿灯时长要求。
在每个子循环中,主要街道上的双向服务(通过和左转运动)同时开始和结束,所以跨街服务也是如此。 对于第一个子绿灯相位阶段,方程(19)成立。 给定通过绿灯g的总比例确定的等式(10),所有其他同步和对背景周期长度的求和自动保持
2.2.3。 带宽几何的约束
两个成对SC交叉点的带宽几何形状与原始MAXBAND公式相同。 当涉及UDC方案时,带宽几何形状变得非常复杂,因为绿色带可以选择通过两个子绿色相位中的任何一个。 这使得带宽几何结构与传统的定时参数定义非常复杂。 该模型引入了标称红灯的概念。 标称红色是背景周期中的时间范围,可能的绿色波段选择不通过。 它等于背景周期长度减去绿色带通过的子绿灯相位时间。 图3示出了例如UDC交叉点i和SC交叉点i 1处的带宽几何形状
对于UDC交叉点,方程(20)和(21)分别确定出站和入站标称红灯。对于SC交叉点,标称红灯遵循通过运动通常定义的干道红灯时长的计算。
引入标称红灯的概念允许将UDC交叉点处的入站和出站红色中心偏移D的原始定义修改为从入交叉口标称红灯r1的中心到出交叉口标称红灯r2的最近中心的时间。 为了便于计算D,定义绿色波段的出交叉口(入交叉口)更多通过子绿灯相位在时间点t开始,并且两个时间点之间的差值为t1-t2(如果出交叉口协调绿灯启动则为正) 点是入交叉口协调绿灯起点的右侧)。 然后使用方程(22)确定Di
与原始问题中使用的混合整数线性规划相比,由于目标函数中存在二次分量的延迟估计,所得模型是混合整数二次规划(MIQP)问题。 优化过程遵循以下步骤。 如果可以预先获得UDC交叉点列表,则可以跳过Step2:
(1)运行MAXBAND模型,
全文共5904字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[2218]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


