颗粒形态参数对模型砂浆砂粒填充性能和流变性的影响外文翻译资料

 2022-01-07 22:31:52

英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

颗粒形态参数对模型砂浆砂粒填充性能和流变性的影响

H. Hafid a bG. Ovarlez b cF. Toussaint dP.H. Jezequel dN. Roussel

巴黎东部大学，纳维尔实验室，巴黎，法国

d Lafarge研究中心，圣昆汀·费拉维耶，法国

摘要

在本文中，我们在模型实验室中研究了悬浮屈服应力流体中的各种砂粒混合物的流变行为。我们使用图像分析，评估研究的砂粒的形态。然后，我们测量这些颗粒的填充性质，发现，作为第一近似，颗粒的整体形状（即纵横比）是主要的调控填充性能的形态参数。最终我们使用磁共振成像（MRI）来评估这些砂在水包油乳液中的悬浮液流变行为，并表明屈服应力和稠度在相同的临界体积分数上有所不同，随机致密堆积分数和颗粒的松散堆积分数似乎是完全相关的。最后，我们认为屈服应力的变化与由于颗粒形态的变化引起的粘度变化之间存在相关性。

关键词

新制混凝土、可使用性、总量、砂浆、屈服应力

1 .引言

在欧洲许多地方，用于生产混凝土的天然圆形骨料的可用性已成为一个关键问题，并导致碎石骨料的市场份额增加。与此同时，对拆除后混凝土破碎所获得的混凝土废弃物的环境关注表明，在新建混凝土中加入再生混凝土骨料（RCA）成为了建筑行业的一部分。这两种趋势表明，非球形的破碎颗粒会在新拌混凝土或砂浆中形成刚性夹杂物。

这种演变对这些材料的流变性质产生重大影响。从文献中可以预测，随着颗粒形状从球形开始发生进一步变化，一致性（即屈服应力和粘度）将增加[1]。然而，为了确保颗粒形状的一些目标要求，在聚集体的形态上确定一些限制值以允许生产混凝土或甚至改进现有的破碎技术，有必要更好地定量理解颗粒形态的影响，以此来关注新制砂浆或混凝土的流变特性。

因此，在本文中，我们研究了悬浮在实验室模拟的屈服应力流体中的各种真实砂粒混合物的流变行为。我们使用图像分析，定量评估研究的砂粒的形态。我们还测量它们的填充性能。我们最终使用磁共振成像（MRI）来评估这些砂在水包油乳液中的悬浮液的流变行为。然后，我们研究形态、颗粒堆积和流动行为之间的相关性。我们最后发现了屈服应力的变化与由于颗粒形态的差异引起的粘度变化之间存在相关性。该相关性允许通过简单测量屈服应力的变化来预计粘度的变化。

2 .材料和程序

2.1. 屈服应力流体模型

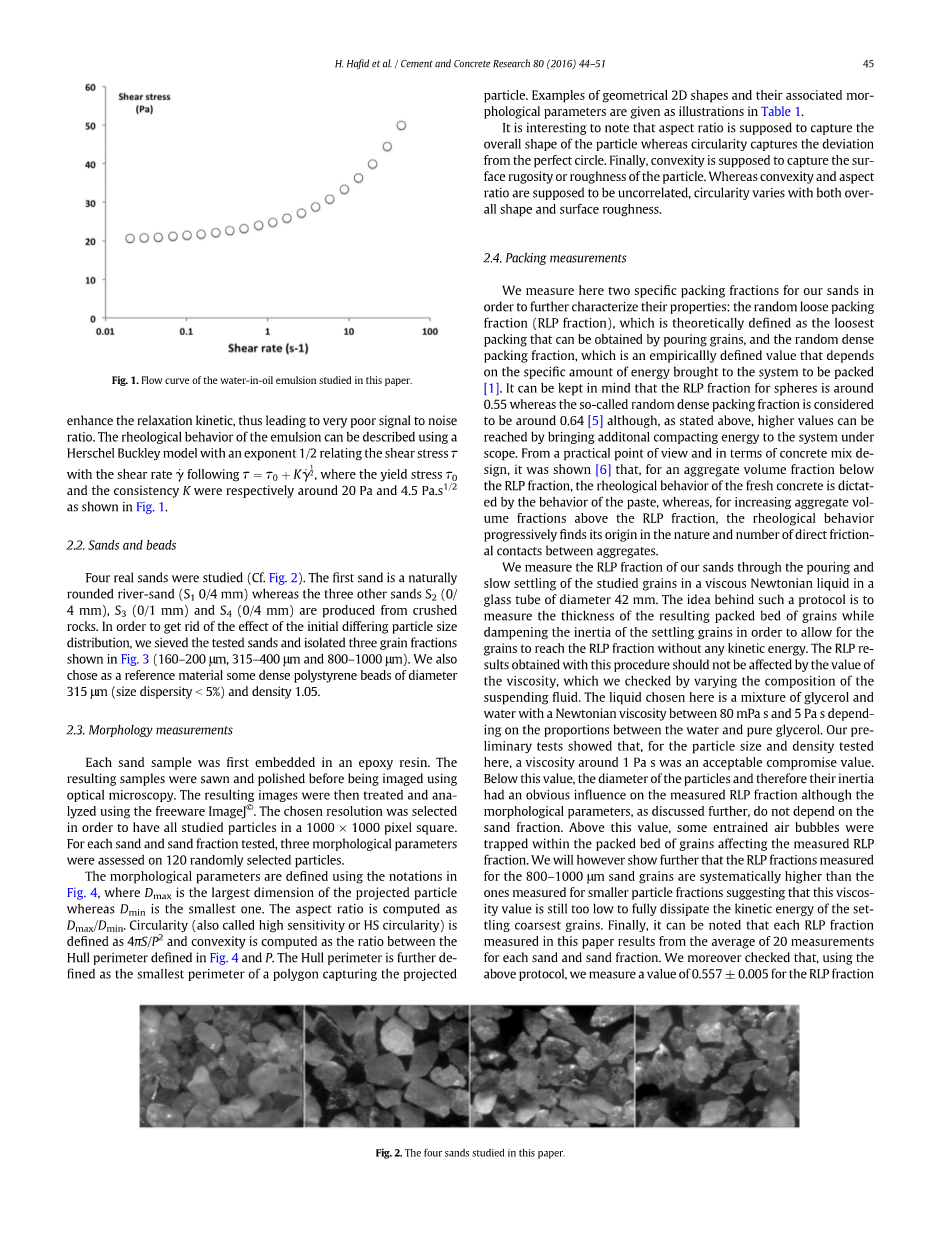
我们在这里研究悬浮在模型实验室中屈服应力流体中的真实砂粒混合物的流变行为。在[2]中详细研究了这些材料的行为，结果表明，单纯从流变学的观点来看，水泥浆中聚集体的悬浮液表现得像颗粒在任何其他屈服应力流体中悬浮的状态[3]。这就是为什么我们选择将颗粒悬浮在油包水乳液中，这种乳液已被证明是简单的屈服应力流体[4]。这种选择使我们能够避免与水泥浆流变学的不可逆和可逆演变相关的所有实验和分析复杂性，同时允许适当测量模型混凝土的流变性质随砂粒体积分数的变化[3] ]。此外，它大大简化了这项工作中进行的所有MRI测量，因为与水泥相比，这些系统不含Fe顺磁氧化物，这会增强弛豫动力学，从而导致非常低的信噪比。乳液的流变行为可用Herschel Buckley模型描述，剪切应力tau;与剪切速率的1/2次幂联系起来，其中，所述屈服应力tau;0和一致性K分别为约20 Pa和4.5 Pa·s1/2为所示图1。

图1 本文研究了油包水乳液的流动曲线。

2.2 . 砂和玻璃珠

我们研究了四个真实的砂（参见图2）。第一个砂是天然圆形河砂S1(0/4 mm)，而另外三个砂子S2(0/4mm)，S3(0/1mm)和S4(0/4mm)是由碎石制成。为了消除初始不同粒度分布的影响，我们筛选了测试的砂子并分离出图3中所示的三个颗粒级(160-200mu;m ，315-400mu;m和800-1000mu;m)。我们还选择了一些直径315mu;m （尺寸分散度 lt; 5％）和密度1.05的致密聚苯乙烯珠粒作为参考材料。

图2 本文研究了四种砂。

图3 砂粒和样品筛分的粒度分布。

2.3 .形态测量

首先将每个砂样品包埋在环氧树脂中。在使用光学显微镜之前，将所得样品锯切并抛光，然后使用免费软件ImageJ copy;处理和分析所得到的图像。选择该的分辨率是为了使所有研究的粒子都在1000times;1000 像素的正方形中。对于测试的每个砂子和砂子的部分，在120个随机选择的颗粒上评估三个形态学参数。

形态参数使用图4中的符号定义，其中Dmax是投影粒子的最大尺寸，而Dmin是最小尺寸。纵横比计算为Dmax / Dmin。圆度（也称为高灵敏度或HS圆度）定义为4pi;S/P2，凸度计算为图4中定义的船体周长与P之间的比率。周长进一步定义为捕获投影粒子的多边形的最小周长。2D几何形状及其相关形态参数的例子如表1中的说明给出。

图4.最小尺寸Dmin和最大尺寸Dmax及其周长的粒子（黑色阴影）,定义为捕获粒子的最小凸多边形的周长（灰色阴影）。粒子表面标记为S及其周长P。

表1. 2几何形状D及其形态参数的示例。灰色单元格中以粗体显示的值不依赖于此处选择的形状，并且对于此特定几何形状是恒定的。

有趣的是，纵横比应该确定粒子的整体形状，而圆形度确定其与完美圆的偏差。最后，凸起应该表示表面的粗糙度或颗粒的粗糙度。尽管凸度和纵横比应该是不相关的，但圆度随总体形状和表面粗糙度而变化。

2.4 .填充尺寸

为了进一步表征它们的性质，在这里我们测量砂的两个特定的填充分数：随机松散填充分数（RLP分数），理论上定义为可以通过浇注颗粒获得的最松散填料，以及随机密集填充分数，这是一个经验定义的值，取决于带给系统的特定能量数量[1]。可以记住，球体的RLP分数约为0.55，而所谓的随机密集填充分数被认为是约0.64 [5]，尽管如上所述，通过使附加的压缩能量达到更高的值来达到更高的RLP值。从实际的角度和混凝土混合设计的角度来看，它已被发现出来[6]：对于低于RLP分数的总体积分数，新拌混凝土的流变性质取决于糊状物的性质，而对于高于RLP分数的总体积分数，流变性质逐渐取决于聚集体之间直接摩擦接触的性质和数量。

我们通过在直径为42 毫米的玻璃管中的粘性牛顿液体中倾倒和缓慢沉降所研究的颗粒来测量我们的砂的RLP分数。这种方案背后的想法是测量所得颗粒填充床的厚度，同时抑制沉降颗粒的惯性，以使颗粒在没有任何动能的情况下达到RLP部分。通过该程序获得的RLP结果理论上不受粘度值的影响，我们通过改变悬浮液的组成来检查粘度值。这里选择的液体是甘油和水的混合物，它的牛顿粘度在 80mPa·s和 5Pa之间，具体取决于水和纯甘油之间的比例。我们的初步测试表明，对于此处测试的粒度和密度，约 1Pa·s 的粘度是可接受的折衷值。低于该值，颗粒的直径以及因此它们的惯性对测量的RLP分数具有明显的影响，尽管进一步讨论的形态参数不依赖于砂子比例分数。高于该值，一些夹带的气泡被捕获在填充的颗粒床内，影响测量的RLP分数。然而我们发现：由800-1000mu;m砂所测量的RLP值系统性地大于粒径较小的砂所测值，这表明，这个粘度值仍然太低，不足以完全消除沉降最粗颗粒的动能。最后，可以注意到，本文中测量的每个RLP分数来自每个砂子和砂子部分的20次测量的平均值。我们还检查了使用上述方案，我们测量球形单分散聚苯乙烯珠的RLP部分的值为0.557plusmn;0.005，这与文献[5]中报道的值相似。

我们测量 50mm容器中的随机密集填充分数，该容器经受 50Hz 振幅，振幅为0.5mm。在样品上方施加630g 质量，如图5所示。我们检查了在我们实验室中可用的频率，振幅和载荷方面的所有其他压实方法对随机密集填料部分给出了较低的值或导致一些砂粒的破碎。可以注意到，这里选择的程序与de Larrard [1]推荐的程序非常相似。

图5 使用外部载荷和振动进行随机密集填料分数测量。

最后，可以记住，对于在这项工作中进行的所有填充测量，使用[7]中提出的校正来计算壁效应。

2.5. 流变学测量

实验是在宽间隙Couette型流变仪中结合MRI进行的[8]，[9]，[10]，[11]。MRI用于测量几何间隙内材料的局部速度和浓度分布，而Bohlinreg;C-VOR 200流变仪用于平行测量扭矩，以获得完全相同的方案，几何形状和流动历史。内圆柱半径Ri为4.15cm，而外圆柱Re的半径为6 厘米。对于此处测试的最粗砂，因此间隙与颗粒尺寸之比约为18。两个圆筒用砂纸覆盖以防止任何滑动。实验方案旨在接近新混凝土流变学中使用的标准方案[12] ; 这些实验通常很短，应该有助于避免剪切引起的或重力引起的不均匀性[13]，[14]。通过实验，我们发现上述不均匀性确实可以忽略不计。然而，迁移始终存在于所研究的最高体积分数[14]，我们必须将其考虑在内（见下文）。增加的旋转速度从4转到100 转（每一步持续20 s）因此随后旋转速度从100转/分钟到5 转/分钟（参见图6）。对于每个旋转速度，使用MRI [11]，[14]，[15]，[16]测量间隙内的局部速度分布。用于从扭矩和MRI测量中检索所研究材料的流变学参数的程序在[11]，[14]，[15]，[16]中给出。

图6 实验方案和流程历史。每个步骤持续时间为20 秒。

体积分数曲线的测量对于评估可能的不均匀性至关重要，并将其考虑在内[11]，[14]。当单独使用宏观流变测定时，这种不均匀性确实显示出导致错误的测量[11]，[14]。在这种现象不可避免的最高体积分数下，这尤其显着。在下文中，我们以流变参数的形式直接呈现[14]中详述的分析结果，作为真实（局部测量的）体积分数的函数。

3 实验结果

3.1 形态参数

我们在图7中绘制了纵横比和凸度作为所测试的砂和砂子部分的圆形度的函数。可以注意到，凸度和圆度与这里研究的砂粒相关。因此，在下文中，我们将仅保持纵横比和凸度作为限定所研究的砂粒形状的独立参数。

图7 所有测试砂和球形聚苯乙烯珠的形态参数之间的相关性; （左）长宽比作为圆度的函数; （右）凸度作为圆度的函数。垂直条代表120个测量粒子的不确定性。绘制球形珠粒而没有不确定性用于视觉引导。

我们在图8中绘制了所有砂子和砂子部分的这两个参数。我们得出结论，在我们测量的不确定性中，这里测量的形态参数确实随砂型而变化而不是砂粒级。换句话说，无论研究的是什么部分，来自一个给定砂子的所有颗粒都具有相似的形状。必须记住，这个结果不能推广到整个粒度分布，因为可以预期砂子S2，S3和S4的破碎过程可能会在小颗粒部分产生较针状颗粒，而不是所研究的部分这里。以砂S1为参考，我们得出结论，所有其他砂岩都具有较高的纵横比和较低的凸度图2和图3中的S3和S3具有相似的纵横比但具有不同的凸度，并且S3和S4具有相似的凸度但具有不同的纵横比。砂S4显然是与圆形光滑形状最偏离的一个，因为它可以从图1中的图片明显地发现。

图8 各种砂和砂子部分的纵横比（左）和凸度（右）。图中还绘制了球形聚苯乙烯珠粒的值。

3.2 填充分数

我们在图9中绘制本文研究了各种砂和砂组分的随机致密堆积分数和RLP分数。可以注意到，此处针对球体获得的致密填充率（69％）高于64％的标准值。然而，它低于面心立方和/或六边形密堆积晶格可达到的74％最大值。该

全文共12070字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[1894]

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章