奥氏体不锈钢304L和316L在高温下的机械性能外文翻译资料

英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

奥氏体不锈钢304L和316L在高温下的机械性能

a 比拉理工学院机械工程系，彼拉尼，海得拉巴，印度

b Gokaraju Rangaraju工程技术学院机械工程系，海得拉巴，印度

摘要: 用于各种高温环境的奥氏体不锈钢304L和316L是非常重要的合金，这使得研究它们在高温下的机械性能变得非常重要。在本研究中的机械性能，比如极限拉伸强度（UTS），屈服强度（Y_s），伸长率（%），应变硬化指数（n）和强度系数（K）是根据单轴等温拉伸试验得到，实验温度范围是50～650℃，以50℃为间隔步长，并以三种不同的应变速率（0.0001,0.001和0.01sminus;1）进行高温拉伸试验。利用人工神经网络（ANN）来预测这些机械性能。调整好的人工神经网络模型给出了极好的相关系数，而且误差值也非常低，这代表了模型的良好精度。开发的人工神经网络模型的准确性也符合平均配对t检验，F检验和Levene检验的结果。

关键词: 奥氏体不锈钢；机械性能；拉伸试验；人工神经网络

1. 引言

奥氏体不锈钢（ASS）304L因其在海水环境中的优异耐腐蚀性而广泛应用于国防和核科学领域^[1]。 奥氏体不锈钢304L的这种性能是由于钼的存在，这可以防止氯化物的腐蚀。它还具有低含碳量，从而改善了磨损和摩擦性能并且降低了对晶间腐蚀的敏感性^[2]。 奥氏体不锈钢316L还在核科学领域得到了应用。它被用作快速增殖反应堆中的核燃料包覆管和燃料子组件包装材料的制造材料，因为其在高温下具有优异的机械性能和与液体钠的良好相容性^[3]。 因此，这些钢在核反应堆中特别有用。反应堆的温度通常很高。因此，研究材料在高温下的行为及其性能变得势在必行.

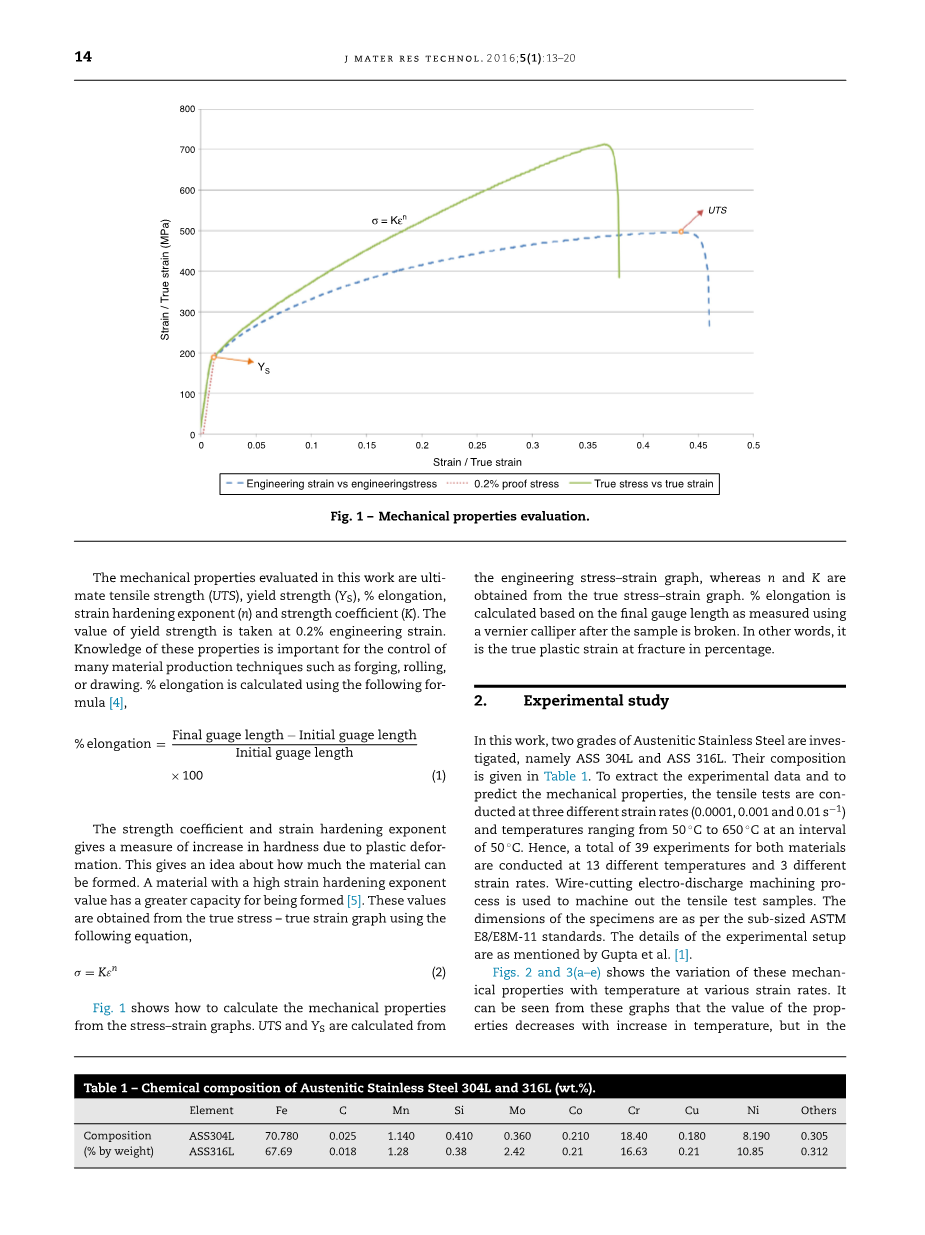
图1 机械性能评估

在这次实验中评估的机械性能是极限拉伸强度（UTS），屈服强度（Y_s），伸长率（%），应变硬化指数（n）和强度系数（K）。当工程应变为0.2%时，取得屈服强度值。了解这些特性对于许多材料生产技术（例如锻造，轧制或拉伸）的控制非常重要。使用下面的公式计算伸长率（%）^[4]。

(1)

强度系数和应变硬化指数给出了由塑性变形引起的硬度增加的量度。这给出了一个关于材料成型能力的概念，具有高应变硬化指数值的材料具有更强的成型能力^[5]。 这些数值是使用以下等式从真实应力 - 真实应变图中得到的。

（2）

图1展示了如何从应力 - 应变图中计算出力学性能。UTS和Y_s 的计算依据为工程应力 - 应变图，而n和K是从真实的应力 - 应变图获得的。在样品断裂后，使用游标卡尺测量的最终标距长度来计算伸长率（%）。换句话说，它是断裂时真正的塑性应变百分比。

1. 实验研究

在这次实验中，研究了两种规格的奥氏体不锈钢，即奥氏体不锈钢304L和奥氏体不锈钢316L。表格1给出了他们的成分。为了提取实验数据并预测机械性能，拉伸试验在三种不同的应变速率（0.0001,0.001和0.01sminus;1）下和50～650℃的温度范围内进行，间隔步长为50℃。也就是说，在13种不同的温度和3种不同的应变速率下，对这两种材料进行了总共39次实验。线切割电火花加工工艺用于加工拉伸试样。样品的尺寸符合ASTM E8/E8M-11标准。实验装置的细节如Gupta等人所述。

表1 奥氏体不锈钢304L和316L的化学组成 (wt%)

图2和3（a-e）表明了在不同的应变速率下这些机械性能随温度的变化而变化。从这些图中可以看出，这些性能的值随着温度的升高而降低，但是在温度范围为300-550℃时，未遵循此趋势。可以看出UTS持续降低直到温度为300℃，接下来UTS基本保持不变直至550℃。Y_s 和伸长率（%）也先急剧下降后趋于稳定然后再次下降。还发现K和n值在上述区域中先降低后增加，然后在600℃后又降低。这种性能的不规则变化是由于动态应变老化的影响（DSA现象，可能与Portevin-Le Chatelier效应有关）^[6,7]。

图2 奥氏体不锈钢304L的（a）UTS，（b）Y_s，（c）伸长率

（%），（d）n，（e）K在不同的应变速率下，相对于温度的变化

这些机械性能不遵循任何特定的趋势，这使得我们很难用任何一种方程来预测。人工神经网络（ANN）技术非常适合此目的。人工神经网络是一种人工智能技术，已被应用于描述许多过程，在这些过程中对物理机制的理解非常困难^[8,9]。 人工神经网络在数字软件或硬件中模仿生物神经系统的行为。这种方法不需要经过在算法上将输入转换为输出的明确定义的过程。人工神经网络的最大优点之一是它们使用任意函数近似机制，它从一组代表性数据中“学习”。然后，当训练样本作为输入时，人工神经网络进行自适应，并再现期望的输出。对于该模型，既不需要明确的数学理解，也不需要物理变化的物理知识。在人工神经网络的预测建模应用中，它充当加权输入的总和，以给出输出或预测值。与通过数学方程建模相比，使用人工神经网络技术可以更容易地估算出机械性能^[10]。

出的均方误差最小化。

反向传播网络的上述参数通常是通过反复试验和利用保留的测试数据评估泛化能力(或更复杂的交叉验证)来确定的。然而，还有另一种新的方法来寻找神经网络的最佳结构。该方法首先找出神经网络具有最小均方误差(MSE)的层数。这一层是神经网络的最优层，可以训练集。但是，在某些情况下，由于泛化上限的丢失，测试数据可能无法满足网络的要求。因此，使用正规化的机器学习技术，即减少网络的层数和减少网络的代数，发现对于奥氏体不锈钢304L来说最佳层为6，对于奥氏体不锈钢316L来说为17。如图4（a）所示，最小MSE发生时的层数为16，但是由于该网络不能满足测试数据的要求，因此采用了正则化的机器学习技术，选择了6层。图4（b）显示了奥氏体不锈钢316L的MSE与层数之间的关系。

图3 奥氏体不锈钢316L的（a）UTS，（b）Y_s，（c）伸长率（%），（d）n，（e）K在不同的应变速率下，相对于温度的变化

1. 人工神经网络模型的发展

神经网络体系结构包括层数的规范，每层中神经元的数量，每个神经元执行的激活函数的类型，以及神经元之间的可用连接。权重w的值被赋值给网络A中的连接，加权输入（x）然后被映射到y1（x，w，A），即输出的预测值。这些参数改变了有效性的学习模型，例如，隐藏神经元的数量，以及权重衰减项等。

在文献中，已经发现前馈反向传播神经网络正被人们用来训练出非常可靠的网络。反向传播学习算法使用梯度搜索技术来使网络输出的均方误差最小化。

反向传播网络的上述参数通常是通过反复试验和利用保留的测试数据评估泛化能力(或更复杂的交叉验证)来确定的。然而，还有另一种新的方法来寻找神经网络的最佳结构。该方法首先找出神经网络具有最小均方误差(MSE)的层数。这一层是神经网络的最优层，可以训练集。但是，在某些情况下，由于泛化上限的丢失，测试数据可能无法满足网络的要求。因此，使用正规化的机器学习技术，即减少网络的层数和减少网络的代数，发现对于奥氏体不锈钢304L来说最佳层为6，对于奥氏体不锈钢316L来说为17。如图4（a）所示，最小MSE发生时的层数为16，但是由于该网络不能满足测试数据的要求，因此采用了正则化的机器学习技术，选择了6层。图4（b）显示了奥氏体不锈钢316L的MSE与层数之间的关系。

图4 （a）奥氏体不锈钢304L和（b）奥氏体不锈钢316L的人

工神经网络架构

人工神经网络模型的输入参数为温度和应变率，输出参数为UTS、YS、伸长率（%）、n和K。首先将输入归一化，从0.05到0.95，使用下面的传递函数方程来有效地激活。

（3）

其中X_min和X_max分别是输入X的最小值和最大值，X_n是对应X的规范化数据。一旦找到了经过最佳训练的网络，所有转换后的数据都会使用以下公式返回其原始值。

（4）

实验数据随机分为两部分。选择85％的数据点作为训练人工神经网络的培训用数据并以剩余的15%作为测试数据，以便得到单层人工神经网络中各层的最佳组合。这种训练测试验证程序采用Hastie等人的方法。该网络是在MATLAB 2012a版本中实现的。用于得到反向传播神经网络(BPNN)的训练函数是Levenberg-Marquardt训练函数(trainlm)。

一个好的神经网络在训练数据集和测试数据集上都有很好的相关性。然而，选择最佳的网络体系结构是很困难的。这些训练集有很好的相关性。 但是当涉及到一些看不见的数据时，大多数网络要么过拟合，要么低于拟合数据。最佳神经网络是在测试数据上具有最大相关性的神经网络，是一种合理的神经网络。 训练数据相关性高。通过计算总数据集与预测值的相关性，进一步验证了这一点。神经网络结构的选择使用上述标准完成。因此，发现奥氏体不锈钢304 L和奥氏体不锈钢316 L的最佳网络分别为[2-6-5]和[2-17-5]。该体系结构适用于一个具有2个输入和5个输出的中间层。前面提到的奥氏体不锈钢304 L的架构意味着中间层有6个神经元，而数字2和5根据输入(2)和输出(5)固定。奥氏体不锈钢316L的架构意味着它在中间层有17个神经元。这种架构如图所示，图5（a）和（b）分别对应奥氏体不锈钢304L和奥氏体不锈钢316L。

图5 均方误差与神经网络层数之间的关系图

1. 奥氏体不锈钢304L和（b）奥氏体不锈钢316L

4. 结果和讨论

为了验证人工神经网络模型的预测，对三个统计参数(相关系数、平均绝对误差和标准误差)进行了比较。相关系数（R）是一种统计工具，提供有关实验值和预测值之间线性关系强度的信息。平均绝对误差(∆)是用来衡量预测值与实验值的接近程度的量。它们是用下列公式进行计算的，

其中y_exp 是实验值，y_p 是预测值，_exp 和_p 分别是y_exp 和y_p的平均值，N是正在考虑的数据点总数。标准差表示数值与平均值的偏差。仅用相关系数不足以验证预测结果。模型的预测可能偏向于更高或者更低的值。因此，还计算了预测值与实验值之间的平均绝对误差(AVG)及其标准误差。

表2 训练数据的统计参数（85%的数据）

<td

全文共6889字，剩余内容已隐藏，支付完成后下载完整资料</td

资料编号：[1837]

您可能感兴趣的文章

• 复杂热电材料外文翻译资料
• 以自蔓延高温烧结方法制备热电化合物以及燃烧合成的新标准外文翻译资料
• 氮掺杂分级多孔碳作为氧还原反应的高效电化学催化剂的研究外文翻译资料
• 孪晶诱导塑性高嫡合金的设计外文翻译资料
• 含铌先进Fe-Cr-Ni型奥氏体耐热钢富铜相的析出强化在超临界电厂的应用外文翻译资料
• 不同温度下直接能量沉积层状工具钢的弯曲强度外文翻译资料
• BiFeO3的光伏效应外文翻译资料
• 通过氢稳定的MgaPt研究核壳纳米结构Mg@Pt中快速“氢泵”的可视化外文翻译资料
• 一种铱核心环金属有机配体显著地提高了有机太阳能电池 的光伏性能外文翻译资料
• 钠离子电池的高性能阳极材料:三组分共组装法制备层次多孔碳外文翻译资料