英语原文共 15 页,剩余内容已隐藏,支付完成后下载完整资料
基于裂缝离散转动求和的一种计算变形方法
1970年,Bachmann6.9提出了一种计算钢筋混凝土受弯构件变形的方法,该变形计算是通过裂缝之间的微元体转动而不是通过截面的曲率来计算的。这种方法考虑了裂缝倾斜的影响和裂缝之间混凝土张力的加强效应。在分析中,该构件被分成“弯曲破坏构件”(如图6.23的梁,内力以弯矩为主,所以只产生垂直裂缝)和“剪切破坏构件”(如图6.24的梁,其中存在剪力和弯矩,产生的是斜裂缝)。
1. 产生弯曲破坏微元体区域的变形
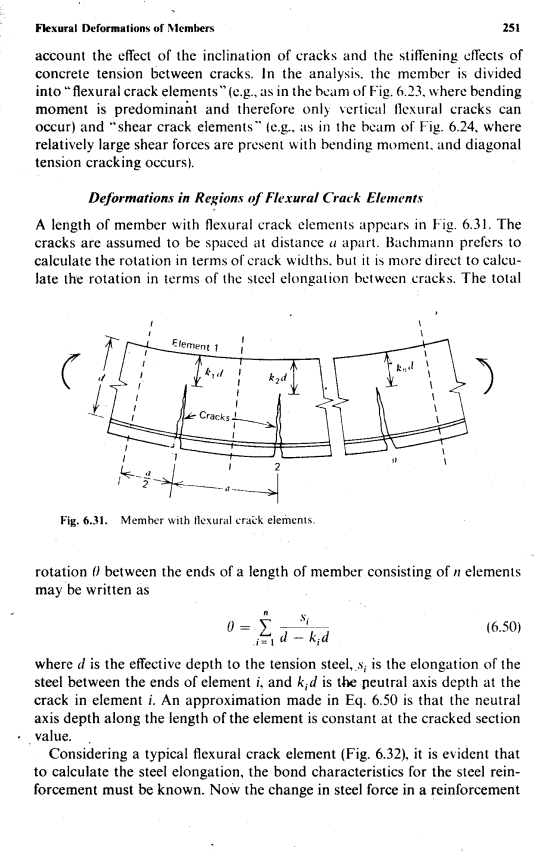
一段产生弯曲破坏构件如图1.1所示。假设裂缝间存在一定间距。Bachmann倾向于根据裂缝宽度计算旋转变形,但是根据裂缝之间的钢筋伸长率来计算旋转变形更直接。 由n个微元体组成的一段长度之间的总旋转角度theta;可以写为
(1.1)
其中是张力钢材腹板有效长度,是微元体的两端之间的钢材的伸长率,是元素中的裂缝处的中和轴的深度。公式1.1是元件长度方向的中和轴在裂纹截面的近似深度值,是恒定的。
图 1.1 产生弯曲破坏的构件
很明显,一个典型的弯曲破坏元件(图1.2),要计算钢材的伸长率,必须知道钢材的材料特性。现在,由于钢材应力的变化,在长度的钢筋中钢筋应力的变化由下式给出
(1.2)
其中粘结应力是距离裂缝中点的距离的函数。长度的钢的伸长率由下式给出
there4; (1.3)
其中是钢材应力的函数。
图 1.4(a)弯曲破坏元件;(b)粘结应力;(c)钢材应变分布;(d)钢材应力分布。
裂缝处和裂缝中间的钢材应力变化由方程1.4给出,为:
(1.4)
同样,两个裂缝之间的钢的伸长率根据方程式1.2和1.3求出,为:
(1.5)
裂缝处的钢应力可以使用常规裂缝截面理论从截面特性计算。然后,对于给定的裂缝间距,粘结应力分布和钢应力 - 应变曲线,裂缝之间的钢应力可以从公式1.2计算,并且两个裂缝之间的钢材伸长率可以从公式1.5计算。可以对所有弯曲破坏的元件进行相关计算。然后,通过这种方式确定的裂缝之间的钢伸长率和裂缝处的中性轴深度可以代入方程1.1,根据构件的长度给出旋转。
为了确定塑性铰的转动极限区域,必须要考虑产生塑性变形的所有的弯曲破坏的元件。Bachmann已经证明,只要裂缝间距,粘结应力分布还有钢应力 - 应变曲线已知,这种方法就可以很好地计算构件的塑性旋转。
2.发生剪切破坏区域的变形
在6.6.2节中,我们讨论了由倾斜的斜向拉伸裂缝引起的钢材应力增加。塑性铰区域中的对角线张力裂缝通过沿着构件展开屈服区域来增加可利用的塑性旋转。对于具有已知裂缝倾斜度和位置的给定对角线张力裂缝模式,裂缝处的钢材应力可以通过静力学使用平衡方程来计算,这个平衡方程考虑了由方程式7.32给出的剪切加固所承载的剪切的影响。这种纵向钢材应力的计算我们将在第7章中详细讨论。一旦确定了这些钢材应力,钢材的伸长率可以通过裂缝间距来计算。应力分布和钢应力-应变曲线,可以利用方程式6.53和6.54计算, 旋转角度可以通过公式1.1来计算。计算中最大的难点可能是假定的对角线张力裂缝的倾斜度还有位置。
前面的分析表明,最终旋转角度取决于塑性铰区域中存在的剪切力。在纯受弯区段,塑性旋转集中在相对较小的弯矩塑性铰处,并且所得到的塑性转动角可能不会很大。如果剪切应力足够高以至于引起对角线张力裂缝,那么剪切裂缝铰链将形成,塑性旋转能力增加,继而塑性变形发生在更宽的区域上。然而,显而易见的是,具有剪切变形的塑性铰区域的细部变形状态目前还不能通过分析来确定,未来需要在这个领域进行更多的研究分析。
6.7 在施加荷载的情况下构件的变形
6.7.1 弯矩和曲率的关系
大多数关于钢筋混凝土构件的弹性行为的已有研究成果都是从理论工作或试验中获得的,其中施加荷载也只是纯粹地调节为荷载最大值。很少有研究人员试图在标准的地震运动的高强度荷载下确定钢筋混凝土梁和柱截面的变化情况。在往复加载情况下对构件变化的理论研究的相关案例有Aoyama,6.15Agrawal, Tulin,和Gerstle, 6.16· Bertero 和 Bresler, 6.17Brown 和 Jirsa,6.18和 Park, 还有Kent和 Sampson。6.19这些理论中的大多数都是基于平截面假定的线性应变分布和钢筋混凝土的理想应力 - 应变曲线。通常通过计算相应的构件的极端纤维中的应变范围的力矩和曲率来得到构件的弯矩 - 曲率曲线。对于极端纤维中的给定应变,调整中性轴的深度,直到钢筋混凝土中的应力,根据材料的应变分布和应力 - 应变曲线确定并同时考虑之前的应变历史,以及作用在截面上的外力的力。然后计算对应于该应变分布的力矩和曲率。 Park,Kent和Sampson6.19使用的方法如下所示。
图 2.1循环加载下的钢材的应力 - 应变曲线证明了鲍辛格效应
以下是由Kent 还有 Park6. 20确定的关于中级钢的经验值的计算方法:
(2.1)
当施加的荷载次数为奇数时(n=1,3,5hellip;)
(2.2)
当施加的荷载次数为偶数时(n=2,4,6hellip;)
(2.3)
在这里是钢材应变,是加载运行开始时的钢材的应变,是钢材应力,是钢材的弹性模量,是之前加载过程中产生的钢材的塑性应变,n是施加荷载的次数(例如第一次应力翻转发生在n = 0,n = 1是第一次屈服应力反转,n = 2是第二次加载屈服后应力反转,等等)。假定通过在纵向钢周围布置紧密间隔的横向钢来防止被压缩钢材的弯曲。
循环荷载下混凝土的应力 - 应变曲线如图6.34所示。压缩应力的包络线ABCD可以用Kent和Park6.5确定的关系来表示由矩形箍限制的混凝土在由公式.2.6至2.11给出的单调荷载下的变化情况。测试数据显示(参见第2.1.1节),经历反复非弹性载荷的无侧限混凝土的包络线与单调曲线大致相同。 对于受约束的混凝土,假设具有相同的变化。可以假设混凝土的拉伸线性应力 - 应变曲线,其具有与零应力下的压缩曲线相同的斜率。 破裂模量的值可由方程2.2给出。
图 2.2 循环荷载下的混凝土的应力-应变曲线的变化
重复荷载下混凝土的性能如图6.34所示,可以假设图6.34的理想的变化情况。在从E点卸载时,假设先前应力的0.75在没有应变减小的情况下丢失,其中在斜率0.25Ec的线性路径上跟随到G点。如果混凝土没有破裂,则它能够承受拉应力。但如果混凝土先前已经破裂,或者在此加载阶段形成裂缝,则拉伸应变会增加,但不会产生拉应力。 在重新加载时,应变必须重新获得G处的值,然后才能再次维持压应力。 如果在卸载之前重新加载产生零压缩应力,则重新加载遵循其中一个路径。注意,E和G之间的假定曲线的平均斜率相当于应力 - 应变曲线的初始切线模量。人们认为循环的更复杂的理想化是没有根据的。
压缩后的覆盖混凝土(环箍外)的应力 - 应变曲线可以假设遵循应变小于0.004的受限核芯区混凝土的曲线。 应变大于0.004的覆盖混凝土可被认为已经剥落并且强度为零。 这是因为横向钢将导致核芯区和覆盖混凝土之间的薄弱平面,并且在高强度负荷的几次反转之后覆盖混凝土可能变得失去作用。
3.分析方法
在规定的曲率极限之间确定循环加载的钢筋混凝土截面的理论弯矩-曲率曲线最好使用数字计算机进行。混凝土压缩应力的复杂分布发生在加载循环期间。确定作用在截面上的内力的大小和位置的最方便的方法是对作用在截面的离散元件上的应力求和。在该方法中,该部分被分成多个水平元素,每个水平元素具有该水平的部分的宽度。图6.35显示了T形截面的排列。如果从顶部开始编号n个元素,则每个元素将具有深度h / n,其中h是该部分的总深度。顶部和底部钢分别位于元素ndrsquo;/ h和nd / h中。如果顶部纤维中的应变是并且中性轴深度是,则元素中的平均应变是
(3.1)
从假定的应力 - 应变曲线中可以看出混凝土中的应力和每个微元中的钢材应力,并将其视为与元素中的平均应变相对应的应力。根据应力和每个微元体中的混凝土和钢的面积,可以确定截面上的力。
图3.1 T形截面的离散微元体
可以使用迭代方法来计算弯矩曲率曲线上的点。顶部混凝土纤维中的应变按照固定量调整。 根据的每个值,估计中性轴深度,并且针对该应变分布计算元件中的应力。 然后计算作用在微元体上的力,并通过使用要求来验证力的平衡。
(3.1)
其中C和T分别是作用在元件上的压力和拉力,P是作用在垂直截面方向上的压力(梁的情况下为零)。如果不满足平衡方程3.1,那么估计的中性轴的位置是不正确的,必须调整直到达到力的平衡,满足平衡方程为止。达到平衡之后,根据和P的给定值计算来计算弯矩M和曲率ѱ。
离散元件技术具有适用于由于循环加载引起的复杂应力分布的优势,并且使由于剥落引起的面积减小的微元体力并记录已经破坏微元体成为一件简单的事情。但是该技术的缺点在于计算对应于给定应变的应力相对较慢,需要为每个元件存储记录沿应力 - 应变路径的进展的参数。
4.比较两种弯矩-曲率响应
刚刚讨论的理论方法已经通过实验来进行了检验,该结果是从周期性加载的双重钢筋混凝土梁中获得的,该混凝土梁具有4.94英寸(125毫米)宽,8英寸(203毫米)深的矩形横截面。横梁固定在每一端,形成一个6英尺(1.83米)的简支支撑跨度,并在中跨通过圆柱形桩静态加载。通过反转负载应用的方向来循环施加荷载,应用了非弹性范围的几个载荷循环。在靠近柱接头的梁的临界区域中,在2英寸(51mm)标距长度上测量顶部和底部强化的应变。使用()/()。从这些数据来计算实验曲率,其中和分别是顶部和底部钢材的应变(受拉应变为正,受压应变为负),和是顶部和底部钢之间的距离。图4.2和4.3比较了两个光束的实验和理论曲率-曲率曲线。梁24包含等钢和底钢(rho; = rho;rsquo;= 1.11%),梁27包含不一样的顶钢和底钢(rho; = 3.54%,rho;#39;= 1.14%),其中rho;等于底钢的面积/ bd,rho;#39;等于顶钢的面积/ bd的
全文共7087字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[1777]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


