
英语原文共 14 页,剩余内容已隐藏,支付完成后下载完整资料
研究报告
风激励下无源摩擦阻尼传动塔线路系统性能评估
陈波项晓李云鹏和钟万里
武汉理工大学道路桥梁与结构工程重点实验室,武汉市珞狮路122号邮箱219号,武汉430070
武汉理工大学交通学院,武汉430070
广东电网股份有限公司,广州510080
2014年8月30日接收;2014年10月1日合格
学术编辑:易婷华
版权所有@2015陈波等人。这是一份根据知识共享署名许可分发的开放获取文章,允许在任何媒体中不受限制的使用、分发和复制,前提是原始作品被正确引用。
本研究采用受风激励的摩擦阻尼器对输电塔线路系统进行振动控制和性能评估。首先构造了输电塔的三维有限元(FE)模型。为了动态分析,开发了传输塔的二维集总质量模型。通过考虑塔架与输电线路之间的动态相互作用,提出了被动摩擦阻尼器的力学模型。建立了与受风激励干扰的摩擦阻尼器相结合的输电塔线路系统运动方程。以实际输电塔线路系统为例,研究了所提出的控制方法的可行性和可靠性。进行了广泛的参数研究,以找到摩擦阻尼的最佳参数,并评估滑动轴向刚度和磁滞回线对控制性能的影响。对示例结构的研究表明,应用具有最佳参数的摩擦阻尼器可以显着减少传输线路系统的风致响应。
1.简介
架空输电塔线路系统是世界范围内广泛用于能源供应的典型电力基础设施。作为一种高层结构,输电塔线路系统由于阻尼小而易于受到强烈的风激励[1-3]。由于强风荷载导致的输电塔线路系统的过度振动可能引起与诸如构件破裂,构件弯曲和塔架坍塌之类的事件相关的结构损坏或故障。世界各地经常报告风荷载作用下塔的失效[4-6]。为了减轻输电塔线路系统的动态响应,在过去的二十年中已经进行了许多的理论,实验和现场测量研究[7-9]。用于性能评估和控制的当前方法和技术可以分为两大类。第一个是通过在接受强烈水平的风激励的同时增加结构刚度而开发的传统方法。另一种是通过安装镇定控制装置来防止结构故障的替代方法。
目前关于输电塔线路系统振动控制的研究主要集中在动态吸收器和消能阻尼器的应用上[10]。通常用于减轻高层结构的振动的典型装置是调谐质量阻尼器(TMD)。TMD的应用可以在一定程度上降低结构动态响应,而应该在需要占用结构空间的输电塔顶部安装几个附加质量块。此外,由于TMD的被动特性,它只能抑制调谐模式形状的振动而不是全局响应。因此,TMD对输电塔线路系统的控制性能有限。为了克服动态吸收器的缺点,最近开发了许多能量消散阻尼器作为动态缓解输电塔线路系统的替代方法。到目前为止,输电线路系统在动力响应作用下的振动控制很少被研究[11,12]。Chen等人提出了一种利用粘弹性阻尼器[13]对输电塔线路系统进行抗风设计的新方法。然而,据广泛报道,粘弹性阻尼器的性能仍在恶劣环境下可以大大减弱,这对于露天的输电塔线路系统是无法避免的[10,14]。诸如MR阻尼器的半主动控制装置的配置和制造非常复杂,并且在振动控制过程期间对额外能量供应的要求在接受强烈激励的同时是不现实的。因此,可采用结构简单,环境适应性强的被动摩擦阻尼器来抑制输电塔线路系统的风致响应,摩擦阻尼器是结构响应控制应用中使用的典型的能量消散装置,它可以制造成轴向构件来代替普通结构,而不需要额外的空间占用。
为此,本研究积极开展了受风荷载作用的无源摩擦阻尼传输塔线路系统的振动控制和性能评估。首先建立了输电塔的三维有限元模型,然后建立了相应的二维集总质量模型。通过考虑了铁塔与输电线路之间的动态相互作用,提出了输电塔线路系统的解析模型。通过考虑摩擦阻尼器轴向刚度的影响,给出了摩擦阻尼器的力学模型。建立了考虑风扰动的输电线路系统在平面内和平面外的运动方程。以我国南方实际建成的输电线路系统为例,验证了该控制方法的可行性和可靠性。此外,本文还进行了详细的参数化研究,以考察滑行力、轴向刚度和控制回路对控制精度的影响。观测结果表明,在阻尼器参数被确定的情况下,被动摩擦可以抑制输电塔线路系统的风振控制,因为它具有良好的能量消散能力。
2输电塔线路系统模型
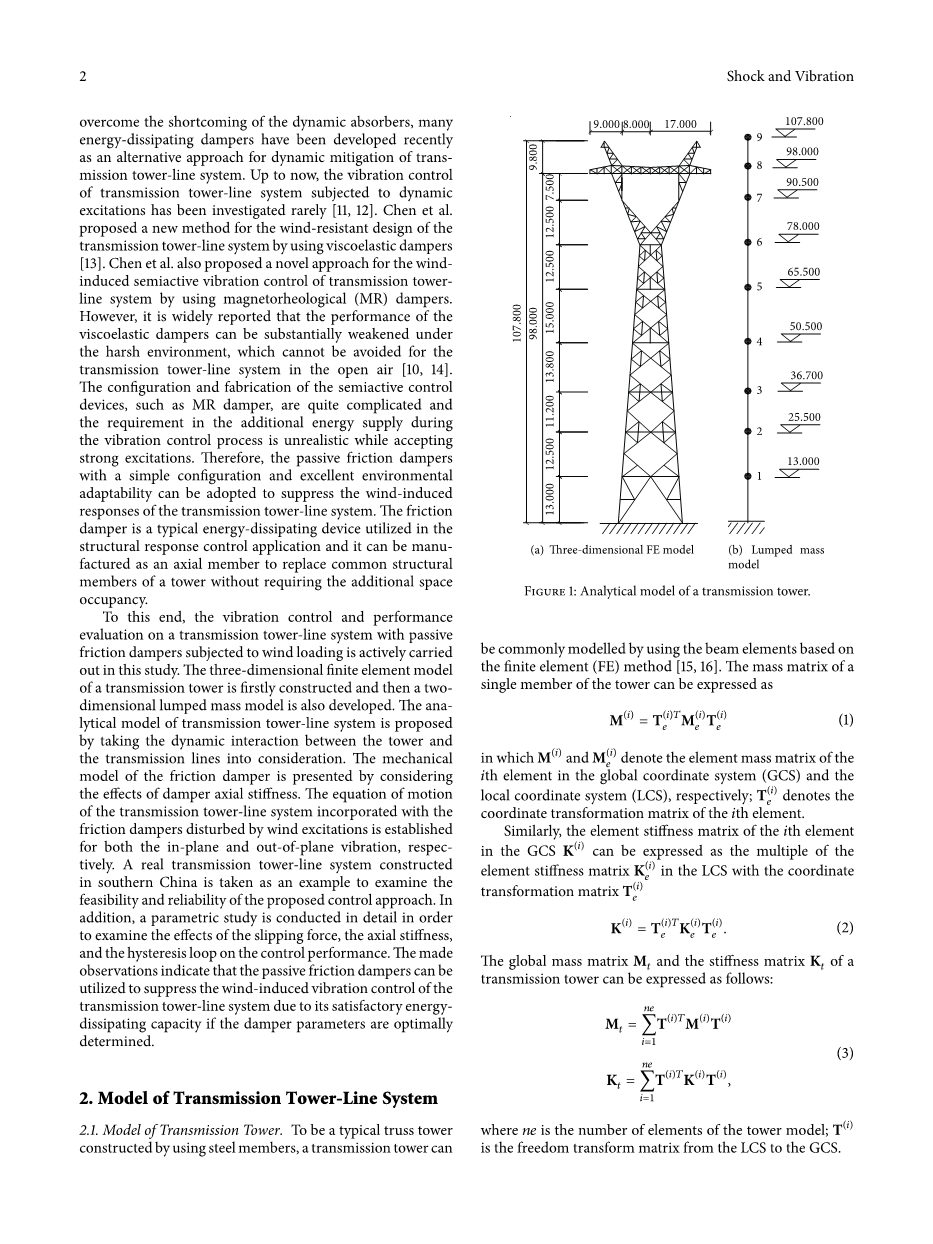
2.1输电塔模型。作为一种典型的用钢构件建造的桁输电塔通常可以采用基于有限
- 三维有限元模型 (b)集总质量模型
图一:输电塔的分析模型
元(FE)法[15,16]的梁单元建模。塔的单个构件的质量矩阵可以表示为
(1)
其中和分别表示全局坐标系(GCS)和局部坐标系(LCS)中第i个单元的单元质量矩阵,表示第i个单元的坐标变换矩阵。
同样,GCS中第i单元的单元刚度矩阵可以用坐标变换矩阵表示为LCS中单元刚度矩阵的倍数。
(2)
传递塔的整体质量矩阵和刚度矩阵可以表示如下
(3)
其中ne是塔模型的元素数;是从LCS到GCS的自由度变换矩阵
- 面内振动 (b)面外振动
图2:传输线的MDOF弹性模型
传输塔的三维(3D)FE模型如图1(a)所示。如果由于大量的结构构件和部件而使输电塔的结构非常复杂,则可以预期塔的自由度(DOFs)的显著数量。因此,对于动态响应计算和对控制性能的研究是不切实际的,因为时域中的数字逐步积分将非常耗时。此外,塔上的动态激励,例如风荷载,通常可以建模为时间上的静止或非平稳随机过程,并且在空间中是非均匀的。对传输塔的复杂三维有限元模型的动态加载的模拟需要大量的计算工作。从实际的角度来看,具有有限自由度的输电塔的简单分析模型对于结构动力响应和参数研究的研究更为合理。在这方面,二维(2D)集总质量模型通常在实践中用于检查复杂传输塔的动态响应。
当传输塔的3DFE动态模型简化为2D集总质量模型时,通常采用一些假设。就二维集总模型而言,输电塔的质量,包括所有结构部件的质量和所有非结构部件,首先仅集中在几个楼层。某一楼层上所有节点的平均位移定义为该楼层沿该方向的名义位移。然后,二维质量模型的动态自由度数是所选楼层的数目。二维质量模型的质量矩阵M可表示为
(4)
其中m表示第j层的质量;nm是传输塔的楼层数。通过采取以下步骤实现在输电塔三维有限元模型的基础上,可以得到其二维质量模型的刚度矩阵K。
- 在三维模型的第i层的每个节点施加相同的水平力,使所有力之和等于1。
- 确定每个节点在第j层的位移。定义第j层的名义位移,使其具有弹性系数(i,j=1,2,hellip;hellip;,nm)。
- 形成灵活性。 用矩阵Psi;和逆柔度矩阵求出输电塔的二维刚度矩阵K。
2.2.输电线路系统模型。传输线可以被建模成与许多弹性元件相连的多个平行质量[17,18]。 在图2中显示了平面内/平面外振动,有6个均匀质量和5个弹性单元。对于传输线的平面内振动的解析模型,用广义速度和广义位移分别计算输电线路的动能和势能。应用哈密顿变分原理可导出传输线的运动方程[19].传输线的动能可以用该公式来表示
(5)
其中和是传输线的广义坐标,它分别与角theta;和长度l的差有关;和是传输线中第i个质量在水平方向和垂直方向上的位移。
同样,传输线的势能由下列公式确定
(6)
其中E和A是传输线的杨氏模量和截面面积,是第j单元的长度,是变形后的第j单元的长度。通过计算动能对广义速度的偏微分,可以确定质量矩阵M。同样,可以通过计算势能对广义位移的偏微分来确定刚度矩阵K。
图2(B)显示了传输线对平面外振动的解析模型。该传输线可作为一条具有多个质量的悬挂线。而传输线的质量矩阵和刚度矩阵可以表示为
(7)
给出了塔线路系统在平面内振动时的动能计算公式。
(8)
其中nl和nt分别是输电线路系统的传输线数和塔数。同样,给出了塔线路系统的势能计算公式。
(9)
通过将(8)和(9)代入回归方程,通过计算动能T和势能U与坐标及其第一次导数的偏微分得到输电线路系统平面内振动的质量矩阵M和刚度矩阵K。同样,考虑传输线引起的耦合效应,也可以确定输电塔线路系统平面外振动的质量矩阵M和刚度矩阵K[1]。
3.摩擦阻尼器模型
被动摩擦是利用固体摩擦机理实现能量耗散的装置。在实际中,这一概念已被机械工程师成功地应用于控制机器和汽车的运动。被动摩擦阻尼器可以在特定的外部激励(图6)下以特定的最佳滑移力。摩擦阻尼装置的发展始于20世纪80年代初,此后在结构振动控制中研制了大量的新型减振装置[20-23]。
图3:被动摩擦阻尼器的结构。
图4:摩擦阻尼器的力学模型。
一种典型的被动摩擦阻尼器的结构如图3所示。在早期阶段,摩擦力阻尼器的控制力表示为摩擦力N和摩擦系数的乘积,而不考虑阻尼器轴向刚度K的影响。然而,摩擦阻尼器的性能与阻尼器的轴向刚度密切相关。在试验研究的基础上,建立了多种弹性轴向构件的力学模型。
通常,摩擦阻尼器的控制力通过弹性轴向构件传递给结构。因此,摩擦阻尼器的模型应该包括弹性构件的刚度,如图4所示。在图4中,S表示第i摩擦阻尼器的滑动力,它等于摩擦力N与摩擦系数的乘积;e第i摩擦阻尼器的滑移变形,初始值为零;E表示阻尼器的杨氏模量;A是第i个弹性构件的截面面积,L是第i个构件的长度。第i个摩擦阻尼器的控制力可表示为
(10)
其中k表示被动摩擦阻尼器的轴向刚度。
被动摩擦阻尼器的夹紧力是预先设定的,其摩擦力在滑动过程中是恒定的。第i个被动摩擦阻尼器的状态及控制力使用下列规则确定。
图5:被动阻尼器的受力流程图。
- 如果摩擦阻尼器没有滑动,则
(11)
- 如果摩擦阻尼器有滑动
(10)
其中d和分别是第i个摩擦阻尼器两端的相对位移和速度。当第i个摩擦阻尼器两端的相对位移增量d大于零时,控制力为拉力。否则,控制力是压缩的。
(3)当控制力u为相对位移增量d的不同符号时,摩擦阻尼器处于支杆阶段。在这种情况下,摩擦阻尼器的阻力和滑动应确定如下(11)。
图5显示了用于判断摩擦阻尼器的滑动情况和控制力的流程图。
4.输电线路系统的运动方程
通过假设风激励是一个平稳的随机过程,可以借助频谱表示法来模拟作用在输电塔线系统上的风载荷。随机风激励可以通过以下公式来建模[24]
(13)
其中N是足够大的数;是频率增量;是上限截止频率,条件是当gt;时,交叉谱密度矩阵的值很小;代表一系列独立的随机相位角,均匀分布在间隔[ 0,2 ]上;是矩阵的一个典型元素,由的Cholesky分解定义;是的复角。
图6:摩擦阻尼器的安装方案
表1:摩擦阻尼器的参数
杨氏模量(N/m) 截面面积(M2) 最大滑移率(M)
2.06 times; 10 7.5 times; 10 0.08
输电线路系统在风荷载作用下平面内振动的运动方程如下
(14)
其中,,分别是平面内振动的位移、速度和加速度响应;,,分别是用于平面内振动的塔线系统的质量矩阵、阻尼矩阵和刚度矩阵;是平面内的风荷载向量矩阵。同样,平面外振动的运动方程也可以表示为
(15)
(15)中符号的含义类似于(14)中的符号。
含摩擦阻尼器的输电塔线系统在平面内和平面外振动时的运动方程可表示如下:
(16)
其中和分别是平面内振动和平面外振动的摩擦阻尼器的控制力;和是平面内振动和平面外振动的摩擦阻尼器控制力影响矩阵。
5.案例研究
为了验证所提出的基于摩擦力的控制方法的可行性,本文以我国实际建立的输电线路系统为例,对其控制性能进行了研究。该塔的高度为107.8米,输电线路的跨度为400米,如图1所示。输电线路轴向刚度Ea为4.8times;107N,每米重量为1.394times;107N。在有限元方法的基础上建立了三维模
全文共8091字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[700]
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


