
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
热电方钴矿CoSb3的脆性破坏机理
材料合成与处理先进技术国家重点实验室(武汉理工大学)中国湖北武汉 430070
材料科学系 西北大学伊利诺斯州埃文斯顿60208
材料与加工模拟中心 加州理工大学 加利福尼亚州帕萨迪纳 91127
摘要:基于CoSb3的方钴矿有较高的热电效率,但是较低的断裂强度是商业应用中需要考虑的问题。我们利用密度泛函理论研究沿着各种剪切和拉伸变形下的响应去了解CoSb3脆性来源。我们发现Co-Sb键主导着理想强度。在所有的剪切和拉伸变形路径中,沿着(001)/lt;100gt;滑移系剪切具有最低理想强度,表明这是在压力作用下最有可能被激活的滑移系。我们也发现,由于Sb-Sb共价键比Co-Sb键更柔软,Sb环刚度比Co-Sb框架小,这导致Sb环在Co-Sb框架之前软化。进一步的变形会导致解构Sb环和Co-Sb框架的坍塌,导致结构失效。此外,我们发现,用如Na,Ba或Yb典型填料填充CoSb3空隙空间对理想强度和模型失效几乎没有影响,这可以被理解为他们对Sb环影响很小。
- 引言
热电(TE)发电装置已经在为太空飞船的深空任务提供动力等应用上发挥重要作用。现在,因为它们可以直接将热量转换成具有高可靠性且没有活动部件的电能,所以它们被考虑用于汽车废热气的回收。高效的热电能转换对于推进热电的应用是必要的。基于CoSb3的n型填充方钴矿被认为是最有前途的TE材料之一,因为它具有优异的TE品质因数(zTgt;1),但CoSb3的工程应用具有挑战性。例如,CoSb3 TE材料和金属接头之间的热膨胀差异很容易导致显著的热机械应力,导致接近CoSb3和接合金属之间界面出现裂缝,因此,机械强度和韧性对于方钴矿CoSb3材料的工程应用至关重要。
由于其对工程应用的重要性,最近已经研究了CoSb3的机械性能。Rogl和Rogl报道了掺杂方钴矿CoSb3的实验力学性能,如弹性模量,断裂韧性和破坏应力,他们表明CoSb3的机械性能与其他TE材料相比具有竞争性;Ravi等人专注于描述先进方钴矿材料的弹性模量,弯曲强度和断裂韧性;Ruan等人研究基于CoSb3的方钴矿化合物在压缩-压缩疲劳中的低循环应力控制疲劳性能;Schmidt等人报道了随温度而变的p型Ce0.9Fe3.5Co0.5Sb12和n型Co0.95Pd0.05Te0.05Sb3方钴矿热电材料的杨氏模量,剪切模量和泊松比,发现杨氏模量和剪切模量随温度线性下降。Yang等人使用分子动力学模拟(力场)来检查CoSb3的应力-应变关系,发现它是一种典型的脆性材料;Li等人利用分子动力学研究纳米多孔方钴矿CoSb3热电材料的拉伸/压缩力学行为,发现单晶CoSb3的弹性模量随孔隙率的增加而降低。然而,脆性破坏的机理和CoSb3的内在力学性能仍然未知。
为了确定CoSb3中脆性断裂的机理,我们在Perdew-Burke-Ernzerhof(PBE)功能水平上使用密度泛函理论(DFT)来预测单晶CoSb3的拉伸和剪切变形特性。在这里,我们沿着各种晶格取向变形,直到无法揭示原子尺度上的内在失效机制,我们发现CoSb3的最低理想强度是(001)/lang;100rang;滑移系,这是因为与其他变形系相比,这个变形系导致Co-Sb键的拉伸最小。由于Sb-Sb共价键比Co-Sb键软,Sb环的刚性弱于Co-Sb骨架,导致Sb环在Co-Sb骨架之前软化,进一步的外部变形表明,Sb环的解构和Co-Sb骨架的坍塌导致结构失效。为了检查填充对力学的影响,我们将Na,Ba和Yb原子加入CoSb3的内在孔隙中,但未发现CoSb3的理想强度和失效模式有明显影响。
2.方法
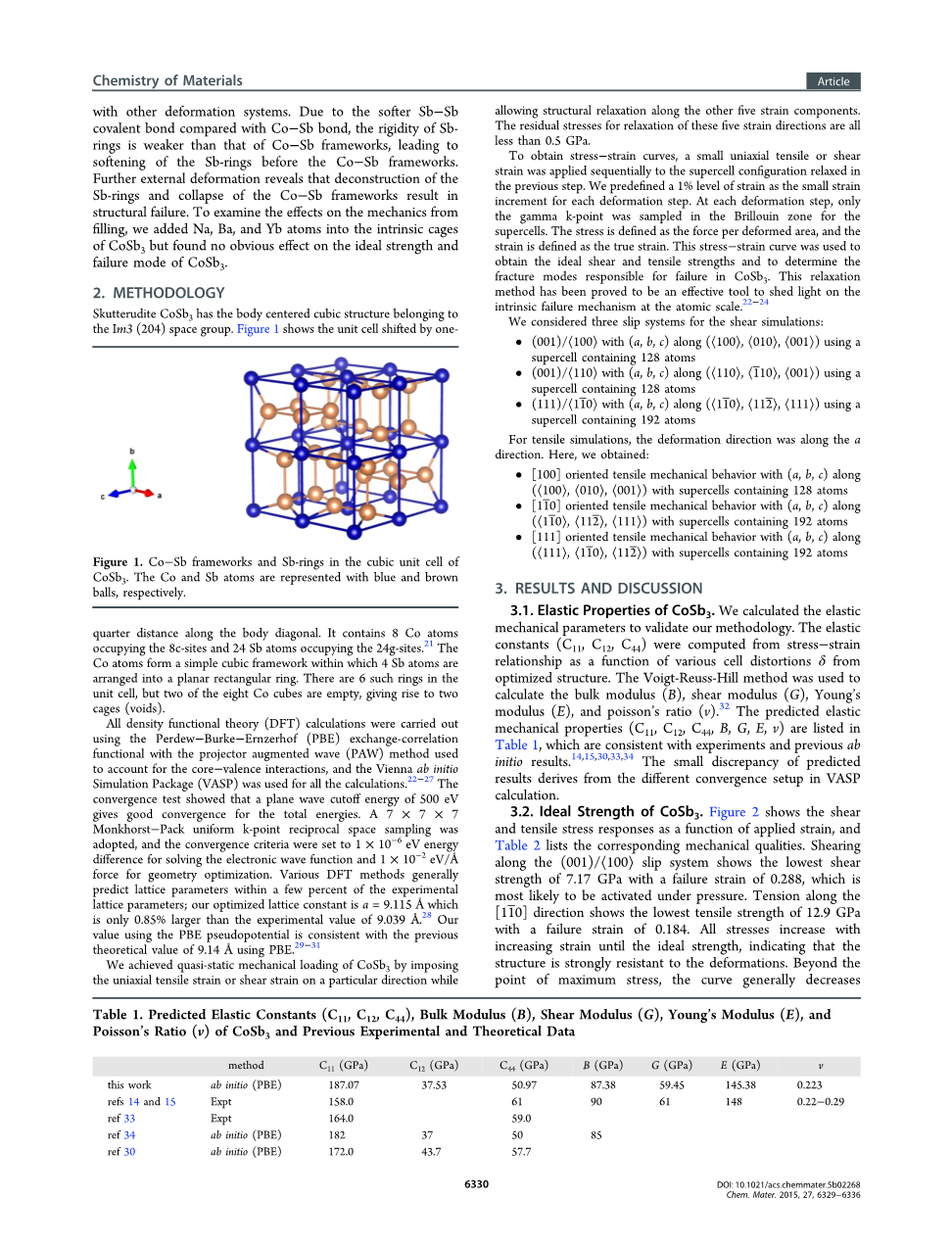
方钴矿CoSb3具有属于Im3(204)空间群的体心立方结构。图1显示了沿着体对角线移动了四分之一距离的晶胞。
图1:CoSb3的立方晶胞中的Co-Sb框架和Sb环,Co和Sb原子分别用蓝色和棕色球表示
它包含占据8c位点的8个Co原子和占据24g位点的24个Sb原子,Co原子形成简单的立方体框架,其中4个Sb原子排列成平面矩形环。单元格中有6个这样的环,但是8个Co立方体中有两个是空的,产生了两个网箱(空洞)。
使用Perdew-Burke-Ernzerhof(PBE)交换相关函数和用于解释核-价相互作用的投影增强波(PAW)方法进行所有密度泛函理论(DFT)计算,Vienna ab initio Simulation Package(VASP)用于所有计算。收敛性测试表明,500eV的平面波截止能量为总能量提供了良好的收敛性,采用7times;7times;7Monkhorst-Pack统一k点倒易空间采样,收敛准则设定为1times;10-6eV能量差,用于求解电子波函数和1times;10-2eV/Aring;力用于几何优化。各种DFT方法通常预测实验晶格参数的百分之几内的晶格参数,我们优化的晶格常数a=9.115Aring;,仅比实验值9.039Aring;大0.85%,我们使用PBE赝势的值与使用PBE的先前理论值9.14Aring;一致。
我们通过在特定方向上施加单轴拉伸应变或剪切应变同时允许沿着其他五个应变分量的结构松弛来实现CoSb3的准静态机械载荷,这五个应变方向的弛豫残余应力均小于0.5GPa。
为了获得应力-应变曲线,将小的单轴拉伸或剪切应变顺序地施加到在前一步骤中松弛的超单元构造。我们预定1%的应变水平作为每个变形步骤的小应变增量,在每个变形步骤中,仅在Brillouin区域中对超单元采样伽马k点。应力定义为每个变形区域的力,应变定义为真应变,该应力-应变曲线用于获得理想的剪切和拉伸强度,并确定导致CoSb3失效的断裂模式,这种松弛方法已被证明是一种有效的工具,可以揭示原子尺度上的内在失效机理。
我们考虑了剪切模拟的三个滑移系统:
- (001)/lang;100rang;与(a,b,c)沿(lang;100rang;,lang;010rang;,lang;001rang;)使用含有128个原子的超晶格。
- (001)/lang;110rang;与(a,b,c)沿(lang;110rang;,lang;10rang;,lang;001rang;)使用
超晶胞含有128个原子
- (111)/lang;10rang;与(a,b,c)沿(lang;10rang;,lang;11rang;,lang;111rang;)使用
超晶胞含有192个原子
对于拉伸模拟,变形方向沿着a方向,在这里,我们获得了:
- [100]取向拉伸力学行为,(a,b,c)沿(lang;100rang;,lang;010rang;,lang;001rang;)与含有128个原子的超级单体
- [11̅0]取向拉伸力学行为,(a,b,c)沿(lang;10rang;,lang;11rang;,lang;111rang;)与超级单元包含192个原子
- [111]取向拉伸力学行为,(a,b,c)沿(lang;111rang;,lang;10rang;,lang;11rang;)与含有192个原子的超级单元
3. 结果与讨论
3.1. CoSb3的弹性性质 我们计算了弹性力学参数以验证我们的方法,弹性常数(C11,C12,C44)由应力-应变关系计算,作为优化结构的各种单元失真delta;的函数,Voigt-Reuss-Hill方法用于计算体积模量(B),剪切模量(G),杨氏模量(E)和泊松比(v),预测的弹性力学性能(C11,C12,C44,B,G,E,v)列于表1中,这与实验和先前的从头算的结果一致,预测结果的小差异源于VASP计算中的不同收敛设置。
3.2. CoSb3的理想强度 图2显示了作为施加应变函数的剪切和拉伸应力响应,表2列出了相应的力学性能,沿(001)/lang;100rang;滑移系统剪切显示最低剪切
强度为7.17GPa,失效应变为0.288,最有可能在压力下活化,沿[10]方向的张力显示最低拉伸强度为12.9GPa,失效应变为0.184。所有应力随着应变的增加而增加,直到理想强度,表明该结构对变形具有很强的抵抗力。超过最大应力点,曲线通常单调减小,表明系统中的键软化,这对应于“屈服”过程。然后,在某一时刻,应力突然下降,表明软化键不再能够抵抗外部变形,导致粘合失效和结构坍塌。
表1. CoSb3的预测弹性常数(C11,C12,C44),体积模量(B),剪切模量(G),杨氏模量(E)和泊松比(v)以及先前的实验和理论数据
|
方法 |
C11(GPa) |
C12(GPa) |
C44(GPa) |
B(GPa) |
G(GPa) |
E(GPa) |
v |
|
|
实验 |
PBE |
187.07 |
37.53 |
50.97 |
87.38 |
59.45 |
145.38 |
0.223 |
|
参考文献14和15 |
Expt |
158.0 |
61 |
90 |
61 |
148 |
0.22minus;0.29 |
|
|
参考文献33 |
Expt |
164.0 |
59.0 |
|||||
|
参考文献34 |
PBE |
182 |
37 |
50 |
85 |
|||
|
参考文献30 |
PBE |
172.0 |
43.7 |
57.7 |
图 2.计算CoSb3在(a)剪切和(b)拉伸载荷的不同方向上的应力-应变。
表2.剪切和拉伸载荷下的理想强度和断裂应变
|
剪力 |
拉伸 |
|||||
|
力 |
(001)/lang;100rang; |
(001)/lang;110rang; |
(111)/lang;10rang; |
[100] |
[10] |
[111] |
|
理想强度(GPa) |
7.17 |
7.54 |
9.64 |
15.0 |
12.9 |
14.1 |
|
破坏应变 |
0.288 |
0.358 |
0.346 |
0.232 |
0.184 |
0.242 |
图3. 计算的原子位置与电子局域函数(ELF)的等值面结合,用于沿(100)/lang;001rang;滑移系统的剪切载荷:(a)应变0对应于初始阶段,(b)应变0.221对应于理想强度,(c)应变0.277对应于失效应变,(d)失效应变为0
全文共19466字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[350],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


