
英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
基于两相随机介质和有限元的岩土边坡稳定性分析
Yong Liu a, Huawen Xiao b,*, Kai Yao b, Jun Hu c, Hong Wei c
a武汉大学工程风险与防灾研究所水利水电工程科学国家重点实验室,中国武汉430072
b新加坡国立大学土木与环境工程系,新加坡117576号,1号工程大道2
c海南大学土木工程与建筑学院,中国海南省海口市美兰区人民路58号,海南大学,邮编570228
文章信息
文章历史:
收到日期:2017年5月31日
以修订后的形式收到:2017年8月4日
接受日期:2017年10月4日
在线提供,2017年10月31日
关键词:
边坡稳定性
数值计算
统计分析
有限元建模
随机场
蒙特卡罗模拟
摘要
为了研究岩土几何界面的强随机性,将岩土边坡视为两相随机介质。利用高斯场的非线性平移来模拟两相随机介质,从而可以检测土壤(或岩石)体积分数和土层倾角。采用随机介质作为材料性质的有限元方法确定岩土边坡的安全系数。蒙特卡罗模拟用于估计安全系数的统计特性。通过对边坡破坏初期最大主塑性应变的观测,研究了岩土边坡的破坏模式。结果表明,岩土边坡的临界面是相当不规则的,与纯土边坡的临界面有明显的不同。安全系数对土壤体积分布敏感,但可预测。利用岩土强度的加权调和平均值可以很好地预测安全系数,该预测模型实用、简单。对土层倾角的参数研究表明,当坡度角与土层倾角一致时,最不稳定的是土壤层。
2017年,中国地质大学(北京)和北京大学。由Elsevier B.V.制作和主持,这是CC BY-NC-ND许可证下的开放访问文章(http://creativecommons.org/许可证/由NC ND/4.0/)
- 介绍
岩土地质条件(图1)通常以随机布局的土层和岩层为特征,在岩土工程应用中广泛遇到((Ni et al., 1996; Toth et al.,2013; Qi et al., 2016; Tang and Xu, 2016))。Zhang等的一项调查研究。(2012)显示,在2008年汶川(中国)地震期间发生的334次滑坡中,35%为岩土边坡,表明岩土边坡普遍存在,应特别注意此类边坡的潜在危害和风险。然而,尽管开发了多种边坡稳定性分析方法(如Tang等人,2013、2015;Li等人,2015;Liu和Shields,2017;Liu等人,2018;Qi和Li,2018),但很少考虑岩土边坡稳定性。
岩土混合物的总体材料性质取决于岩土的布局和体积分数,因此,材料性质与均质和连续材料有很大不同(West和Hencher,1991年)。在这方面,两相随机介质的概念可能适用于模拟岩土混合物。“随机介质”一词是指土壤和岩石之间几何面上不连续性的强随机性。
高斯场的非线性转换可用于模拟两相随机介质(例如Griffiths等人,2012年;Feng等人,2014年;Shields等人,2016年)。在该方法的框架中,首先生成零均值和单位方差高斯随机场,然后将其转换为非高斯随机场。非线性变换可以保证目标的边缘非高斯概率,但它引入了自相关函数的一些变化。提出了各种方法来解决这些变化(Bocchini和Deodatis,2008;Shields和Deodatis,2013;Liu等人,2016,2017a),前提是已知非高斯场的特定自相关函数。
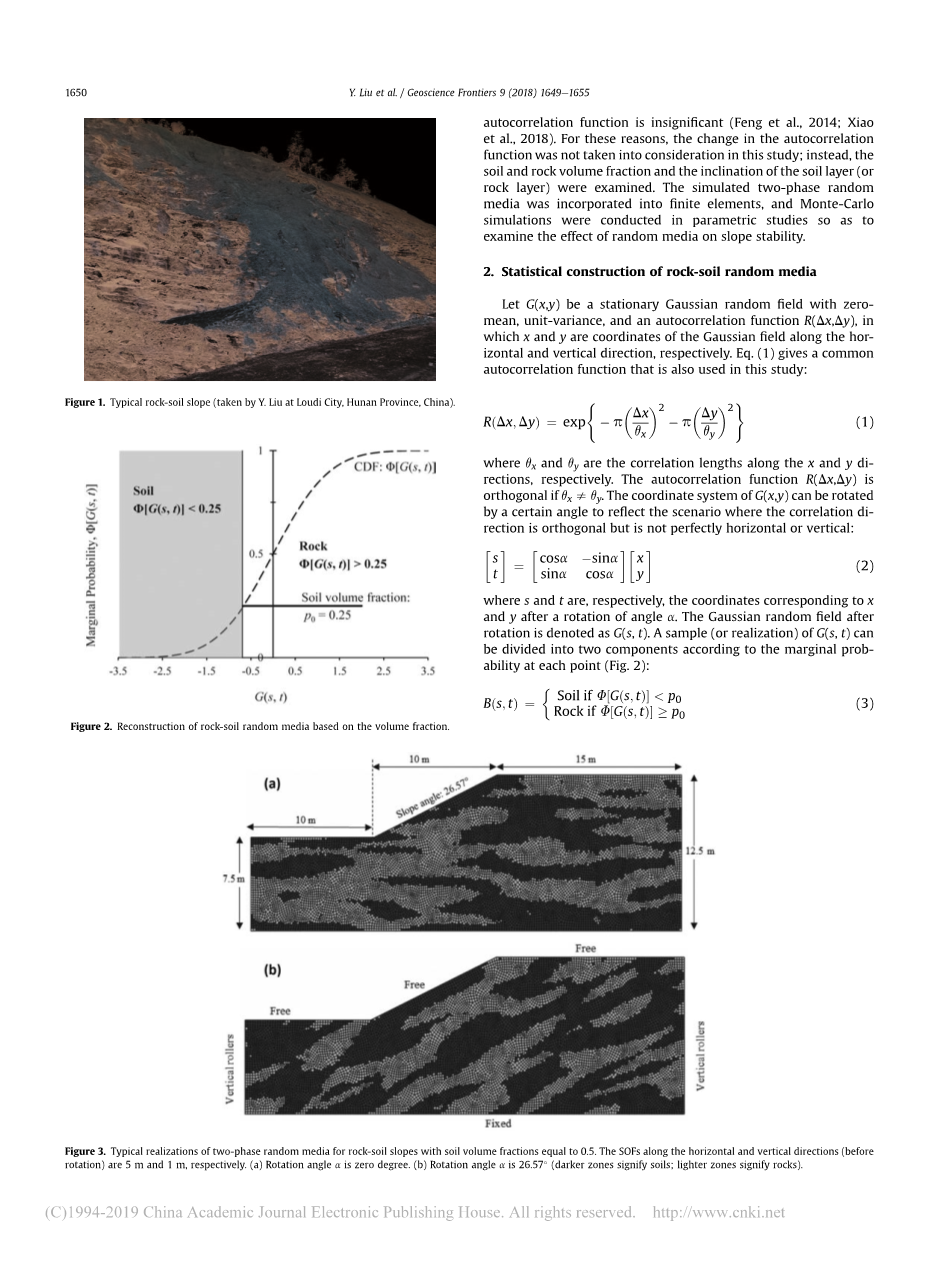
对于岩土混合物,不太可能根据有限的现场数据(通常是这样)以高精度估计自相关函数。然而,岩土混合料应具有自相关函数,该函数始终为正。在这种情况下,非线性翻译对自相关函数的影响是显著的(Feng等人,2014;Xiao等人,2018)。由于这些原因,本研究并未考虑自相关函数的变化,而是检查了土壤和岩石体积分数以及土层(或岩层)的倾斜度。将模拟的两相随机介质引入有限元中,并进行蒙特卡罗模拟参数化研究,以检验随机介质对边坡稳定性的影响。
图1.典型岩土边坡(湖南省娄底市刘勇摄)
- 岩土随机介质统计施工
设G(x,y)为平稳高斯随机场,具有零均值、单位方差和自相关函数r(dx,dy),其中x和y分别是沿水平方向和垂直方向的高斯场坐标。式(1)给出了本研究中也使用的一个共同的自相关函数: (1)
其中,和分别是沿x和y方向的相关长度。如果,自相关函数R(dx,dy)是正交的。G(x,y)的坐标系可旋转一定角度,以重新反映相关方向为正交但不完全水平或垂直的情况:
(2)
式中,s和t分别是a角旋转后x和y对应的坐标。旋转后的高斯随机场表示为G(s,t)。G(s,t)的样本(或实现)可根据每个点的边际可探测性分为两部分(图2):
(3)
图2,基于体积分数的岩土随机介质重建
图3.土体积分数为0.5的岩土边坡两相随机介质的典型实现。水平方向和垂直方向(旋转前)的SOFs分别为5 m和1 m。(a)旋转角度a为零度。(b)旋转角度a为26.57(深色区域表示土壤;较亮的区域表示岩石)。
表1
土壤性质参数及有限元模型
|
参数 |
符号 |
数值 |
|
摩擦角 |
|
0 |
|
土体不排水抗剪强度(kpa) |
|
10 |
|
扩张角 |
|
0 |
|
杨氏模量(kpa) |
|
|
|
泊松比 |
|
0.49 |
|
单位重量 |
|
18.0 |
|
边坡高度(m) |
H |
5 |
图4.有限元模型验证和二分法图解(fs=安全系数)
其中为土壤体积分数;B(s, t)为岩土随机介质;为累积分布函数。图2说明了式(3)的方法,利用改进的线性估计方法(刘等人, 2014)生成高斯随机场,得到式(3)中B(s, t)的两种典型实现,如图3所示。需要注意的是,式(2)本质上是一个雅可比矩阵,它引入了坐标系之间的旋转。在自相关函数中也经常引入等价性。然而,式(1)中的平方指数自相关函数不会受到这种限制,因为它的数学形式没有方向性。
表2 随机有限元分析结果总结
|
样本编号 |
土壤体积分数,P |
相关长度,m |
土的不排水抗剪强度,kpa |
岩石不排水抗剪强度,kpa |
岩土强度比 |
S方向与水平方向夹角 |
蒙特卡罗模拟的安全系数 |
||
|
沿S方向 |
沿t方向 沿T方向 |
平均值 |
变异系数 |
||||||
|
1 |
0.5 |
5 |
1 |
10 |
50 |
5 |
0 |
1.10 |
0.13 |
|
2 |
0.0 |
5 |
1 |
10 |
50 |
5 |
0 |
3.17 |
0 |
|
3 |
0.15 |
5 |
1 |
10 |
50 |
5 |
0 |
2.23 |
0.10 |
|
4 |
0.3 |
5 |
1 |
10 |
50 |
5 |
0 |
1.63 |
0.13 |
|
5 |
0.7 |
5 |
1 |
10 |
50 |
5 |
0 |
0.80 |
0.09 |
|
6 |
0.85 |
5 |
1 |
10 |
50 |
5 |
0 |
0.68 |
0.05 |
|
7 |
1.0 |
5 |
1 |
10 |
50 |
5 |
0 |
0.63 |
0 |
|
8 |
0.5 |
5 |
1 |
10 |
30 |
3 |
0 |
0.93 |
0.08 |
|
9 |
0.5 |
5 |
1 |
10 |
100 |
10 |
0 |
1.40 |
0.21 |
|
10 |
0.5 |
5 |
1 |
10 |
50 |
5 |
15° |
1.12 |
0.13 |
|
11 |
0.5 |
5 |
1 |
10 |
50 |
5 |
26.57° |
1.08 |
0.12 |
|
12 |
0.5 |
5 |
1 |
10 |
50 |
5 |
45° |
1.08 <!--全文共6153字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[451562],资料为PDF文档或Word文档,PDF文档可免费转换为Word |
|
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


