
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
岩体的扰动对岩石边坡采用霍克–布朗破坏准则的稳定性的影响
A.J. Li; R.S. Merifield; A.V. Lyamin;
迪肯大学工程学院,维多利亚州3217,澳大利亚
纽卡斯尔大学土木工程与材料模拟中心,NSW 2308,澳大利亚
摘要
在岩石中形成人工或“切割”斜坡的过程总是导致岩体内部的应力释放,进而引起一定程度的破裂和扰动。当采用爆破技术形成边坡时,扰动的程度尤其显著。然而,这种扰动对整个岩质边坡稳定性的影响在目前的文献中还没有得到彻底的调查。为了考虑到岩体施工过程中的干扰,干扰因素已被列入霍克–布朗准则[ 1 ]。本文采用有限元上限和下限的限制分析估计基于霍克–布朗准则准则同时包括岩体扰动的影响岩质边坡稳定性。进行了一组严格的分析,其中扰动的水平被认为是恒定的或线性变化的整个斜坡。然后将结果与一些报告的案例历史进行比较,以供核查之用。研究结果表明,扰动因子对岩质边坡稳定性评价有重要影响,特别是对质量较差的岩体。因此,在估计干扰程度时,必须谨慎地进行工程判断。此外,利用稳定的图表,不考虑岩体的扰动可能会导致显著高估估计挖方岩石边坡的稳定性。
关键词:安全系数; 极限分析; 稳定性数字;非均匀;
1.介绍
由于岩体的变化性质通常包含关节,断层,自然发生的不连续性和各向异性,因此估计岩石边坡的稳定性常常变得困难。由于其实际重要性,这一经典问题在文献[2-4]中引起了广泛的关注,其中已经证明Mohr-Coulomb准则不足以描述岩体强度。针对这个缺点,Hoek和Brown [5]和Hoek等人[1]提出了一种非线性破坏准则,广泛用于估算岩石或岩体的强度。 Marinos等人最近讨论了这一标准的适用性和局限性。 [6]这里不再重复。
一般来说,为了评估边坡稳定性,极限平衡法是最广泛使用的。然而,大多数基于极限平衡法(LEM)的商业软件需要传统的摩尔 - 库仑土参数,内聚力(c)和摩擦角(phi;)作为输入。大多数计算机程序需要莫尔 - 库仑土参数作为输入,因此完全忽略了岩体破坏包络线的非线性特性。非线性在边坡稳定性问题[7]中可用的低围压下更为明显。因此,应用非线性标准(如Hoek和Brown提出的标准)是克服常规Mohr-Coulomb标准等线性标准缺点的必要条件。霍克和布朗[8]和霍克等人。 [1]提供了一种方法,可用于将岩体强度参数转换为等效的Mohr-Coulomb参数。然而,这种转换被发现对极限承载力[9]和斜坡稳定性安全系数[10]产生了不一致的估计。发现使用等效参数和原生屈服准则之间的差异达到了承载能力的157%和边坡稳定性的64%。这表明处理岩石和岩石问题的最好方法是直接在计算中使用Hoek-Brown破坏准则。
在Hoek等人 [1],Hoek-Brown屈服准则的最新版本表示为:
从方程(2) - (4)可以看出,mb,s和alpha;全部取决于5-100之间的地质强度指数(GSI)。由于比尼亚夫斯基的不同地质条件,GSI被引入来估计不同地质条件下的岩体强度发现岩体评级RMR系统[11]和Q系统[12]不适用于较差的岩体。参数D是表示干扰程度的因子。它的范围从原状岩体的原状为0到扰动岩体的性质为1。
目前的研究旨在调查干扰因素(D)对岩石边坡稳定性评估的影响。方程式中的其余参数(2) - (4)将不在这里讨论。在Hoek和Brown [8],Hoek [13],Wyllie和Mah [14]以及Marinos等人中可以找到关于如何估计Hoek-Brown强度参数(sigma;ci,GSI和mi)的更多细节。 [6]。
2.以前的研究
文献综述表明,使用Hoek-Brown强度参数(sigma;ci,GSI和mi)已经进行了非常少的数值分析。其主要原因是极少数商业软件包在其制定中包含Hoek-Brown标准。 Hoek-Brown破坏准则的等效或切向强度参数(ct和phi;t)经常与上限分析方法结合使用。这些解决方案可以在柯林斯等人的作品中看到。 [15],杨等人。 [16],杨和邹[17]和杨[18]。在这些研究中,假定扰动因子(D)为0,并且获得斜坡的优化高度。此外,单独使用上限方法,解决方案的真实范围无法包含在内。 Lyamin和Sloan [19,20]和Krabbenhoft等人开发的强大的数值上下限技术。 [21]是Hoek-Brown屈服准则可以直接用于模拟的理想工具。这些边界方法也可以在小范围内支持真正的解,并且已经被Merifield等人应用于承载能力和边坡稳定性问题。 [9]和李等人。 [10,22]。应该指出的是,Li等人的所有岩石坡度分析已经通过利用D = 0来执行[10,22]。
来自Hoek等人。 [1],D = 0的假设意味着岩石斜坡内的岩体不受干扰,如自然斜坡。 Hoek等人[1]也强调,对于小规模的岩石边坡爆破,D = 0.7和D = 1.0分别适用于良好的爆破和差的爆破,因为应力消除会导致一些干扰。另外,对于特大型露天矿,建议采用D = 1.0,因为大量生产爆破造成的重大干扰以及去除覆盖层带来的压力减轻。此外,对于使用机械挖掘的特大型露天矿,建议D = 0.7。根据Hoek等人的上述建议, [1],可以注意到将岩体扰动程度纳入估算人造填方和岩石切坡稳定性的重要性。
到目前为止,作者并没有意识到任何研究都集中在调查不同干扰因素幅度对岩石边坡稳定性的影响。因此,本文的目的是应用Lyamin和Sloan [19,20]和Krabbenhoft等人开发的有限元极限分析方法。 [21]研究岩体扰动对岩质边坡稳定性评价的影响。这部分研究假定斜坡的岩体是均质的。
除了对均质岩石边坡的研究之外,在第二部分研究中还考虑了斜坡中各种干扰因素分布对边坡估算的影响。关于扰动因子的利用变化及其幅度将在第4节中描述。
3.稳定性数字
由于泰勒[23]提出了一套稳定性图表,因此许多研究人员已经注意到边坡稳定性的图表解决方案[3,24-27]。关于岩石边坡稳定性评估,Hoek和Bray [3]提出的图表可以用于岩石和堆石坡。此外,Siad [27]的图表解决方案适用于估算裂隙岩石边坡的稳定性。然而,这两套设计图基于摩尔 - 库仑破坏准则,其要求内聚力和摩擦角(c和phi;)作为输入。此外,Zanbak [28]提出的设计图只适用于斜坡的倾倒问题。
由于图表解决方案对于实践工程师的重要性和便利性,Li等人[10,22]利用上下限定理生成了几组适用于Hoek-Brown强度参数(sigma;ciGSI,mi)的静力和地震岩石边坡稳定性的稳定图。在他们的研究中,稳定性数被定义为以下等式:
其中sigma;ci是完整的单轴抗压强度,gamma;是单位重量,H和F分别是坡度的高度和安全系数。本文也采用这种形式的稳定性数字来显示岩石边坡稳定性的计算估计值作为图解。应该强调的是方程式中的安全系数。 (5)用sigma;ci/gamma;H表示,因为这三个参数可以比Hoek-Brown屈服准则中的其他参数更容易和准确地测量。事实上,Hoek-Brown破坏准则之后的岩体边坡稳定性问题是相对于sigma;ci/gamma;H归一化的,因为由Hoek-Brown屈服准则预测的强度相对于sigma;ci是完全可缩放的。这可以通过Hoek的公式证明[13]。尽管方程(5)与传统的极限平衡分析不同,可以直接比较安全因素,正如Li等人所指出的那样。 [10,22]。
4.问题定义
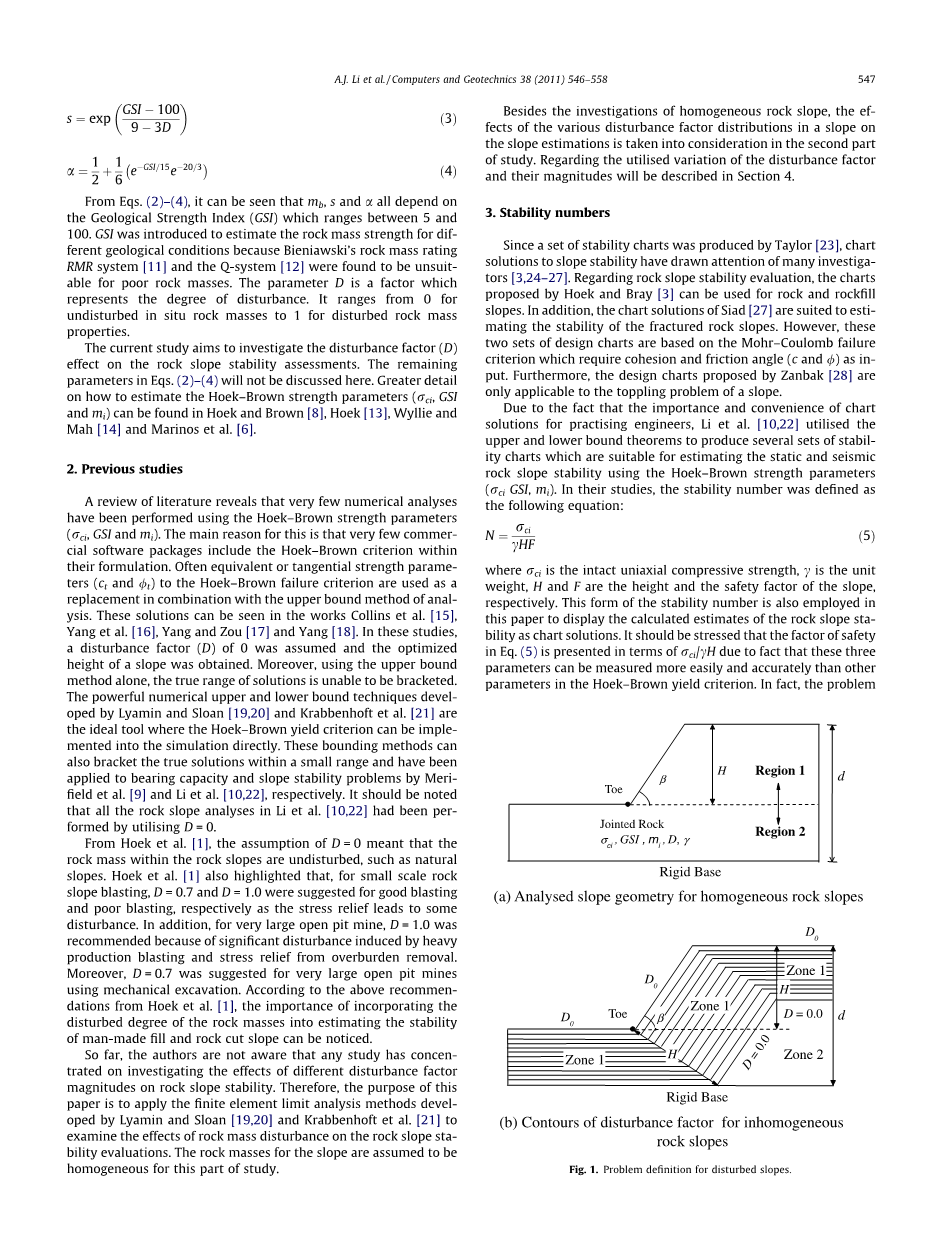
如图1a所示,本文分析的斜坡几何形状为均质岩石斜坡,其中节理岩体具有Hoek-Brown强度参数(sigma;ci,GSI,mi),D为0.7或1.0以模拟扰动水平在切割的岩石坡上。在极限分析中,对于给定的斜坡几何形状(H和beta;)和岩体强度,获得单位重量(gamma;)的优化解。在本文中,分析了一系列倾斜角度(beta;= 15°,30°,45°,60°和75°)。
所提出结果的适用性是由执业工程师确定并将取决于所讨论的斜坡的实际或可感知的扰动水平。例如,Tsiambaos和Saroglou [33]强调用GSI50挖掘岩体不需要爆破,因此这种扰动不是问题。但是,对于GSI50以上的非常大的斜坡或高应力环境,即使未采用爆破,由于应力消除造成的干扰水平实际上可能很大。
正如Marinos等人所指出的那样。 [6],模拟扰动因子的分布是合适的,随着离表面距离的增加而减小。 Cheng和Liu [29]以前的研究发现爆破伤害的主要影响区围绕挖掘周界深度约2 m。但是,Marinos等人[6]也表明,对于涉及许多吨炸药的非常大的露天矿山边坡,在开挖的斜坡后面观察到高达100米或更多的爆炸破坏。这些影响区域的扰动可以被看到显着变化,并且与受控爆破的质量和去除覆盖层的规模高度相关。 Hoek和Karzulovic [30]根据他们的经验推荐了潜在的受损区域范围。此外,干扰因子的初始大小也被提出并且可以在Hoek等人中找到。 [1]。
为了研究斜坡中各种干扰因素对稳定性数值的影响,本研究采用简单的扰动因子变化,随着深度的增加线性减小。在图1b中,主要受损区域(Zone 1)的形状基于Hoek和Karzulovic [30]确定,而参数D0是一个输入变量。另外,假定扰动岩体的范围从斜坡倾斜表面延伸1 H的深度。超过1 H(2区)范围的岩体被视为未受干扰,因此扰动因子D为零。鉴于上述假设,扰动因子的轮廓将平行于坡面。因此,斜坡的岩体是不均匀的。
应该指出的是,本文没有意图定义或量化确切的影响区和切割坡度的真实干扰分布。这部分研究的目的是通过比较稳定性数字来检查和理解各种干扰因素对岩石边坡稳定性的影响。为了获得更精确的岩石边坡稳定性估计,正如Marinos等人所建议的那样。 [6],需要将岩体划分为多个区域,并根据距离人脸的距离将D值递减到连续区域。为了比较干扰和未受干扰的岩质边坡的稳定性,方程(5)被采纳。
除了使用Lyamin和Sloan [19,20]和Krabbenhoft等人的极限分析制剂外, [21],商业极限平衡软件SLIDE [31]和Bishop的简化方法[32]也被用来与严格的极限分析解决方案进行比较。 SLIDE是基于LEM的商业软件,可以在其中分配广义Hoek-Brown失效标准。在分析中选择Hoek-Brown时,SLIDE将自动并瞬时计算出每个切片的一组等效Mohr-Coulomb参数。这些给定的凝聚力(c)和摩擦角(phi;)由每个单个切片底部的法向应力决定,可以代表与tau;-sigma;n平面内Hoek-Brown破坏准则的自然曲线相似的剪切强度。更详细的描述可以在Hoek [13]中找到。
5.均匀扰动的岩石边坡的结果和讨论
5.1。稳定性数字
图图2和图3分别给出了两组由D = 0.7和D = 1.0扰动因子的数值上下界方法获得的岩石边坡稳定性图。在图2a中,可以看出,公式(2)中定义的真实稳定性数(N) (5)受GSI = 10时上下极限分析解的限制。应该注意的是,边界法在所有分析中都将真正的稳定性数值置于plusmn;8%或更好的范围内。因此,为了简化,本文采用稳定性数字的平均值。参照图1〜如图2和图3所示,当GSI或mi减小时,发现稳定性数量N增加。在Li等人的研究中观察到类似的趋势。 [10]对于D = 0.0的情况。图1和2所示的三角符号。代表从极限平衡分析(SLIDE)获得的稳定性数字的2和3非常接近结合溶液的平均线。平均极限分析解与极限平衡分析之间稳定性数值的差异小于8%。
图1和图2显示了一系列倾斜角度(beta;= 15°,45°,75°)的不同扰动因子之间稳定性数值的比较。 其中D = 0.0的病例来自Li等人。[10]。 随着扰动因子对于给定的sigma;ci,GSI和mi增加,发现稳定性数目增加。 这一趋势表明,干扰程度较小(D)的岩体具有较高的安全系数,这是可以预料的。
参照图1〜如图4-6所示,发现在D = 0.0和D = 1.0之间稳定性数字的差异随着GSI的减少而增加。例如,在图6中,对于D = 0.0和mi = 5的情况,与D = 1.0相比,GSI = 90时的稳定性数字的比例约为1.33,而GSI = 10时的稳定性数字的比率为25.16。 D = 0.7时,D = 0.0至D = 0.7的稳定性数值比在1.18和6.78之间。这意味着,对于beta;= 75°的斜率倾斜,使用无干扰图表解(D = 0.0)来估计D = 0.7的扰动岩石边坡的稳定性将产生较大的不安全因子。如果忽略干扰因素影响,岩石边坡的安全系数将被高估,并且会得到一个不可靠的解。显然,仔细确定干扰因素值是必要的,因为它可能导致稳定性评估的显着差异。
看图。如图4-6所示,可以观察到对于各种倾斜角,GSI = 10和D = 0.0的稳定性数字可以大于或等于GSI = 50和D = 1.0的稳定性数字。为了确定这种现象的来源,已经观察到了Hoek-Brown破坏准则的本地形式和来自下限分析的滑动表面。图7显示了分别为实线和虚线的GSI = 50,mi = 10,D = 1.0和GSI = 10,mi = 10,D = 0.0的Hoek-Brown屈服面。从图7a中可以看出,虚线在sigma;3/sigma;ci的低水平时略低于实线。随着sigma;3/sigma;ci增大,两条线会聚,然后在图7b中显示的点A之后,虚线高于实线。图7显示这两个屈服面之间的差异并不明显。图7所示的点是从不同倾斜角和强度参数的数值下界解的塑性区得到的应力条件。在图7a中,可以看出,所有的十字符号都落在法向应力的较低水平,其中虚线在beta;= 45°的情况下低于实线。这意味着GSI = 10,mi = 10,D = 0.0的岩体在GSI = 50,mi = 10,D = 1.0(在图7a中用圆圈符号表示)的情况下产生较低的载荷。这已在图5中证明,其中GSI = 10,mi = 10,D = 0.0的稳定性数目大于GSI = 50,mi = 10,D = 1.0的稳定性数目
全文共12406字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[16361],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


