
英语原文共 14 页,剩余内容已隐藏,支付完成后下载完整资料
等距离约束度量学习的人重新识别技术
Jin Wang(a), Zheng Wang(b), Chao Liang(b), Changxin Gao(a), Nong Sang(a)
(a)华中科技大学自动化学院,武汉430074
(b)武汉大学计算机学院,武汉430074
文章信息
文章历史:
2016年7月1日收到
2017年8月3日修订
2017年9月7日接受
2017年9月9日在线提供
关键词:
人重新识别
度量学习
等距离嵌入
摘要
行人重新识别(re-id),目的是在不相重叠的相机网络中搜索一个特定的行人,近年来行人重识别受到广泛关注。这个任务非常具有挑战性,特别是当数据库中每个人只存在单个图像时。本文提出了一种基于学习马氏距离的算法来研究行人重识别技术。我们的方法有两个显著的特点:(1)为了获得训练数据的最佳可分离性,我们首先通过将类间距离强制为零来最大限度地减小内部类距离,(2)提高学习度的泛化能力,然后最大化不同类之间的最小边界。在简单的几何直观的启发下,一个规则的单纯性最大化了它的最小边长,提供了所有边长的总和,我们的方法,称为等距离约束的度量学习(EquiDML),应用最小二乘回归技术将同一个人的图像映射到一个规律的单形同一顶点,并将不同的人的图像映射到一个规律的单形不同顶点。因此,在已学指标下,相同类别的图像被折叠到单个点,而不同类别的图像被转换成等距。这个简单的想法被进一步表述为凸凹性问题,由投影梯度下降法解决,并被证明在行人重识别中非常有效。尽管它相当简单,但我们的方法在CUHK01、CUHK03、Market1501和DukeMTMC-reID数据集上的表现优于最先进的方法,并在广泛使用的VIPeR数据集上取得了非常有竞争力的表现。
1.介绍
行人重识别[1-3](re-id),目的是在一个不相重叠的摄像头网络中搜索一个特定的人。近年来,由于其在视频监视和公共安全方面的重要应用(例如,交叉相机跟踪[9]、法医搜索[10]和多摄像机行为分析[11]),该任务已经越来越受到计算机视觉行业[1,4 - 8]的注意。在行人重识别中,行人个体的外观是主要的利用信息,因为一般在典型的监控场景中,人脸、步态或指纹等更可靠的生物特征并不总是可用的[12]。然而,由于不同相机间视点的变化、个体身体部位的部分遮挡、光照条件的变化和背景杂波的变化的影响,个体的外观可能会有很大差异。尽管计算机视觉的研究人员做出了相当大的努力,但由于其在公共数据集上的技术水平有限[7,13-15],行人识别问题还远未得到解决。
一般来说,人的重新识别可以看作是视觉检索问题的一项特殊任务,例如:在给定一个探测出的行人图像的后,系统根据其与探测的相似性得分对数据库中的所有行人的图像进行排序,然后将最相似的图像返回给用户进行进一步验证。通常,它包含在行人重识别中的两个主要部分:描述行人图像的高质量特性描述,以及一个健壮的相似性或度量函数来进行行人匹配。
一个精准的行人重识别非常依赖于高质量的行人特征描述。一个好的行人特征描述应该区别于类别间的特征,同时对类别内变动具有鲁棒性。近年来,已有许多关于视觉特征提取和鲁棒性表征的研究成果,如SCNCD[16]、gBiCov[17]、mid-level filters [18]、LOMO[19]和GoG[20]等。然而,通常很难构造出一个描述符同时具有识别性和鲁棒性的交叉视图变化,这是通过对不同特征的综合评价来证明的[21]。
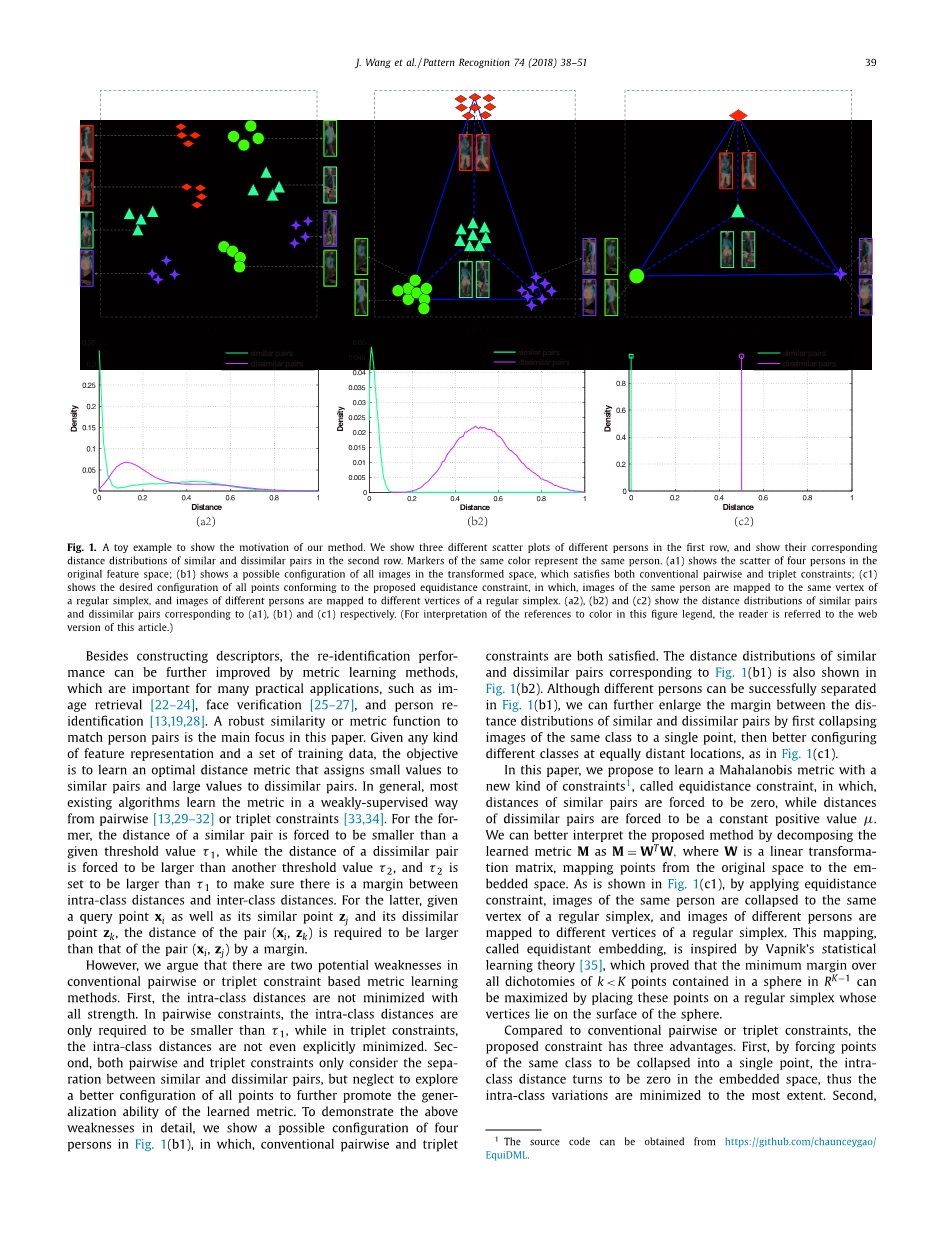
图1.用一个例子来说明这个方法的原理。我们展示了第一行中不同人的三个不同散点图,并在第二行中显示了相似和不相似对的相应距离分布。(a1)表示四个人在原始特征空间中的散布;(b1)显示了变换空间中所有图像的可能配置,它满足了传统的成对和三重约束;(c1)显示了符合所提出的等距离约束的所有点的所需配置,其中,同一人的图像是映射到常规单形的相同顶点,而不同人物的图像被映射到常规单形的不同顶点。(a2),(b2)和(c2)分别表示对应于(a1),(b1)和(c1)的相似对和不相似对的距离分布。(为了解释本图例中对颜色的引用,读者可参考本文的网页版。)
除了构造描述符之外,通过度量学习方法可以进一步提高重识别性能,这对于许多实际应用很重要,如图像检索[22-24],人脸识别[25-27]行人重识别[13,19,28]。本文主要关注一个强大的相似度或度量函数来匹配一对行人。给定任何类型的特征表示和一组训练数据,目标是学习一个最佳距离度量,将相似对和较大值分配给不同对。一般来说,大部分现有算法通过成对[13,29-32]或三重约束[33,34]的弱监督方式学习度量。对于前者,迫使相似对的距离小于给定阈值tau;1,而不相似对的距离被迫大于另一阈值tau;2,并且tau;2是设置为大于tau;1以确保类内距离和类间距离之间存在余量。对于后者,给定一个查询点xi及其相似点zj及其相异点zk,该对(xi,zk)的距离需要大于该对(xi,zj)的距离一个余量。
然而,我们认为传统的基于两两或三重约束的度量学习方法存在两个潜在的弱点。首先,所有的操作都不会使类内的距离最小化。在成对约束中,类内距离只需要小于tau;1,而在三重约束中,类内距离甚至没有明确地最小化。其次,成对和三重约束只考虑相似和不相似对之间的分离,而忽略了对所有点的更好配置以进一步提高学习度量的泛化能力。为了详细证明上述弱点,我们在图1(b1)中示出了四个人的可能配置,其中,传统的成对和三重约束都满足。图1(b2)也显示了与图1(b1)相对应的相似和不相似对的距离分布。虽然不同的人可以在图1(b1)中成功地分离出来,但是我们可以进一步放大相似和不相似对的距离分布之间的差距,通过将同一类别的第一幅图像折叠为单一点,然后更好地配置不同的类别如图1(c1)所示。
在本文中,我们提出用一种新的约束来学习马氏距离度量,称为等距离约束,其中,相似对的距离被迫为零,而不相似对的距离被强制为一个恒定的正值mu; 。通过将学习量度M分解为,我们可以更好地解释所提出的方法,其中W是线性变换矩阵,从原始空间到嵌入空间的映射点。如图1(c1)所示,通过应用等距约束,同一个人的图像被折叠到普通单形的同一顶点,不同人的图像被映射到普通单形的不同顶点。这种称为等距离嵌入的映射受到了Vapnik的统计学习理论的启发[35],该理论证明了中包含在一个球体中的k lt;K点的所有二分的最小边界可以通过将这些点放在一个常规单形的顶点位于球体的表面上。
与传统的成对或三重约束相比,本文所提出的约束具有三个优点。首先,通过强制同一类别的点被折叠为单个点,类内的距离在嵌入空间中变为零,因此类内变体在最大程度上被最小化。第二,通过将不同类的点嵌入到不同的顶点,可以保证不同类之间的最佳可分性。最后,正如Vapnik [35]所证明的那样,这个等距嵌入最大化了类之间的最小一个反对余量边界,这可以提高学习度量的泛化能力。
这项研究的主要贡献可以概括如下:
(1)提出了一种等距离约束的新度量学习方法。 通过将相似对映射到常规单形的同一顶点,并将不相似对映射到常规单形的不同顶点,可以提高训练数据的可分离性和学习度量的泛化能力。
(2)等距离约束由平方损失编码,并进一步表示为具有正半精确(PSD)约束的凸优化问题。我们证明了这个问题可以通过投影梯度下降法得到有效解决。
(3)对五个人重新识别基准进行了大量的实验,包括VIPeR,CUHK01,CUHK03,Market1501和DukeMTMC-reID,表明这种简单的方法胜过了其他最先进的方法。 此外,还提出了对所提出方法的全面分析。
本文的其余部分安排如下。第2节介绍相关工作。第3节详细解释了我们的方法。第4节对三个数据集上最先进的算法进行了广泛比较,本节还介绍了我们的方法分析。最后,我们在第5节总结本文。
2.相关工作
近年来,已经提出了许多度量学习方法来在不同的相机视图中匹配行人。根据不同的配置和优化标准,这些方法大致可以分为三组。以Keep It Simple and Sraightforward Metric Learning(KISSME)[27]和Cross-view Quadratic Discriminant Analysis(XQDA)[19]为代表的第一组,将度量学习问题制定为分别估计两个类别的两个高斯分布,并且通过考虑两个高斯分布的对数似然比检验,可以相应地获得简化且非常有效的解决方案。第二类包括局部Fisher判别分析(LFDA)[36],正则相关分析(RCCA)[37],边缘Fisher分析[38,39]和零空间[14],重点研究区分子空间,因为通过将学习的度量分解为,原始空间中的马氏距离可以被看作变换子空间中的欧几里德距离。这些方法通常具有封闭形式的解决方案,这在实际应用中非常有吸引力。第三组旨在从一组距离约束中学习PSD马氏距离度量[13,29-34]。一般来说,对这些方法的监督由(a)成对约束[13,29-32]给出,它强制正对之间的距离较小,负对之间的距离较大,或者(b)三重约束[33,34],通过限制负对之间的距离大于相同探针图像的正对之间的距离。
在成对约束方法中,成对约束分量分析(PCCA)[31],Logistic判别度量学习(LDML)[29]和有效PSD约束非对称度量学习(MLAPG)[13]是三种代表性方法。 PCCA[31]算法采用广义逻辑函数作为损失函数,并从高维输入空间中的稀疏成对相似/不相似约束中学习投影矩阵。LDML[29]算法应用Logistic判别函数来模拟样本是否属于同一类别的概率。MLAPG[13]算法明确地模拟了PSD约束,并引入了非对称样本加权策略来解决样本不平衡问题。由于负对在很大程度上多于正对,因此在基于成对约束的方法中存在严重的样本不平衡问题。 PCCA算法随机放弃一些负对来平衡训练样本,这可能不是最佳解决方案,因为判别信息没有被充分利用。建议在MLAPG中引入不对称权重的策略[13],并且在个人重新识别任务中被验证为非常有效。大边缘最近邻(LMNN)[33]度量学习方法是使用三重约束的代表性方法。它试图通过拉动位于k个最近邻居内的正样本,同时向远处大量推送负样本来学习马氏距离度量。
考虑到每个单独约束中涉及的图像数量,所提出的等距离约束也可以被看作是一种特殊的成对约束。所提出的EquiDML方法与上述方法之间的主要区别在于每个约束的内容。我们的方法迫使类内距离为零,类间距离为常数正值,旨在获得训练数据的最佳可分性,同时通过最大化不同类之间的一对多关系,最大化提高学习度量的泛化能力。与上述方法不同,我们只是使用平方损失函数来编码每个单独的约束。 也采用与MLAPG [13]相同的不对称加权策略来解决数据不平衡问题。
我们的方法也可以用数据嵌入的方式来解释,其中来自同一类的样本被折叠成规则单形的单个顶点,而来自不同类的样本被映射到常规单形的不同顶点。这种嵌入被称为等距离嵌入,以前在线性回归分析(LAR)[40]中采用这种嵌入来解决每个主题的单个图库样本的人脸识别问题。 但是,我们的方法与LRA完全不同。 LAR方法旨在学习映射矩阵以将画廊样本嵌入到等距离的位置,其制定方式与指标矩阵的线性回归相同。更重要的是,LRA方法是专门设计来解决单样本人脸识别问题的,不能直接应用于行人重识别,这是一种行人验证工作。
3.我们的方法
3.1等距离约束的度量学习
为了便于表达,我们在[13]此使用符号来描述我们的方法。 假设我们有一个交叉视图训练集,其中在一个d维空间中包含n个样本,其中在同一个d维空间中包含m个样本,但是从另一个视角来看,是和之间的匹配标签,其中表示和来自同一类,否则。我们定义相似集合和不相似集合和。如果图像对的匹配标签,则称该图像对为相似对,否则称为不相似对。
基于训练集,我们旨在学习马氏距离函数[41]来测量两幅图像之间的距离:
其中是度量有效性的正半确定(PSD)矩阵。 通常,度量学习的监督由成对约束[13,31]或三重约束[3,33]给出。
成对约束通常被定义为:
和是两个预先设定的阀值,且。
对于三重约束,我们给出了一组三元组,其中且,并且度量通过以下约束学习:
这意味着负对之间的距离应该大于正对之间的距离至少为。成对约束和三重约束考虑了正对和负对之间的可分性。
我们提出通过将类间距离固定为常数值并将类内距离最小化为零来学习度量:
其中是一个恒定的正值。直观地说,等距约束说明了三件事情。首先,正对被折叠成一个点。其次,类间距离应该大于类内距离,这确保了正对和负对之间的可分性。第三,由于任何不同对的距离必须是相同的恒定值,所以不同的人应该在变换后的空间中等距离的地方分布。
为了学习这样的度量,我们采用平方损失函数对两个约束进行编码。相应地,整体损失函数是:
其中和分别是和中元素的总数,是在范围内的超参数,控制两个力的平衡:一个将类内距离最小化为零,另一个迫使类间距离是一个常数值。
然而,我们观察发现,上述损失函数不利于直接优化行人重识别的性能。问题来自正对的损失函数。在图2中,我们绘制了正对的三种不同损失函数。它们分别是平方损耗,线性损耗d和移动平方损耗。如图2所示,损耗的平方在0附近减慢得太慢,甚至比线性损耗还要慢,这将延长收敛时间。因此,我们简单地采用移位平方损失作为正对损失函数。通过去除损失函数中的常数值,总损失被表达为:
是防
全文共28825字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[16333],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


