
英语原文共 12 页,剩余内容已隐藏,支付完成后下载完整资料
众包系统中的在线成本敏感型决策方法
Jinyang Gaodagger;, Xuan Liudagger;, Beng Chin Ooidagger;, Haixun Wangsect;, Gang ChenDagger;
dagger;School of Computing, National University of Singapore, Singapore sect;Microsoft Research Asia, Beijing, P.R. China Dagger;College of Computer Science, Zhejiang University, Hangzhou, P.R. China
dagger;{jinyang.gao, liuxuan, ooibc}@comp.nus.edu.sg, sect;haixunw@microsoft.com, Dagger;cg@zju.edu.cn
摘要
众包通过利用人类智能为许多挑战性问题创造了各种机会。例如,图像标记、自然语言处理和基于语义的信息检索等应用可以利用基于人群的人类计算来补充现有的计算算法。很自然地,众包中的人力工作者根据他们的知识、经验和看法来解决问题。因此,不清楚哪些问题可以通过众包更好地解决,而不是单纯使用传统的基于机器的方法来解决。因此,需要一种成本敏感的定量分析方法。
在本文中,我们设计和实施了众包的成本敏感方法。我们在线估算人群采购工作的利润,从而终止那些没有未来利润的问题。提出了两种模型来估计众包工作的利润,即线性模型和广义非线性模型。使用这些模型,根据已收到的答案计算为特定查询获得新答案的预期收益。如果获得更多答案的边际预期利润不是正值,则问题会实时终止。我们扩展了在HIT中发布一批问题的方法。我们使用AMT上的两个现实世界作业来评估我们提出的方法的有效性。实验结果表明,我们提出的方法胜过所有最先进的方法。
类别和主题描述
H.3.m [信息存储和检索]:杂项
关键词
众包,决策
1.引言
作为利用基于人群的人类计算和智能的平台,众包引起了极大的兴趣。 它在某种程度上受到Web 2.0社区大量合作的启发,用户不仅分享信息,还分享他们的知识和智慧。 诸如亚马逊Mechanical Turk(AMT)[1]这样的平台通过将兼容工作交给工作人员来促进数据的完善和噪音的减少。 这些复杂的工作包括图像标记,基于语义的信息检索和自然语言处理,这些对于计算机来说很难,但对于人类工作者相对容易。 与其设计复杂的算法或花费大量资金来咨询专家,许多这些工作可以通过众包平台上的人工以更低的成本解决。 最近出现的一些成功的众包应用包括CrowdDB [4],CrowdSearch [19]和HumanGS [14]。
尽管众包系统取得成功,但由于三个原因,采用群众采购仍然非常具有挑战性。首先,对于大多数众包工作,我们需要获得多个答案以保证其质量。因此,我们必须决定何时停止获得由人类工作者提供的新结果。大多数现有工作使用精度或成本作为优化目标。这些在实践中变得过于僵硬。然而,权衡并非微不足道。典型地,众包工作可能具有不同的难度(例如,孩子的家庭作业与研究问题),风险(例如Flickr图像标签与癌症诊断)和利润(例如针对个人兴趣的调查与投资模型的设计)。因此,建立一个考虑众包工作的所有这些因素的在线经济模型是很重要的。
其次,目前的研究都没有关注问题是否适合众包。直观地说,基于众包的技术更适合需要进行海量处理的问题。例如,情感分析,图像标记和信息检索对于众包而言是很好的问题,而大型数值分析则可以更好地处理机器。
最后,众包质量的评估仍然是最重要的。低质量的答案可能会大大降低众包的质量,并引入噪声。为了解决质量问题,已经提出了几种方法,如Crowdscreen [12]和CDAS [9]。这两项建议都只考虑了工人提供的反馈的准确性,而没有考虑到任务的难度。然而,要预测任务的难度是非常具有挑战性的,并且需要一个能够处理各种难度等级的问题的稳健算法,以及各种质量等级的答案。
在本文中,我们提出了一种新的在线成本敏感型决策模型来解决上述三个挑战。我们的贡献包括:
bull;我们提出了一个在线,成本敏感的决策模型来分析和决定是否停止问题的现状,考虑到问题的价值,获得不正确答案的风险以及众包系统。据我们所知,我们的模型是第一个提供在线量化利润分析的众包工作。我们进一步扩展我们的算法,以支持约束条件下的在线成本敏感型决策,如有限预算等。
bull;应用程序或任务可能包含各种难度级别的问题。我们提出了一个测量问题难度的模型,我们设计和实现了一个处理这些问题的稳健算法。
bull;我们提出了一种称为精度 - 成本的新算法,用于形成众包中准确性和成本的边际分析。该算法计算工人数量增加时的增量亲合度。
bull;我们对从AMT工作人员的答案中获得的两个实际数据集进行了广泛的实验研究,以评估我们提出的方法的有效性。结果表明,我们的方法在保持低成本的同时获得了精确的结果。我们还开发了一种自动问题分发方法,可以在HIT中分配多个问题,同时可以随时终止每个问题。
本文的其余部分安排如下:第2节概述了我们的方法, 第3节解释了必要的准备, 第4部分介绍我们提出的线性模型,以获得实时决策并分析利润。 第五部分将我们的线性模型扩展到非线性模型,它证明了成本和准确性之间的关系,并为我们的模型提供了广泛的适用性,第6节讨论了实验研究,第7部分回顾了相关的工作。 最后,我们在第8节中总结。
2.概述
在本节中,我们将概述我们成本敏感的众包决策方法。
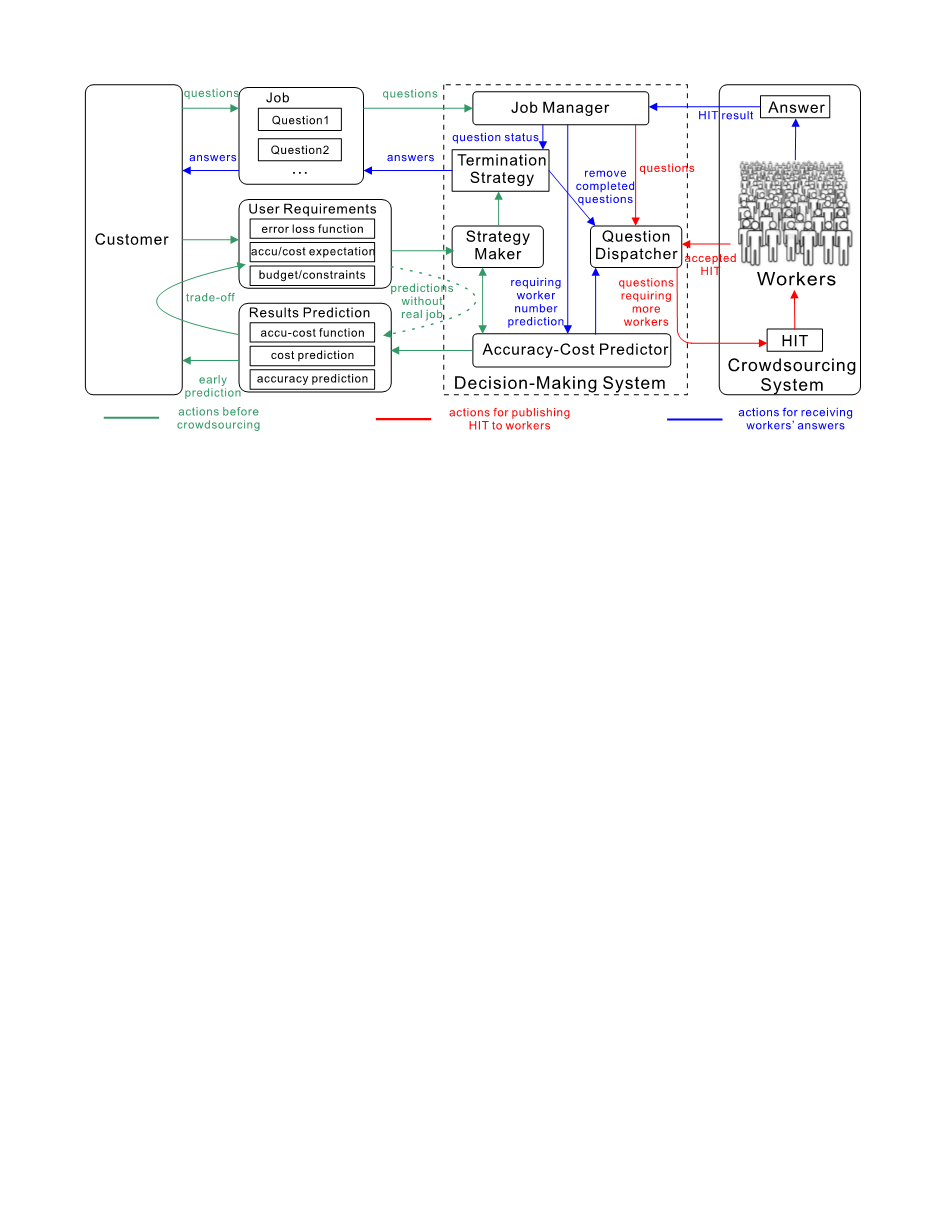
图1显示了我们提出的方法的体系结构。核心部分是决策系统(虚线框),由五部分组成,即工作管理者、问题调度员、准确度成本预测器、策略制定者和终止策略管理者。工作经理将众包客户的问题传递给问题调度员。它不断收集工作人员的答案,并将更新的问题状态报告给终止策略经理。在收到问题后,问题调度员使用问题调度算法将这些问题分配给几个工作人员(将在5.2节讨论)。终止策略经理确定我们是否应该停止针对某个问题获取更多答案,并根据问题的状态将结果返回给客户。这些终止策略由策略制定者根据用户的要求产生,即错误损失函数,准确性/成本期望,预算或其他约束条件。战略制定者采用我们在第4节中提出的线性模型。注意,生成的策略存储在终止策略管理器中,这样我们的决策系统就能够决定是否应该实时终止问题。精度 - 成本预测器提供了两个主要功能。首先,它预测结果以及准确性/成本比。其次,它与战略制定者一起使用广义非线性模型生成终止策略。第5节讨论了非线性模型的细节。
总之,我们提出的决策系统会自动向工作人员发送问题。它终止问题并根据生成的终止策略实时返回答案。这个决策系统还可以在运行真正的众包工作之前对结果进行早期预测,以帮助客户设置正确的用户需求。在接下来的部分中,我们将介绍实施这个决策制定系统的想法和方法。
3.预备
在第4节和第5节描述我们的方法之前,我们讨论需要的先验知识来理解问题。
为了简洁起见,在我们的模型中,我们假设问题是双选问题。我们可以将这两种选择看作二元值0和1.但是,我们可以很容易地将我们的方法扩展到有两种以上选择的问题。
问题状态:我们通过一对 (m, l) 对问题的状态进行建模,该对表示从工人接收到的两个不同答案的数量。由于值0和1只是代表两种选择的两个符号,因此可以交换答案中的0和1。结果,以下两种情况:(1) m 0s 和 l 1s; (2)m 1s和 l 0s可以看作是相同的,表示工人对这两种选择的一致意见。在不失一般性的情况下,在本文的其余部分,我们用(m,l)(mgt; 1)来表示上述两种情况。
直观上,问题状态表明问题的难度。当m远大于l时,大多数工作人员就一个选择达成一致。这可能是这个问题很容易。另一方面,当m接近1时,这个问题可能太难以让工作人员猜测了。
问题解答:问题解答是一系列问题的核心,因为我们从这个问题的工人那里得到答案,
r = {(m0, l0), (m1, l1), · · · , (mN, lN)}
其中(m0,l0)=(0,0)是初始状态。每一个非初始状态(mi,li)的回答都比之前的状态多一个
(mi-1,li-1),即(mi,li)=(mi-1,li-1 1)或(mi-1 1,li-1)。在上面的问题运行r中,问题在问题状态(mN,lN)处终止,之后它不会接受更多答案。例如,{(0, 0), (1, 0), (2, 0), (2, 1)}是一个有效的问题运行,它在得到三个答案后停止,但 {(0, 0), (1, 0), (2, 1), (2, 0)}不是有效的问题运行。
问题答案的准确性:我们使用AQ来表示Q问题答案的准确性,即工作人员提供正确答案的可能性。考虑到答案的准确性的大多数现有作品假设准确度是可以从采样答案中计算的固定值,例如, [9] [12]。这些模型的主要缺点是他们不考虑问题的难度。使用这些模型,对于单个员工,他对不同问题的回答将具有相同的质量。然而,这一观察结果与直觉相矛盾,即一个难题的答案可能很差。
在我们的论文中,我们不是将精度建模为单个修正值,而是采用基于抽样的方法来估计这个值,我们将精度表示为概率分布。概率分布提供了基于观察到的问题状态建模答案质量的能力。我们将精度AQ建模为随机变量,我们通过观察问题状态(m,l)来估计AQ的值。具体来说,我们假设AQ服从Beta分布:
假设问题1.给定问题Q,AQ的概率密度函数为:
f (AQ = micro;) = micro;Aminus;1(1 minus; micro;)Bminus;1/Beta(a, b)
因此我们有E [AQ] = a /(a b)。 a和b是Beta分布的参数,代表了随机变量的先前预测。 Beta分布实际上是一个二维Dirichlet分布1。我们可以用更一般的Dirichlet分布代替Beta分布来解决多项选择问题。
如果先验分布是B(mu;| 1,1),即均匀分布,那么AQ的估计只能通过观察问题状态来确定。换句话说,我们的方法是传统的固定准确度模型和单形分布的一种广义形式。考虑到事先知识和问题状态观察,以适应估计的问题分布。理想情况下,当估计分布与问题难度的经验分布相同时,估计分布表现最好。然而,实证分配总是难以获得。而且,基于经验分布来计算贝叶斯推断是不可行的。 Beta分布用于简化计算,因为它是二项分布和伯努利分布的共轭先验分布。另一方面,具有适当参数的Beta分布恰好符合精度分布。
我们观察到,由于使用不同的先前预测参数a,b几乎不会改变结果,所以我们的模型是鲁棒的。这是因为我们的模型是基于概率分布的,并且可以适应性调整以适用于具有多种困难的问题。此外,我们观察到AQ在几个实际问题集中的经验分布,包括推特分析问题和我们实验中使用的常识问题,与B(mu;| 6,2)分布类似。另一方面,我们的实验也表明,当分布发生变化时,这一估计仍然有效。在第4节中,我们解释了基于概率分布的精度模型优于基于固定值的精度模型的原因。在实验部分,我们使用经验数据来支持上述两个观察。
问题结果的准确性:我们使用AR来表示基于当前问题状态(m,l)的多数表决结果的准确性。我们总是选择由多数m代表的答案。因此,AR是主要人选择正确答案的概率。我们将(x,y)定义为具有x个正确答案和y个不正确答案的状态。由于状态(m,l)表示m个正确答案或m个不正确答案,。通过贝叶斯分析,条件概率AR给定AQ和观测值(m,l)为:
注意AR也是一个随机变量,因为AQ是一个随机变量。
表1列出了本文后面几节中使用的简谱。
4.线性决策
在本节中,我们介绍一个用于在线决策的线性模型。 我们首先根据问题状态和事先分配估计答案的准确性。 根据对答案准确性的估计,我们获得每个状态的边际收入和利润。 这使我们能够根据经济利润在每种状态下做出决定。 在本文中,我们采用动态规划算法来计算利润,并为每个问题状态制定策略。 我们证明了我们的策略生成算法的时间复杂度为O(n2)(n是单个问题的最大可能答案数量,即搜索空间),与现有方法如CrowdScreen的O(n4)线性编程。 在本节中,我们还讨论了扩展我们的方法以解决更复杂的问题的技术,即具有准确性和成本约束的线性模型。
4.1线性模型
对于问题Q,线性模型有三个变量:问题值VQ,误差损失LQ和每个工人的问题成本CQ。
如第2节所述,这些值由众包客户预设。 VQ是给出答案的这个问题的价值(不一定是正确的)。误差损失LQ是
全文共18616字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[16098],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


