90°旋转二维条带装箱问题的启发式算法外文翻译资料

 2022-03-18 22:33:19

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

90°旋转二维条带装箱问题的启发式算法

何琨，金燕，黄文奇 计算机科学与技术学院 华中科技大学 武汉 430074

摘要

针对二维条带装箱问题，本文提出了一种确定性启发式算法（DHA），该算法允许块90°旋转，且不存在切割约束。目标是将所有不重叠的块都放置在一个给定宽度的条带中，这样可以将工件的总高度最小化。基于动作空间的定义，提出了一种新的候选位置的排序规则，使得当前块的位置尽可能地低，和其他内部块尽可能地靠近，并且对进一步放置的不利影响越小越好。四组基准实验表明，与文献中最先进的算法相比，提出的DHA取得了更有竞争力的结果。此外，作为一种确定性算法，DHA可以在小规模和大规模问题实例上只通过一次独立运行就可以获得高质量的解决方案，并且结果是可重复的。

关键字：组合优化；条带装箱；启发式算法；确定性算法

  1. 绪论

二维条带装箱问题（2D-SPP）是一个开放维度问题，一组矩形件必须垂直放进一个固定的宽度和无限的高度的矩形条带里，并尽量使工件总高度最小。这个问题是一个重要的NP难问题，在许多行业，包括木材、玻璃、金属工业中有许多实际应用，其目的是在合理的时间内找到很好的解决方案。为了满足不同行业的制造需求，可以考虑方向约束和切割约束。方向约束包括两个情况：所有块的方向是固定的或者当它们被放进条带中时工件块可以旋转90°。关于切割问题，有两种描述，即有切割的包装和无切割的包装，详细信息可以参考Christofides和Whitlock（1977）。在本文中，我们假设工件可以90°旋转，并考虑无切割包装。

2D-SPP是一个具有挑战性的问题，近几十年来一直被研究人员广泛研究。文献中提出的算法可以分为精确算法和启发式算法两大类。

研究人员提出了一些启发式算法来求解2D-SPP，包括由Baker, Coffman和Rivest (1980)提出的左下角的算法，由Chazelle (1983)提出的左下角填充算法，由Burke, Kendall和Whitwell (2004)提出的最佳适应算法以及由Wu, Huang, Lau, Wong和Young (2002)提出的灵活性第一算法。然后Burke, Kendall和Whitwell (2006)将最佳适应启发式算法（BF）与禁忌搜索（TS）、模拟退火（SA）和遗传算法（GA）结合起来分别提出了三种新算法：BF TS， BF SA 和BF GA。Zhang, Kang和Deng (2006)提出了一种启发式递归算法(HR)。 Huang和Chen (2007)提出了一种基于崩落度的启发式算法(HA)。Alvarez-Valdes, Parrentilde;o和Tamarit (2008)提出了一种随机自适应搜索贪婪算法(GRASP)。Belov, Scheithauer和Mukhacheva (2008)提出了SubKP和BLR算法，以及Burke, Hyde和Kendall (2011) 提出了车轮优化算法（Squeaky wheel）。Leung和Zhang (2011) 提出了一种基于层的快速启发式算法（FH）。

据我们所知，GRASP, SVC, BF TS, BF SA, BF GA 和FH是文献中最先进的启发式算法。GRASP算法将构造阶段和改进阶段相结合，构造阶段选取了一个有用的工件块来放置，改进阶段纠正了一些错误的决定以改进解决方案。SVC算法通过求解一维背包问题来填充空空间，并在块的宽度上分配适当的伪利润。BF TS, BF SA和BF GA基于该最佳拟合启发算法分别应用了禁忌搜索、模拟退火算法和遗传搜索。FH算法主要是基于来自瓦工砌墙规则灵感的启发式策略。

与启发式方法的结果比较，精确算法有有限个结果，这些精确算法包括Christofides和Hadjiconstantinou1995年提出的算法，崔、杨、程和宋2008年提出的算法，Kenmochi, Imamichi, Nonobe, Yagiura和Nagamochi2009年提出的算法，Lesh, Marks, McMahon和Mitzenmacher2004年提出的算法，Martello, Monaci和Vigo2003年提出的算法。然而，由于运行时间和计算机内存的限制，这些精确算法仍然不能有效地处理大规模数据集的问题。

据我们所知，最有效的精确算法是由Kenmochi等人2009年提出的阶梯和G-阶梯算法。他们把阶梯位置作为分支操作，把动态规划作为边界操作，这样他们就可以处理大多数数据集，包括49个矩形块和多达500个块的数据集。与其它精确算法相比，求解实例的规模要大得多。

根据结果是否可重复，可以将启发式算法分为两类，即随机算法和确定性算法。BF TS, BF SA, BF GA, HR, GRASP, SVC和BLR属于前者，而HA, FH 和Squeaky wheel属于后者。

在本文中，基于条带装箱问题的特点提出了一种新的确定性启发式算法（DHA）解决2D-SPP问题。DHA集成了一个快速构建阶段和局部树搜索阶段，这两个关键要素一起来确保高效率的性能。首先，我们为所有候选位置定义了一个新的排序规则，使得当前工件块的位置尽可能地低，当前块与已放置的其他工件块之间的距离尽可能地接近，并且对进一步放置的不利影响尽可能小。此外，我们还应用了局部树搜索法来改进解。在每一次迭代步骤中，我们选择顶部N个有希望的位置分别伪执行它们，继续伪放置其他块，直到所有的块都被放置到条带中以获得一个临时的高度。然后，我们在N个位置中选择一个最小临时高度的位置来执行。

我们在文献中对四组实例进行了DHA性能评价，包括小数据集和大数据集。计算结果表明，DHA可以在合理时间内获得高质量的解决方案。与其他国家的最先进的算法的比较也表明，DHA是具有高度竞争力的。

论文的剩余部分组织如下：第2节给出了二维条带装箱问题的具体描述；在第3节中，定义了一些重要的概念，然后描述了我们的算法的组成部分，包括构造阶段和搜索阶段；第4节专门讨论计算结果，并在第5节给出结束语。

  1. 问题详述

设一个具有固定宽度W和无限高度的矩形条S，考虑将S嵌入到二维笛卡尔坐标系中，使得左下角与原点重合。假设有n个矩形块将被放置在条带中，每一个矩形块都i有宽度wi和高度hi，目的是把所有n个矩形块没有重叠的放到条带中，使矩形块的总高度最小。

为了将每个矩形块i放入条带中，设(xi1,yi1) 和 (xi2,yi2) 分别表示左下和右上顶点的坐标。然后，问题可以表述如下：

在约束1到3中，i, j适用于1,2,hellip;,n和ine;j。约束1意味着每一个矩形块都应该垂直放置在条带中，约束2防止任何两矩形块重叠，约束3要求所有块都完全放进条带中。放置应满足这三个约束条件，其目标是将所有的n个矩形块放置在条带中，使矩形块的总高度最小化。

  1. 确定性启发式算法

确定性启发式算法（DHA）包含两个阶段：快速构建阶段和局部树搜索阶段。在构建阶段，DHA用贪婪算法放置矩形块，其总体目标是使所有放置件的高度尽可能低。此外，DHA总是使放置件尽可能靠近其他放置的矩形块，并尽量减小对接下来放置的不利影响。在局部树搜索阶段，DHA应用深度优先搜索来寻找最有前景的布局。通过伪执行和构建阶段，分别比较不同放置的最终总高度，DHA根据评价标准选择最好的放置并回溯到执行的当前位置。

我们首先定义了DHA所使用的几个重要概念，并描述了DHA的一般框架。然后详细介绍了构建阶段，并简要介绍了局部树搜索阶段。

3.1定义

定义1（配置）：假设在当前时刻，已经有一些矩形块被放进了条带中，而其他的等待被放置，这称为配置。我们通过矩形块和条带空隙的排列列表提出一次配置。如果条带中没有矩形块，我们称之为初始配置。如果所有的矩形块都被放置在条带中，我们称之为最终配置。

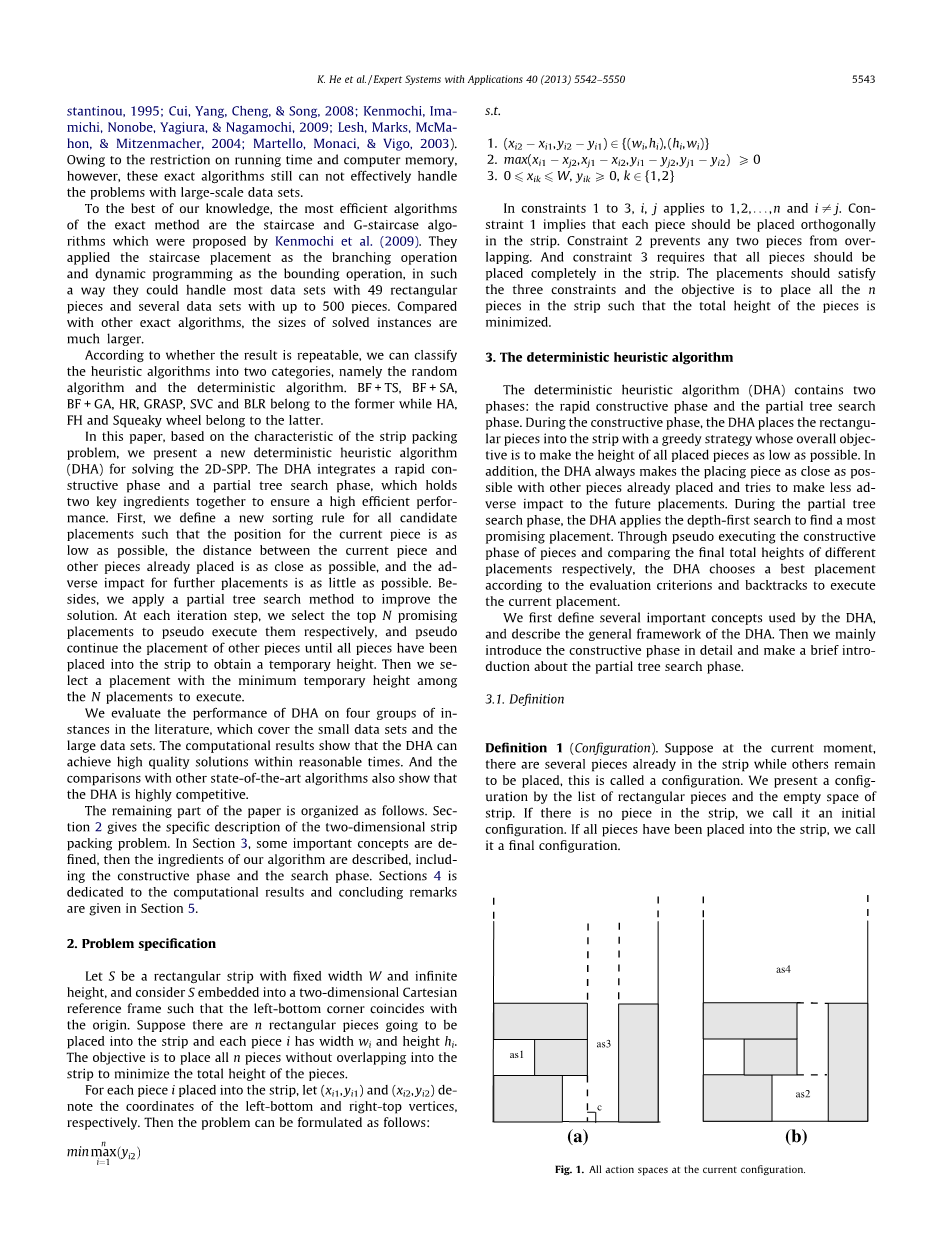
定义2（动作空间）：在当前配置中，我们可以将条带中的空隙看作许多小矩形条带。这些小条带大小足够使左、右和下边缘分别贴近一个矩形块或外部大条带的一边，顶部是打开的或者被一个矩形块的底边封闭。这些小条带称为动作空间。

图1 当前配置中的所有动作空间

图1给出了当前配置中所有动作空间的示例。有四个动作的空间：1，AS3图1（a）中的as1、as3和图1（b）中的as2、as4。动作空间的定义由何、黄和靳 (2012)提出的BFA算法以及何、黄(2011)提出的FDA算法中的动作空间改编和延伸而来。然后基于以下两个思想对构造算法进行了改进。其中一个优点是没无需将矩形块从条带底部空隙到顶部空隙放置。我们通常会搜索所有动作空间来寻找执行的最佳位置，这样当某些外部矩形块最适合的时候，底部的空闲空间就可以适时被占用。另一个优点是我们在使用动作空间时会考虑更多的角（包括虚拟角），如图1（a）所示的C角，因此它扩大了搜索空间，从而提高了解的质量。

定义3（角动作）：在当前配置，一个动作空间只有两个角，角的方向是“”和“”。角动作是一个动作，把一个矩形块放在动作空间的一个角上，这样一个顶点与一个角正好重合。

然后，我们定义了一个新的标准来评估不同的角动作。

定义4（紧凑度）：紧凑度涉及四个指标，如公式（1）所示。

（1）

  1. 贴数pi表示有多少边贴紧动作空间的边（2le;pile;4），e -pi是pi的标准化。pi的值越大e -pi的值越小，即将放置的矩形块与已经放进条带的矩形块越近。
  2. 符号hi表示动作空间自条带底部的高度，hi越小，矩形块放置的高度越低。
  3. 符号ni表示矩形块放进条带后的动作空间数量，ni越小条带空闲空间就越光滑，下一个矩形块就越容易放置。
  4. 符号fi表示当前放置对未来放置的影响，fi与一个阈值vi有关。首先，根据以非升序排序的各矩形块的边长设置vi值，并在排序队列中选择30%点的长度作为vi值。然后，在一个角上放置一个矩形块后，我们选择一个新的动作空间，它的底部边与工件的边相等，然后研究新动作空间的宽度与这个阈值之间的绝对差值。我们认为较小的优先，因为它仍然是可能填补这个动作空间的块，这样的空间可能就不会被浪费或一个非常小的空间将被浪费。因此，fi越小，当前放置对未来放置的影响越小。

两个紧凑度可以在字典序中比较。紧凑度越小，放置越好。

3.2算法描述

在这部分中，我们详细介绍了DHA来解决条带装箱的问题。DHA应用快速构建阶段和局部树搜索阶段以确保高性能。构建阶段在DHA中起重要作用，影响DHA解的质量和计算时间。详细的构造阶段如算法1所示：

算法1：伪代码构造阶段

1：Input：矩形条带的宽度W，n个矩形块和条带的最佳已知高度hbk

2：Output：所实现的带的最小高度h及其相应解

3：0→h

4：初始化动作空间列表，其中一个动作空间与条带一致。

5：矩形块长边的总长度→H

6：所有边按非升序排列，计算阈值vi

7：while有矩形块在条带外do

8：将动作空间按其左下角顶点坐标y非降序排列。

9：将剩余块通过不同的方向找到所有的角动作将其伪放置在顶部的k个动作空间中

10：计算每个角动作的紧凑度

11：在字典序中选择一个角动作：lt;紧凑度 ，块区域 ，块高度 ，左下角顶点坐标x ，水平放置优先性gt;

12：repeat

13：更新动作空间

14：if动作空间被放置的块占用then

15：执行动作空间的替换

16：end if

17：if一个动作空间被其他更大的动作空间包括then

18：删除这个动作

全文共8302字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[16033]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章