
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
INTL JOURNAL OF ELECTRONICS AND TELECOMMUNICATIONS, 2016, VOL. 62, NO. 1, PP. 43–48
Manuscript received November 15, 2015; revised March, 2016. DOI: 10.1515/eletel-2016-0005
采样速率对PID控制器参数整定的影响Michal Laskawski, Miroslaw Wcislik
摘要 - 本文讨论了连续和离散PID控制器的自动控制系统分析。提出了一种调整连续控制器参数的方法,该方法根据ITAE标准是最优的。本文使用了上述方法调整参数的离散控制器的控制系统。显示了受控信号采样周期变化对控制质量的影响。表现出了控制信号采样率变化时离散PID控制器最优参数值的变化。
关键词-PID控制器,调节,最优控制,采样率。
1. 绪论
控制系统中采样周期选择的一般规则是使用已识别的控制系统模型的参数。参数通常是:Tmax - 主导时间常数,L - 传输延迟时间常数,T - 惯性时间常数[1],[2]。 还有根据一些已知的规则确定的采样周期与控制质量指标的关系,例如:ts-建立时间和tr-rise时间,[2],[3]。这些规则允许我们根据已识别的控制器参数(Ti-积分时间,Td-微分时间常数)来估计信号采样周期,并在以下文献中给出:[2],[4]。 所有这些规则都没有明确规定采样周期Delta;t应该使用什么值。 它们只能粗略估计间隔Delta;t的一个大致可接受值。对于离散控制系统的建模和分析,假定连续控制系统是参考系统。 它使分析控制信号采样周期对离散系统控制质量的影响和离散控制器最优设置的选择变得更加容易。 在连续系统中,控制器不断监控受控信号(过程值)和参考信号(设定值)。 根据这些信号它会产生一个控制信号。通常使用为连续控制器设计的方法来选择PI和PID控制器的设置[5],[6],[7]。 错误的选择连续的控制器参数会导致控制质量不佳。 如果选择的设置与定期响应输入信号的控制器一起使用,则控制质量会更差,就像离散控制器一样。 为了避免这种情况,使用考虑到的优化方法来选择控制器参数采样周期。 这种方法在文献[8]中提出,下一节将简要介绍。
II. OPTIMAL SETTINGS OF CONTINUOUS PI AND PID CONTROLERS
文献[8]中展示了一个带有连续PID控制器的闭环控制系统,分析结果如图1所示
图1.具有连续PID控制器的基本控制系统图。
该PID控制器具有以下公式: (1)
其中:Kc比例增益,Ti - 积分时间,Td - 微分时间,N - 无量纲系数。无量纲系数N的值由参考书目分析确定。 通常系数的值在2到30之间[9]。 假定N = 20 [8]。受控系统与具有传输延迟的一阶惯性模型具有动力学的相似。 (2) (2)
其中:K - 静态增益,T - 惯性时间常数,L - 传输延迟时间常数。
模型描述可以以令人满意的精度映射各种工业过程的动态。 它也可以模拟稳定状态。 传输延迟的存在允许近似可能不稳定的过程。ITAE(时间加权绝对误差的积分)被选为最优性标准[10]:
(3)
A.调整程序
设置PI和PID控制器的最佳参数的过程由以下步骤组成。
bull;首先,PID控制器的比例和微分部分断开。对于PI控制器,只有比例部分断开。
在该程序的这个阶段留下控制器的组成部分是该方法的一个独特功能。
它利用PI或PID控制器近似于目标系统特性的目标系统特性,并有助于选择最优控制器参数。
根据控制系统可以用模型(2)近似的假设,由串联积分控制器和模型(2)组成的开环控制系统的传递函数由下式描述:
(4)
其中:
光谱传递函数的模块如下:
(5)
其中:
bull;在程序的下一个阶段,增加控制器积分部分的增益,使闭环系统达到边界稳定。
在这个阶段,评估控制器最终增益Ki和控制变量y的持续振荡角频率omega;osc。根据这些参数并考虑到|GOomega;osc| = 1并确定近似模型的时间常数T. (6)
bull;系数theta;根据稳定边界上公式(5)的自变量的等式计算得出:
(7)
考虑到omega;oosc =omega;oscT,theta;系数由下式描述: (8)
bull;通过方程组(9)得到PI控制器的最优设置。 (9)
PID控制器的最佳设置由方程组10得出。 (10)
方程(9)和(10)是使用PI和PID最优设置的近似值获得的。 最小二乘法提高了最终结果的有效性。 由公式计算得theta;= [0.2,2]
B.推荐参数的设置对控制质量的影响
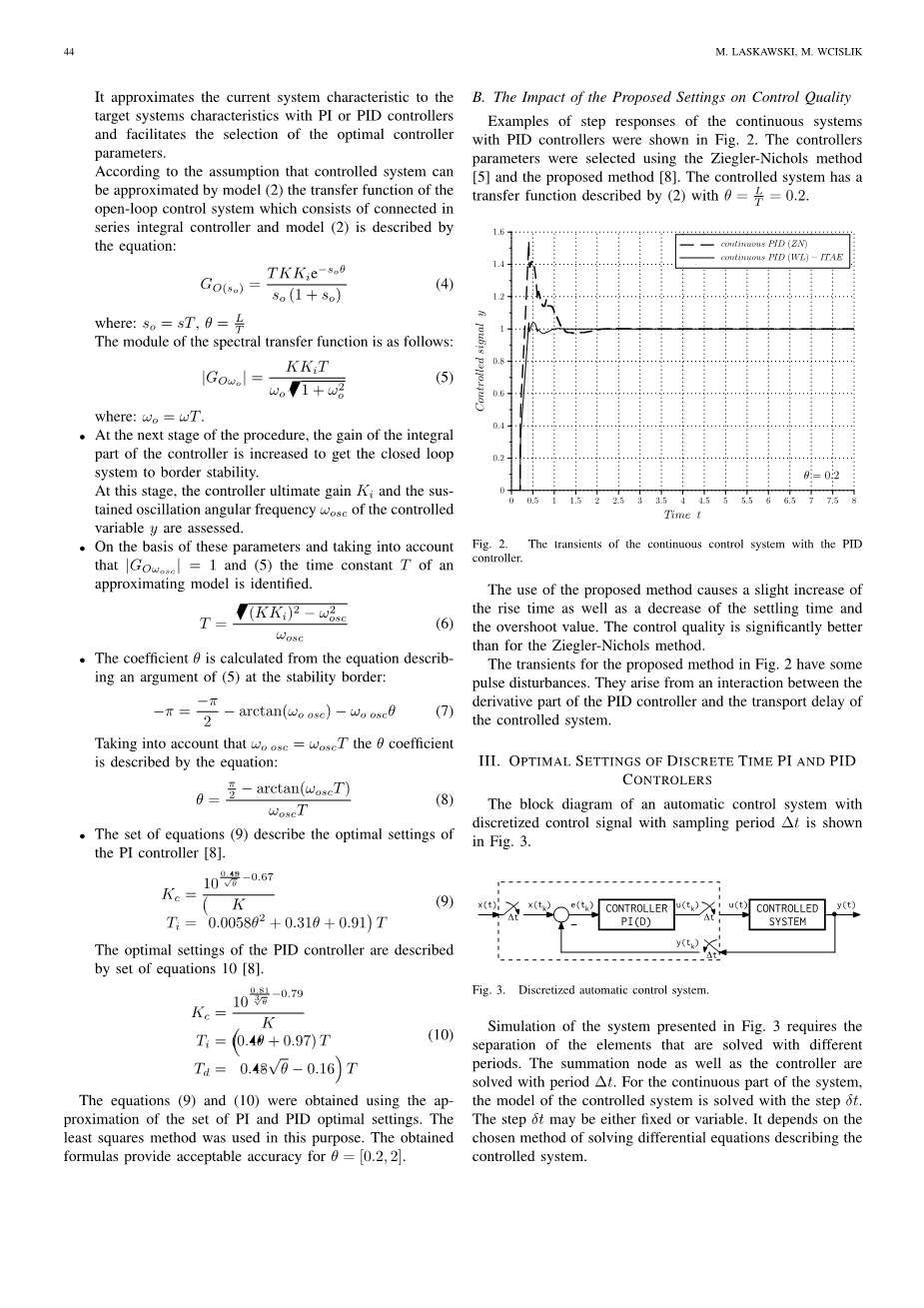
具有PID控制器的连续系统的阶跃响应实例如图2所示。控制器参数使用Ziegler-Nichols方法[5]和所提出的方法[8]进行选择。 受控系统具有(2)所述的传递函数。
Fig. 2. The transients of the continuous control system with the PID controller.
此方法实际使用上能够上升时间的轻微增加以及建立时间和过冲值的降低。 控制质量明显好于Ziegler-Nichols方法
图2中提出的方法的瞬态有一些脉冲干扰。 它们源于PID控制器的微分部分和受控系统的传输延迟之间的相互用。
III 离散时间PI和PID控制器的最优设置
具有采样周期Delta;t的离散控制信号的自动控制系统的框图如图3所示。
Fig. 3. Discretized automatic control system.
图3中给出的系统的仿真需要分离以不同周期求解的元素。 求和节点以及控制器用周期Delta;t求解。 对于系统的连续部分,受控系统的模型用步骤delta;t解决。 步骤delta;t可以是固定的或可变的。 它取决于所选择的求解描述受控系统的微分方程的方法。
|
SAMPLING RATE IMPACT ON THE TUNING OF PID CONTROLLER PARAMETERS 45 |
- 离散时间控制器的实现
在SIMULINK环境中,上述离散控制系统需要两个ZOH(零阶保持)外推器,它们必须放置在控制器的连续模型之前和之后(图4)。
Fig. 4. Diagram of the discrete control system in SIMULINK.
仿真结果表明,即使原始连续系统稳定并且受控信号的瞬态最优,将ZOH外插器插入连续系统(图4)也会导致系统不稳定。
对于系数N = 20,即使对于时间段Delta;t的小值,也会出现不稳定性。 考虑到采样周期Delta;t,必须选择与图4的系统一起使用的控制器(1)的最佳设置。 通过使用PID控制器的离散形式可以避免这个问题。
上面讨论的离散控制器形式被用在图5所示的控制系统中。
Fig. 5. Diagram of control system with a discrete controller in SIMULINK.
在图5的框图中,控制器方程采用欧拉正向方法[11]获得,该方法给出了应用于(1)的PID控制器公式。 这使得图5中的系统能够对应于图4中的系统。PID控制器的这种形式的公式通常在控制装置中实现[13]: (11)
其中: Sk = Skminus;1 ek.
等式(11)被称为位置算法。 其SIMULINK图如图6所示。来自图6的框图放置在图5的图中的触发子系统PID(z)块内。
- 仿真结果
对于信号采样周期,连续(1)控制器和离散(11)控制器的控制系统的输出(受控)信号的瞬态如图7所示:Delta;t= 0.001。 根据控制系统的时间缩放,采样周期Delta;t与惯性时间常数T有关。
图6.在SIMULINK中定位PID算法图。
图7.连续和离散控制系统的时间曲线
两个控制器的设置由方程(10)计算。受控系统由公式(2)定义,系数theta;= L / T = 0.2。从离散和连续控制系统获得的受控信号的瞬变非常接近(图7)。观察到连续(1)和离散(11)控制器的相似行为对于系数N的相对高的值。如前所述,N的值等于20.系数N的这个值降低过滤对连续控制器(1)的导数分量的影响。
具有PI和PID控制器的控制系统的阶跃响应如图2和图3所示。 8和9进行了模拟。对各种Delta;t值进行了仿真。在每次模拟中,控制器参数设置为连续控制器(1)计算出的最优值。可以看出,尽管选择了最佳参数,Delta;t的增加导致两种控制器的控制质量的损失。 PID控制器对Delta;t的变化更敏感(图9)。
图8.带有PI控制器的控制系统中的受控变量在不同采样周期内时间曲线。
图9.带有PID控制器的不同采样周期的控制系统中的受控变量的时间曲线。
C.采样速率对离散时间PI控制器参数的影响
Nelder-Mead方法被用来寻找PI控制器的最优(3)设置[12]。 PI控制器的最佳参数如图10所示。结果显示控制信号采样周期对控制器质量和控制器参数的影响。可以看出,采样周期Delta;t的增加导致比例增益Kc的最佳值的降低。同时,积分时间Ti的最佳值增加。系统对theta;的小值表现出这种方式。随着系数theta;的增大,Kc的最优值减小并且几乎与采样时间无关。 Ti的最佳值对采样周期更敏感。这意味着对于theta;较小的系统,离散控制器使用连续控制器的最优设置需要改变其两个参数:Kc和Ti。对于theta;较大的系统,只有Ti值应该改变。
图10. P不同的值:theta;系数和采样周期Delta;t对应的PI控制器的最佳参数。
作为控制信号的采样周期Delta;t的函数的ITAE指数最优值在图11中示出。这些值对应于图10中示出的设置。
图11.具有PI控制器的系统的ITAE最优值作为Delta;t的函数。
连续控制系统的特点是ITAE指数最低(图11)。 这个现象发生在theta;的所有值上。 这意味着连续系统提供了最佳的控制质量。 离散控制器的使用只会降低控制的质量。 控制器以周期Delta;t周期性地响应系统信号,因此关于样本之间的控制系统状态的部分信息丢失。 离散控制器根据缺陷数据生成控制信号。 它必然导致控制质量的损失。
具有PI控制器的系统的阶跃响应如图12所示。根据图10选择控制器设置。受控系统theta;= 0.2
|
SAMPLING RATE IMPACT ON THE TUNING OF PID CONTROLLER PARAMETERS 47 |
图12.具有PI控制器的控制系统的受控信号的瞬态与期间Delta;t有关的最佳设置。
图8和12显示过冲减少了,特别是对于采样周期Delta;t较大的系统。 虽然上涨时间的延长会导致控制变量的瞬态变慢。 但是反应时间已经改善
- 采样率对离散时间PID控制器参数的影响
使用Nelder-Mead方法识别最优PID控制器设置。 这些设置作为theta;和Delta;t系数的函数在图13,14和15中。
图13.:Kc,Ti对于不同的值:theta;系数和采样周期Delta;t PID控制器的最佳值。
如图13中theta;的最小值所示,比例增益Kc的最优值随着Delta;t的增加而减小。 同时,积分时间Ti的最优值增加。 微分时间Td的最优值随着Delta;t的增加而减小 - 图14.应该注意的是,对于theta;的小值,Td的变化相对较小。
图14.PID控制器的Kc,Td对应不同的值:theta;系数和采样周期Delta;t。
图15.PID控制器的Td,Ti对应不同的值:theta;系数和采样周期Delta;t。
(图14和15)。 随着theta;的增大,Kc的最优值范围减小,而Ti和Td的最优值变化范围增大。
这意味着对于theta;较小的系统,离散控制器的连续控制器的最佳设置的使用需要Kc的显着变化,Ti的微小变化以及Td的几乎没有变化。 对于theta;较大的系统:必须改变Ti和Td,而Kc可能保持几乎不变。 关于PI控制器,使用PID控制器的控制系统对比例增益Kc更敏感(图10和13)。
具有PID控制器的系统的ITAE指数最优值作为受控信号采样周期的函数如图16所示。
就像带有PI控制器的系统一样,对于带有PID控制器的连续控制系统,可以观察到最佳的控制质量。 离散控制器的使用只会降低控制质量。 PID控制器的使用提高了控制质量,特别是对于theta;值较大的系统(图11和图16)。
图16.具有PID控制器的系统的ITAE最优值与Delta;t的函数关系。
图17.具有PID控制器的控制系统的阶跃响应,用于与时间段Delta;t有关的最佳设置。
具有PID控制器的系统的最佳阶跃响应在图17中示出。与这些值相对应的控制器设置在图17和19中示出。 13和14比较图。 从图9和图17可以看出,控制质量显着提高,特别是对于采样周期较大的系统。 超调减少,建立时间缩短。
IV。 结论 全文共7157字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[16022],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


