
英语原文共 8 页
摘 要
图像去噪是低水平视觉中一个经典但基本的问题,也是评估各种统计图像建模方法的理想测试平台。图像去噪中最具挑战性的问题之一是如何在去除噪声的同时保持精细尺度的纹理结构。
各种自然图像先验,例如基于梯度的先验、非局部自相似先验和稀疏先验,已经被广泛用于图像去噪中。然而,基于这些先验的去噪算法倾向于平滑掉详细的图像纹理,降低了图像的视觉质量。为了解决这个问题,在这篇论文中,我们提出一种纹理增强图像去噪( TEID )方法,通过迫使去噪图像的梯度分布接近原始图像的估计梯度分布来达到这个目的。
为了在去除噪声的同时增强纹理结构,我们提出了一种新的梯度直方图保持算法。实验结果表明,我们所提出的基于GHP的TEID能够很好地保留去噪图像的纹理特征,使去噪图像看起来更加自然。
1.简介
图像去噪的目的是从其噪声观测值y估计潜在的干净图像x。一种常用的观测模型如下式所示:
y = x v
其中v是加性高斯白噪声。
图像去噪是图像处理和低水平视觉领域中一个经典但仍然活跃的课题,同时也是评估各种统计图像建模方法的理想测试平台。一般来说,我们希望去噪后的图像看起来像自然图像,因此自然图像先验的统计建模对于图像去噪的成功至关重要。
基于自然图像梯度呈现重尾分布的事实,基于梯度的先验被广泛用于图像去噪。众所周知的总变化差最小化方法实际上假设图像梯度为拉普拉斯分布。通过观察,自然图像可以在冗余的dic-上进行系数编码。
通过l0范数或l1范数最小化,稀疏先验在图像去噪中被证明是有效的。另一个流行的先验是非局部自相似性( NSS );也就是说,在自然图像中,通常存在许多与给定图像块相似的图像块(即,非局部邻居),这些图像块在空间上可能远离所给定图像块。稀疏先验和NSS先验的联合使用导致了最先进的图像去噪结果。然而,许多基于上述先验的去噪算法仍然不能保持图像的精细尺度纹理结构,这些纹理结构在频域中与噪声有一定的重叠。这些细节纹理结构的过度平滑使得去噪后的图像看起来不太自然,大大降低了视觉质量(例如,请参考图1 )。
随着数字成像技术的快速发展,成像传感器的分辨率越来越高。一方面,将捕获对象和场景的更精细纹理特征;另一方面,因为每个像素的较小尺寸使得曝光不够充分,加盖的高分辨率图像更容易受到噪声的影响。然而,在保持纹理的同时抑制噪声很难同时实现,这也是目前自然图像去噪中最具挑战性的问题之一。与大尺度边缘不同,细尺度纹理在局部结构中具有更高的随机性,并且它们很难通过使用局部模型来表征。考虑到图像中的纹理区域是同质的,通常由相似的图案组成,统计描述符(如直方图)更能有效地表示它们。实际上,在纹理表示和分类的文献中,一些局部特征的全局直方图主要用作匹配的最终特征描述符。同时,图像梯度传达了图像中的大部分语义信息,并且对人类对图像视觉质量的感知至关重要。所有这些促使我们使用图像梯度直方图来设计新的图像去噪模型。
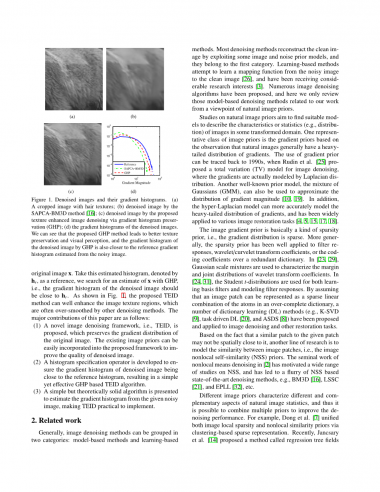
图1 去噪图像及其梯度直方图。
(a)带有头发纹理的裁剪图像;(b)采用SAPCA-BM3D方法对图像进行去噪;
(c)利用梯度直方图保持的纹理增强图像去噪;(d)去噪图像的梯度直方图。
如图1所示可以看出,所提出的GHP方法具有更好的纹理保存和视觉感知能力,经过GHP去噪后的图像的梯度直方图也更接近由噪声图像估计的参考梯度直方图。
基于以上考虑,本文提出了一种基于梯度直方图保持的纹理增强图像去噪方法。根据给定的噪声图像y,我们将估计的梯度直方图原始图像x,以hr表示的估计直方图为参考,通过GHP对x的估计进行处理,使得去噪后图像的梯度直方图应接近hr。如图1所示,所提出的TEID方法能够很好的增强图像的纹理区域,这些区域往往会被其他去噪方法过度平滑。本文的主要贡献如下:
(1)一种新颖的图像去噪框架,即保留了原始图像的梯度分布。现有的图像先验可以很容易地纳入该框架,以提高去噪图像的质量。
(2)为了保证去噪图像的梯度直方图接近参考直方图,提出了一种简单而有效的基于GHP的TEID算法。
(3)提出了一种简单但理论上可靠的算法,可以从给定的噪声图像中估计梯度直方图,使TEID具有实用性。
2.相关工作
一般将图像去噪方法分为两大类:基于模型的方法和基于学习的方法。大多数去噪方法都是利用已有的图像和噪声模型对图像进行重构,属于第一类去噪方法。基于学习的方法试图学习从噪声图像到干净图像的映射函数,并得到了相当大的研究兴趣。众多的图像去噪算法已经被提出,这里我们仅从自然图像先验的角度来回顾与我们工作相关的基于模型的去噪方法。
自然图像先验研究的目的是寻找合适的模型来描述某些变换域图像的特征或统计量(如分布)。梯度先验是一类典型的图像先验,它基于对自然图像中梯度分布的粗尾观察。梯度先验的使用可以追溯到20世纪90年代,当时Rudin等人提出了一种用于图像去噪的全变分(TV)模型,其中的梯度实际上是用拉普拉斯分布来建模的。另一个著名的先验模型高斯混合模型(GMM)也可以用来近似梯度幅值的分布。此外,hyper-Laplacian模型能够更准确地模拟梯度的重尾分布,已广泛应用于各种图像恢复任务。
图像梯度先验基本上是一种稀疏先验,即,梯度分布是稀疏的。通常,稀疏先验已经很好地应用于滤波响应、小波/曲线变换系数或冗余字典上的编码系数。在[23,29]中,采用高斯尺度混合来表征小波变换系数的边缘和联合分布。在[24,31]中,学生t分布用于学习基础滤波器和建模滤波器响应。通过假设图像patch可以表示为过完备字典中原子的稀疏线性组合,提出了多种字典学习(dictionary learning, DL)方法(如K-SVD[9]、task driven DL[20]、ASDS[8]),并应用于图像去噪等恢复任务。
基于与给定图像块相似的块可能在空间上并不接近它这一事实,另一个研究方向是对图像块之间的相似性进行建模,即图像非局部自相似性( NSS )先验。非局部均值去噪的开创性工作激发了国内外众多学者对NSS的广泛研究,并导致了一系列基于NSS的最新去噪方法,例如BM3D [16], LSSC[21]和EPLL [32]等等。图像先验特征可能描述图像的不同方面,也有可能描述自然图像互补方面的统计数据,因此它可以组合多种先验改善去噪性能。例如,Dong等人通过基于聚类的稀疏表示,统一了图像的局部稀疏性和非局部相似性先验。最近,Jancsaryet 等人[14]提出了一种称为回归树域(regression tree fields, RTF)的方法来集成不同的先验。
然而,现有的许多图像去噪算法,包括稀疏性算法和基于NSS先验的去噪算法,往往在去除噪声的同时去除图像的细节纹理。
如前文所述,考虑到图像纹理区域的随机性和同质性,我们提出利用梯度直方图来描述图像纹理,设计一种新的梯度直方图保留的图像去噪算法。Cho等人利用超拉普拉斯分布对梯度进行建模,通过设置不同图像区域梯度分布的形状参数,提出了一种图像去模糊的内容感知先验。另外,Cho等人通过对梯度分布先验的匹配,发现去模糊后的图像可以拥有更详细的纹理以及更好的视觉质量。然而,在[4,5]中,期望梯度分布的估计具有很强的启发式,梯度直方图匹配算法非常复杂。
3.梯度直方图保持去噪(GHP)
在这一节中,我们首先提出了一种基于稀疏非局部正则化的梯度直方图保留图像去噪模型,然后给出了一种有效的直方图规范算法来解决纹理增强图像去噪问题。
3.1去噪模型
对于干净的图像x,噪声观测y (x)通常建模为
y = x v, (1)
v是加性高斯白噪声(AWGN),其均值为0和标准差表示为sigma;。图像去噪的目标是估计出所需的图像的x坐标。一种常用的图像去噪方法是变分方法,该方法可以表示为以下式子:
R(x)表示一些正则化项,其中参数micro;是正的常数。R(x)的具体形式取决于使用的图像先验。
图像去噪的一个常见问题是纹理结构等精细尺度的细节会被过度平滑。过度平滑的图像会比原始图像有更弱的梯度。直观地说,在不过度平滑纹理的情况下,对x的良好估计应该具有与x相似的梯度分布。基于这种动机,我们提出了一种用于纹理增强图像去噪(TEID)的梯度直方图保留(gradient histogram preservation, GHP)模型。
我们直观的想法是将梯度直方图先验与其他图像先验相结合,进一步提高去噪性能。假设我们估计了x的梯度直方图,用hr表示,(估计方法将在第4节讨论)。为了使去噪后的图像x的梯度直方图与参考直方图hr接近,我们提出了以下基于GHP的图像去噪模型:
F表示一个奇函数是单调非递减函数,取值(0, infin;)。hF表示转换后的梯度图像的直方图| F(nabla;x)|,nabla;表示梯度算子。通过引入变换F,我们可以采用交替的方法进行图像去噪。至于F,我们可以解决nabla;x0 = F(nabla;x)和使用传统的去噪方法更新x。
给定x,我们可以通过3.2节中介绍的直方图操作符来更新F。因此,通过引入F,我们可以很容易地将梯度直方图先验与任何现有的图像先验R(x)结合起来。
稀疏性和NSS先验在去噪方面表现出了良好的性能,因此我们将它们集成到所提出的GHP模型中。具体来说,我们采用了集中式稀疏表示(CSR)模型[7]中提出的稀疏非局部正则化项,从而得到了以下去噪模型:
其中正则化参数lambda;,D是字典和alpha;是编码系数x / D。
让我们进一步解释式(3)中的模型,假设xi =Rix是在位置i, i = 1,2,hellip;N,其中Ri为patch提取算子,N为图像中像素的个数。每个xi都在字典D上编码,编码系数是alpha;i。让alpha;代替所有的alpha;i,然后x可以由以下式子重构:
式(4)的物理意义是我们使用^xi =Dalpha;i重建每个贴片xi,然后将所有重建的贴片放在一起重构为去噪图像(相邻贴片之间的重叠像素被平均),
在式(3)中,beta;i是稀疏编码域中alpha;i的非局部均值。利用当前估计x,我们使用[7]中的阻塞匹配方法来找到x i的非局部邻居,用x qi表示,用alpha;qi表示x qi的编码系数。 那么beta;i被计算为alpha;qi的加权平均值,其中h是控制衰减速率的参数,W是保证的归一化因子。显然,正则项强制编码系数alpha;i接近其非局部均值beta;I,从而可以去除噪声,而L -范数来自遵循拉普拉斯分布[ 7 ]。
从具有稀疏非局部正则化的GHP模型(3)可以看出,如果直方图正则化参数mu;高,则函数F(nabla;x)将接近nabla;x。由于| F(nabla;x)|的直方图hF 需要与hr相同,nabla;x的直方图将类似于hr,导致所需的梯度直方图保留图像去噪。
接下来,我们将看到有一个有效的迭代直方图规范算法来解决模型(3)。
3.2迭代直方图规范算法
式(3)需要被迭代最小化。如[7]中所述,局部PCA基被用作字典D.基于图像x的当前估计,我们将其图像块聚类为K个聚类,并且对于每个聚类,学习PCA字典。 然后,对于每个给定的块,我们首先检查它所属的集群,然后使用该集群的PCA字典作为D.
我们提出了一种交替最小化方法来解决(3)中的问题。 给定变换函数F,我们引入变量g = F(nabla;x),并通过解决以下子问题来更新x(即alpha;):
为了解决上述子问题,我们首先使用梯度下降方法来更新x,最后,我们总结了算法1中提出的基于迭代直方图规范的GHP算法。应该注意的是,对于任何基于梯度的图像去噪模型,我们可以通过简单地修改梯度项并添加额外的直方图规范操作来容易地将提议的GHP结合到其中。
4.实验结果
我们首先给出了基于GHP的TEID算法中的参数设置,然后进行实验验证它与最先进的去噪算法相比的性能。最后,我们对其潜在的改进进行了一些讨论。
4.1参数设置
我们的算法需要设置一些参数,如等式( 7 )中的正则化参数lambda;和mu;是用来平衡梯度保持的效果,等式( 8 )中的常数delta;和等式( 10 )中的d目的是确保凸面。对于参数lambda;,我们使用与[ 8 ]相同的最大后验( MAP )原理的策略自适应更新它。根据我们的实验经验 ,对于小于30的噪声水平,我们将参数mu;设置为5,我们将delta;设置为0.23,而对于其他噪声水平,将delta;设置为0.26。基于[ 6 ]中的分析,为了保证替代函数的凸性,d应该大于字典D的谱范数。因为在我们的算法D是正交PCA矩阵,任何大于1的d都是好的,我们根据经验将其设置为3。请注意,在我们的实验中,这些参数固定在所有图像上。
4.2去噪结果
为了验证我们提出的基于GHP的TEID方法的性能,我们将其应用于10幅具有不同纹理结构的自然图像。这些图像的场景可以在图3中找到。一些最先进的去噪方法被用于比较,包括基于形状自适应PCA的BM3D ( SAPC - BM3D ) [ 16,同时学习的稀疏编码( LSSC) [21]和CSR [7]方法。所有竞争方法的代码由作者提供,我们使用了作者推荐的参数。考虑到当噪声太强时,所有方法都无法恢复图像中的精细尺度纹理结构,实际上噪声通常是中等或低的,我们在实验中设置AWGN噪声水平sigma;isin;{ 20,25,30,35,40 }。
竞争方法的定量实验结果如表1所示。除了PSNR,我们还使用感知质量度量SSIM [30列出了结果。从该表中,我们可以看出,所提出的GHP方法与SAPCA - BM3D、LSSC和CSR具有相似的PSNR/SSIM度量。尽管如此,我们GHP方法的目标是保持和增强图像纹理结构,让我们比较这些方法去噪后图像的视觉质量。图4示出了一个例子。在这张图像中,有不同的纹理区域,例如天空、树、水和建筑。我们可以看到SAPCA-BM3D、LSSC和CSR平滑了树木、水和建筑
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


