
英语原文共 13 页,剩余内容已隐藏,支付完成后下载完整资料
摘要
这项研究的主要目的是开发一种新型的高性能轻型梁,通过将纤维增强聚合物(FRP)增强钢筋添加到超高性能混凝土与超细纤维增强材料(UHPC-SFR)中,改善传统钢筋混凝土(RC)的性能。这种新型梁的设计重量轻,具有很高的抗压和抗拉强度,能够承受较大的弯矩,并且能够抵抗剪切作用。主要目标是验证梁的力学行为并将其与典型RC梁的行为进行比较。设计了一个实验程序来识别其失效模式和弯曲行为。结果表明,这种RC梁的行为在一定程度上与典型的RC梁特性相当。这里给出一个验证这个概念的分析模型,它是基于典型的非线性机械梁行为的材料行为定律假设。使用此模型预测的载荷位移和力矩曲率关系与几个大型标本的实验结果进行了比较。这些比较揭示了分析和实验结果之间的良好相关性,并说明了这些组合梁在土木工程结构中的潜力。
1、简介
高性能材料在土木工程领域的应用研究和开发近年来在欧洲和全球取得了显着进展,其中包括超高性能微纤维混凝土(UHPC-SFR)和纤维增强聚合物(FRP)。 UHPC-SFR在压缩和张力两方面都很强,并且由于其低渗透性可以有助于缓解环境暴露的影响。因此,预计这种材料的使用将会增加,特别是在考虑可持续发展原则时[1]。此外,使用UHPC可以使设计师创造更薄的部分和更长的跨度,在几何和形状方面都是轻量级,优雅和创新的,具有低渗透性和良好的耐腐蚀性,耐磨性和耐冲击性[2]。可以消除剪切箍筋,从而增强安全性,减轻重量并允许更快建造。此外,其耐久性降低了维护要求并延长了使用寿命。所有这些因素都有助于降低成本[3]。 最后,在全球范围内,UHPC在建筑中的使用已经显着增加,因此现在有必要使用优化其使用的新方法[4,5]。
最近,使用纤维增强聚合物(FRP)钢筋取代钢筋已成为提高钢筋混凝土结构抗腐蚀性的众多技术之一。 它已被用于加固和修复新建筑。 特别是,在常规钢筋混凝土表现出不可接受的性能的条件下,FRP钢筋提供了用于钢筋混凝土施工的巨大潜力[6,7]。
在新兴建筑领域,对使用玻璃钢材料和其他高性能材料的混合结构构件进行研究以产生新的结构优势显着增加[7,8]。 这些新设计的混合动力构件的目标是提高全球结构性能和耐腐蚀性,而且与传统钢结构相比,还可以节省成本。一项关于在威斯康星州建造FRP钢筋混凝土桥面板的研究表明,与建造名义相同的钢筋面板相比,其比传统施工技术和普通强度混凝土可节省57%的建筑劳动力成本[9]。
此外,许多研究集中在嵌入混凝土中的FRP钢筋的粘结滑移行为,以防止出现意外剥离[10-15]。已经表明,增加的混凝土强度对应于增加的FRP钢筋强度[16]。 UHPC的使用可以使FRP钢筋的全面复合作用得以开发。 UHPC-SFR和FRP钢筋之间的粘结行为在本研究中尚未发展,尽管这种性质代表了将这两种高性能材料结合起来的另一个好处。
在这里,我们提出了一个由UHPC-SFR构成并用碳纤维增强聚合物(CFRP)增强的新型RC梁的研究的实验结果。
为了最大限度地减少UHPC的用量并改善抗压强度的充分利用,提出了梁的特定横截面。 当UHPC与FRP钢筋相关时,它可能在失效时产生较高的拉伸应力。 两种高性能材料的组合提高了故障时的材料应力水平。 第一个横截面是UHPC中空部分,旨在避免剪切失效。 第二种配置设计为仅在强度至关重要的区域包括UHPC,例如顶部和底部的压缩和抗拉强度。 一层UHPC铸造在几厘米的下梁和上梁部分。 在这之间,使用标准的C25混凝土。
实验测试是在2米和4米跨度的梁上进行的,为此展示了这种创新型钢筋混凝土结构的高性能。 考虑了三种类型的部分。 目标是开发不同的失效模式。 为了实现这一目标,该部分的几何结构适用于每个案例研究。 我们试图避免玻璃钢增强材料的拉伸破坏。
2纤维增强聚合物-超高性能微纤维混凝土梁的设计
2.1 材料
2.1.1 超高性能微纤维混凝土
使用的超高性能混凝土是Ductalreg;G2预混料。为了评估其机械性能,对每批混凝土进行了机械测试。这些横梁分四批投射。对六块UHPC棱镜进行四点弯曲试验以测量它们的弹性模量Ec和弯曲强度(表1)。根据JSCE的UHPC标准[17],六个圆柱形混凝土试样在铸造后28天进行压缩试验。 获得了171plusmn;1.8MPa的平均抗压强度。
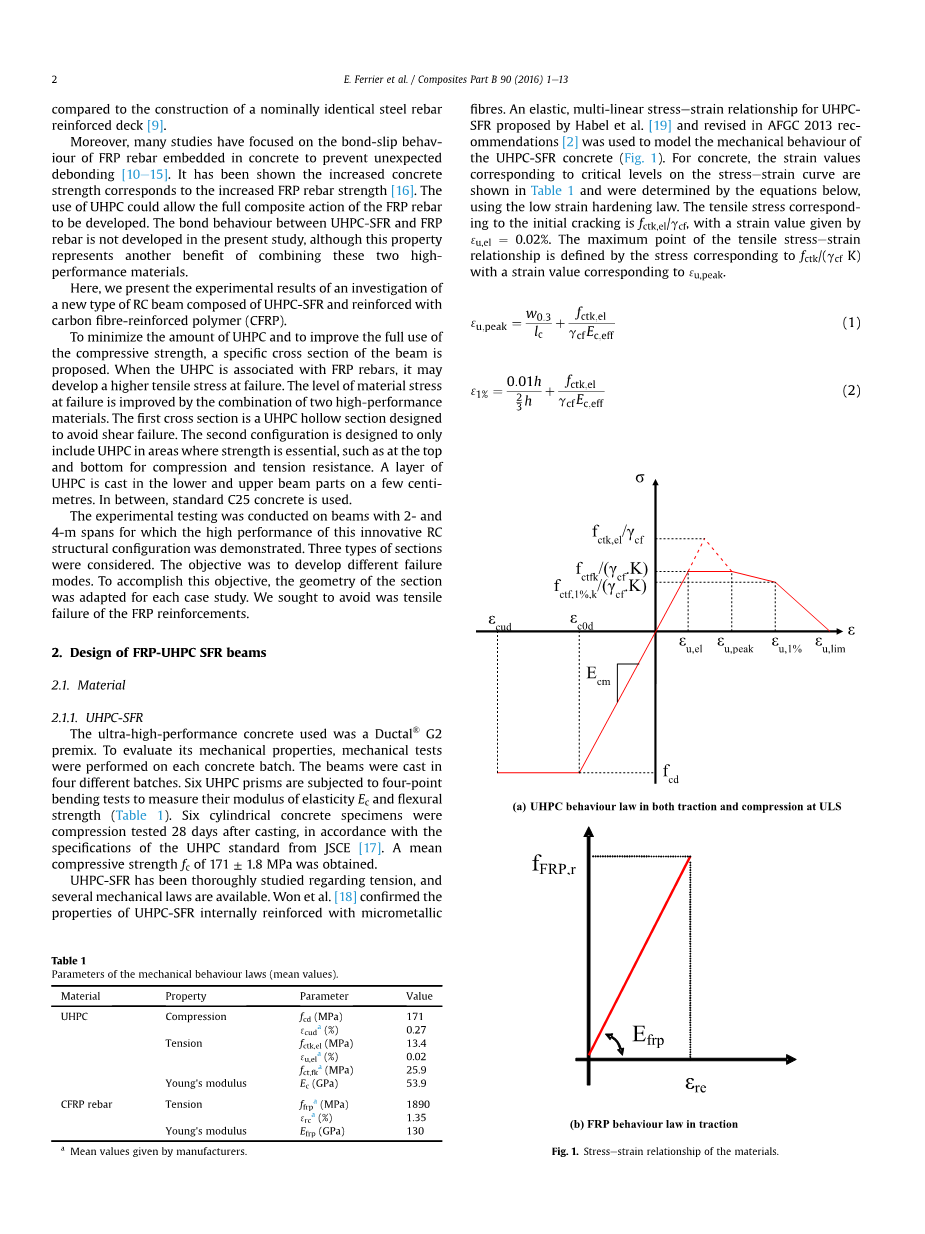
超高性能微纤维混凝土已被彻底研究过张力,并且有几种机械法则可供使用。 Won等人[18]证实了用微金属纤维内部增强的UHPC-SFR的性能。 Habel等人提出的UHPC-SFR的弹性,多线性应变关系,[19]并在2013年AFGC修订建议[2]被用来模拟UHPC-SFR混凝土的力学行为(图1)。 对于混凝土来说,相应于应力应变曲线上临界水平的应变值。 拉伸应力关系的最大点由与 /( K)对应的应力定义,其应变值对应于。
(1)
(2)
(3)
图1 材料应力-应变关系图
在这些方程中,h是截面的深度是特征弹性拉伸强度,是特征最大开裂应力,是UHPC的有效弹性模量。是等于2h / 3的特征长度,是纤维的长度。是纤维的部分安全系数。当拉伸区中的较高部分应变达到的值时,假定UHPC中的拉伸发生失效。 当混凝土应变大于时,拉应力等于零。
这个假设可以用于由微金属纤维内部加固的混凝土的开裂行为[2]。对于混凝土受压情况,ULS,的最大压缩应变可以等于,这是AFGC [2]初步设计推荐的值。
2.1.2 通常的混凝土
在由三层混凝土制成的梁的情况下,在最小应力区域中使用25MPa的标准混凝土抗压强度,该区域是两层UHPC之间的部分的中心部分。这种混凝土是根据Dreux-Gorisse的方法制造的,0.6的比值W / C由Bolomey公式确定。使用标准的波特兰水泥,砂石和砾石颗粒材料为轧制类型。粒度分析显示沙子为0/4级颗粒类型,砾石为5/10级。该混凝土是在LYON 1大学的实验室中生产的。混凝土强度达到25MPa的配合比如表2所示。
对于每批,根据NF EN 12390-1标准铸造三个对照样品(圆柱160times;320mm)。然后根据NF EN 12390-4对照样品进行压缩测试以确定每种混凝土的抗压强度。获得的平均抗压强度为25.2MPa。没有进行用于确定杨氏模量的拉伸测试和测量。计算中考虑了EC2 [20]的值。
2.1.3 FRP螺纹钢
实验室没有测试FRP钢筋的材料属性。 相反,供应商提供的财产价值被用于计算。 所用的CFRP钢筋是用浸渍在乙烯基酯树脂中的连续碳纤维制成的。 表面是螺旋状包裹和沙涂层。 表1给出了钢筋的其他力学性能(拉伸强度ffu和Ef杨氏模量),梁的几何形状和钢筋比率总结在表3中。
2.2 部分描述
第一部分是典型的钢筋混凝土梁,其带有纵向和横向钢筋。
第二部分配置的目标是减少梁的重量。 两个塑料空心管放置在这些部分中,使得混凝土的最小垂直层不与沿该部分高度的最大剪切应力相匹配。
由于混凝土中的拉应力很高,因此将UHPC-SFR浇注到置于胶合板模具中的中空管周围的所有部分中。 三种FRP混凝土复合材料梁采用不同尺寸的中空塑料管浇铸而成, 其截面高度和宽度见表3.表3给出了这三种梁的详细材料和几何特性。
第三个配置部分的目标是降低使用UHPC-SFR和FRP钢筋组成的混合梁的成本。 UHPC-SFR仅浇注在梁的底部和顶部,其中拉伸应力和压缩应力最高。 在这两层之间,浇注普通强度的混凝土。 在类型2(图2)的情况下,用FRP加固的梁中UHPC底层的厚度表示为hf2。 梁中UHPC顶层的厚度用hf1表示。 实验中,UHPC-SFR层在普通强度混凝土的同一天浇注,因此两种混凝土之间的界面由新鲜至新鲜浇注而产生。设计了两种类型的梁2,其特征也在表4中报告。
选择了几个参数来评估梁的效率。 几何和材料参数,如梁的深度和跨度,深宽比,混凝土与微型钢纤维的体积百分比,抗拉钢筋与钢筋的机械性能(包括轴向刚度)的体积比以及机械强度 混凝土和FRP的性能都很重要。 在这项研究中,所研究的参数是梁跨度,深宽比以及下部钢筋的抗拉强度(图2)。 两片梁是相同的,只是一根梁具有2%的微金属纤维体积百分比,而第二片具有1%的体积百分比。
为了在CFRP钢筋中发挥尽可能高的强度,UHPC-SFR作为钢筋周围的混凝土浇注在梁的底部,如图2所示。该组合允许底部的整体抗拉强度 RC梁增加。 首先设计参考梁来比较这里研究的新混合梁的性能。 然后,选择两个部分配置。
设计的梁宽150毫米,高250毫米。 两根15毫米直径CFRP的钢筋总是加固比较梁的截面。 该梁设计为包含UHPC的顶部3cm层和包裹FRP增强件的低于6cm的UHPC层。
为了比较标准溶液和夹层梁,每种材料的密度总结在表5中。然后计算每种成分的重量,结果如表6所示。
这两种解决方案的梁重量是相等的,所以夹层梁的配置没有重量增加。 然而,相对于全UHPC梁或空心梁而言,存在UHPC经济。
表7中总结了上述每个2m梁的UHPC数量。
相对于片梁而言,UHPC对于铸造梁不那么重要。 然而,从经济学的角度来看,传统混凝土的成本应该在考虑前者时加上,而后者则是空的。 可以计算出成本最高的部分。 另外,不同混凝土层之间的粘结问题可能发生在多层梁中,而中空梁是整体式的。
图2 材料应力-应变关系图
2.3 剪切设计
2.3.1 空心梁
使用Autodesk Robot Structural Analysis软件对两部分进行评估,以确定测试梁的最终配置。第一部分(图3)由一个直径200毫米的空心圆柱体组成。 为了评估排列和孔的数量的影响,第二种结构(图3)包含两个100mm直径孔的中空部分。第一部分具有122.7cm 2真空表面,而第二部分对应于157cm 2。这些值报告在表8中。第二部分进一步降低梁截面的剪应力。此外,在两个孔的情况下,达到的最大剪切应力除以两个以上。关于预期的最大剪应力,使用UHPC是合理的。因此,优选在实验设计的凹陷部分中包含两个而不是一个圆柱体。
图3 空心梁结构(a)和三层梁结构(b)的最大剪应力
2.3.2 多层梁
如上所述,多层梁具有顶部3厘米的UHPC层,然后是典型混凝土(C25)和6厘米底层的中间层。设计中忽略了顶部和底部的剪切强度。梁由8毫米直径的横向箍筋加固,每150毫米放置一块箍筋。欧洲规范2标准提供梁的抗剪强度计算如方程式(4)。
(4)
剪切破坏载荷计算如方程式(5)。
(5)
方程(6)给出混凝土强度贡献;钢的贡献按照公式(6)计算。
(6)
(7)
是横向箍筋区域,s是箍筋之间的间距,是钢筋强度,z取0.9d。箍筋贡献是64kN。最后,计算出的抗剪强度为86.6 kN,总破坏载荷为173 kN。
2.4 中空梁和多层梁的弯曲设计
计算梁的弯曲能力。对于弯曲强度来说,混凝土的压缩是有限的,并且假定混凝土发生破坏时的变形达到0.0027m / m。计算使用增量迭代计算进行。由于截面的几何性质,UHPC的非线性行为和多层截面的使用,中性轴深度是未知的。计算合成压缩力的过程如图4所示。梁深度沿其高度被分成1000层。 首先,假定,并且计算应力分布。然后,将混凝土的力学行为规律简化为双线性规律,并且知道钢筋的本构规律,计算出与假定应变相对应的每一层的应力。
通过公式表达每层的合成压缩力,如方程式(8)
(8)
(9)
基于截面平衡,压缩力和拉伸力相等,从而允许计算中性轴位置。
(10)
其中:
(11)
积分是使用辛普森近似离散计算的。在数值分析中,以托马斯辛普森命名的辛普森方法是一种用于获得有限域上函数积分结果的方法。所得结果一般容易近似。在我们的例子中,取决于圆的方程,并随梁深度的变化而变化。目标是获得方程式给出的积分值,具体每一步都由时(5)给出。
(12)
该方法利用函数的二阶近似使用多项式方程,其对于每个,和m取相同的值,其中m由式(13)给出。
(13)
式(7)就可以被计算出来
(14)
然后整合这个功能变得很容易,如式(15)所示。
(15)
由于UHPC具有相当大的拉伸强度,所以拉力的计算考虑了UHPC的贡献。 所用的相同积分模型是用于压缩力的。 由于FRP的破坏应变极限,UHPC计算中考虑的最大应变为1%。 对于每个应变水平和计算的每一层,应力都是基于UHPC的拉伸力学行为来考虑的。 解决该系统产生近似值xf。 然后使用方程式计算内部力矩,如式(16)所示。
(16)
这些梁在四点弯曲中进行了测试,因此使用方程式(17)计算了弯曲过程中的失效力。
全文共14010字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[14741],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


