
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
208 6章
-
- 设计强度在弯曲的紧凑形状
示例6-1
W 形状的分类
确定 的 分类 的 a W18 times; 35 和 a W21 times; 48 为 Fy = 50 ksi. 检查法兰和 Web。
从1部分的AISCM,
W18 times; 35 W21times; 48
bf bf
= 7.06 9.47
2tf 2tf =
H = 53。5 h 53。6
tw tw =
hpf=0.38一个F = 0.38A 50 =9.157 7.06;
法兰:
E 2.9万
h射频=1。0一个F = 1。0A 50 =24。079.477 9.15;
y
lsaquo; W18*35法兰是紧凑的。
E 2.9万
y
lsaquo;W21*48法兰为一类非紧。
h星期五=3.76一个F = 3.76A 50 =90。57 53.6;
Web:
E 2.9万
y
lsaquo;W18*35和 W21*48网是紧凑的。
注意 那 形状 那 是 一类非紧 为 弯曲 是 指出 的 标 f 在 部分 1 对该 AISCM.
基本设计强度方程梁在弯曲是
其中
Mu =计算力矩,
=0.9,
Mn =名义上的弯曲强度
=设计弯曲强度。
公称弯曲强度Mn是以下函数的函数:
-
-
- Lateral–torsional 屈曲(LTB),
- 法兰局部屈曲(FLB), 和
- Web局部屈曲 (WLB)。
-
Noncomposite梁 209
法兰局部屈曲和腹板局部屈曲是局部失效模式,只涉及具有非紧凑型腹板或法兰的形状,后面将详细讨论。
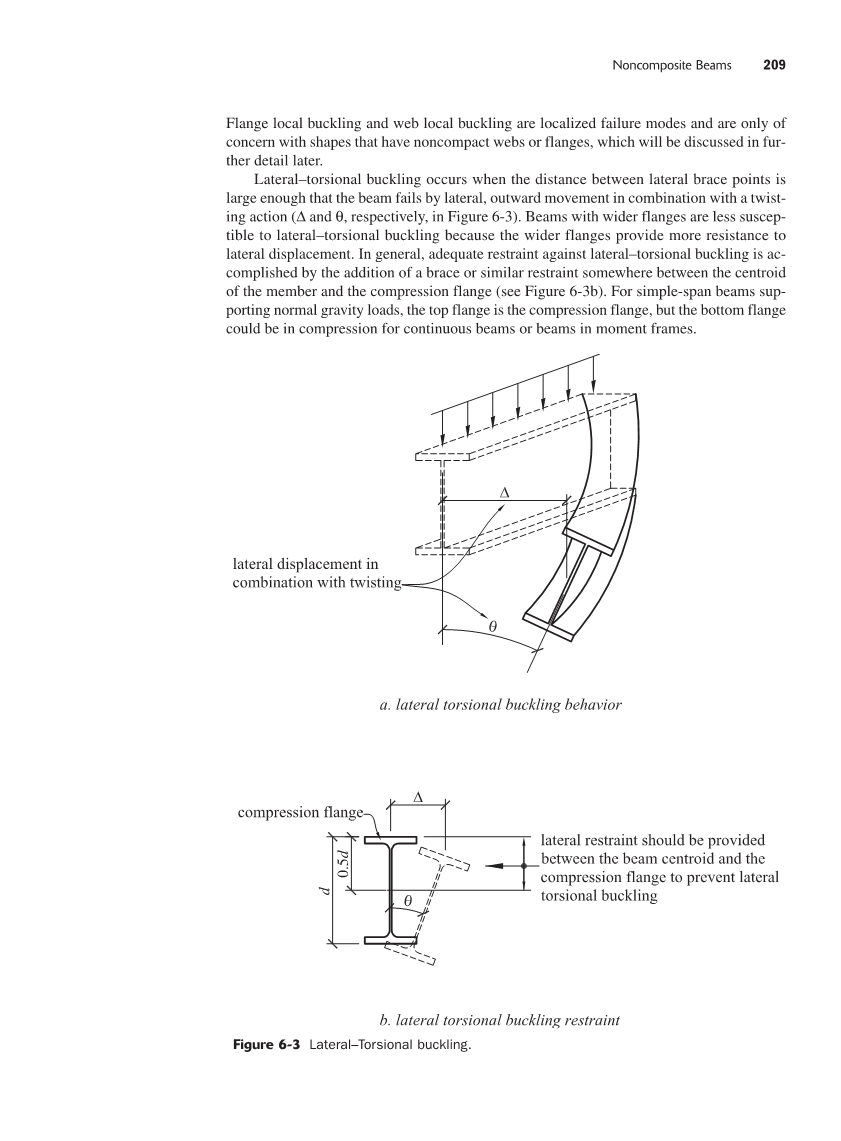
Lateral-torsional屈曲发生在横撑点之间的距离足够大,横向梁失败,向外运动结合扭转操作(Delta;andtheta;,分别在图6 - 3)。法兰较宽的梁不易受横向扭转屈曲的影响,因为法兰较宽的梁对横向位移的阻力较大。一般来说,通过在构件的质心和受压法兰之间添加支撑或类似的约束,就可以充分抑制横向扭转屈曲(见图6-3b)。对于支持正常重力载荷的单跨梁,上翼缘是受压凸缘,但底部法兰可以在瞬间框架内对连续梁或梁进行压缩。
横向位移结合扭转
a.侧扭屈曲
抗压边缘
在梁质心和压缩法兰之间应该提供横向约束,以防止横向扭转屈曲
0.5d
d
图6 - 3 Lateral-Torsional屈曲。
210 6章
侧扭屈曲可以通过多种方式控制,但通常取决于实际的施工细节。与梁跨垂直的金属甲板梁被认为是完全支撑的(图6-4a),而图6-4b中的梁不被甲板认为是支撑的,因为甲板几乎没有刚度来防止梁的横向位移。图6-4c中的梁将被中间框架构件视为支撑,并具有未支撑的长度Lb。
(Lb =0)
b
c
Lb1 Lb2 Lb3
图6-4 侧向支撑细节。
Lb
P
Noncomposite 梁 211
当梁提供了完整的横向稳定性,名义时刻强度是塑料的能力梁(Mp FyZx见1 - 6节)。一旦放松长度达到一定上限,lateral-torsional会发生屈曲,因此同样名义弯曲强度会降低。lateral-torsional屈曲的失效模式可以是弹性或弹性。美国国际留学中心向规范定义了非弹性的放松长度lateral-torsional屈曲发生
(6-5)
Lp也是额定弯曲强度等于塑性力矩能力的最大无支撑长度。弹性横扭屈曲发生的无支撑长度为
(6-6)
其中
(对于通道形状)
E=弹性模量
J=扭转不断
Sx =截面模数 (x 轴),
Iy =惯性力矩 (y 轴),
Cw =翘曲常数
ho =法兰质心之间的距离。
当侧扭屈曲不存在时(即当无支撑长度为Lble;Lp)时,失效模式为弯曲屈服。弯曲屈服的名义弯曲强度为
(6-9)
Fy =屈服强度
Zx =塑性截面模数 (从1部分AISCM)
对于紧凑型i型和c型,当Lp Lb Lr时,名义抗弯强度为 (
212 6章
在 的 以上 方程 的 术语 0。7Fy Sx 是 也 述 自 作为 Mr, 的 对应 自 的限制 屈曲 时刻 当 Lb = Lr 和 是 的 过渡 点 之间 弹 塑性 和 elas-tic lateral–torsional 屈曲 (参见位置Mr 在图 6-5)。
对于紧凑型 I 形形状和 C 形, 当Lb gt;Lr, 公称弯曲强度为
弯曲 和 (6-14)
IYc =压缩法兰的惯性力矩关于y轴.
为 双 对称 形状 IYc 是 大约 平等 自 Iy/2。 为 反曲率弯曲,IYc 是小的惯性力矩 法兰。
的 时刻 梯度 因素 Cb, 帐户 为 的 可能性 那 的 整个 梁 将 不是主题向该最大力矩为该整个长度对该lateral–torsional 屈曲时的光束 控制。 它 是 保守 自 假设 那 Cb = 1。0 为 任何 加载 条件 这意味着 那 的 应用 时刻 是 不断 在 的 整个 梁。 在 代替 的 方程 (6-13)、值 的 Cb 可以 也 是 获得 从 表 6-3, 的 是 基于 上 方程 (6-13)。
的 变化 在 弯曲 强度 与 尊重 自 的 无支撑 长度 是 显示 在 图ure 6-5, 的 总结 的 前 讨论 的 弯曲 强度 为 梁。 这 图显示的弯曲强度为两个紧凑和一类非紧形状。的一类非紧的弯曲强度 形状 将 是 讨论 在 a 后 部分 但 是 表明 这里 为 完整性。
有 是 三 不同 区 显示 在 的 图 的 第一 被 地方 lateral–torsional 屈曲不发生弯曲强度是一个常数值Mp.的第二个和第三个区域显示如何的弯曲强度减小由于 自弹 塑性和弹性lateral–torsional屈曲为无支撑长度 增加。
弯曲强度开始减小的曲线上的点 (即, 当无支撑长度时,Lb等于Lp) 用一个变暗的圆圈表示。弯曲强度经历从非弹性到弹性 lateral–torsional 屈曲的过渡的点 (即当无支撑长度时,Lb等于Lr 当公称弯曲强度时,Mn等于Mr)用一个开放圆圈表示。此曲线的使用和曲线在AISCM将在后面的部分讨论。
212 6章
在 的 以上 方程 的 术语 0。7Fy Sx 是 也 述 自 作为 Mr, 的 对应 自 的限制 屈曲 时刻 当 Lb = Lr 和 是 的 过渡 点 之间 弹 塑性 和 elas-tic lateral–torsional 屈曲 (参见位置Mr 在图 6-5)。
对于紧凑型 I 形形状和 C 形, 当Lb gt;Lr, 公称弯曲强度为
Mn =F铬 Sx 这Mp,
(6-11)
=Cbp2和A1 0078 Jc 的Lb b2,
F
(6-12)
地方
a b
Ct
Lb 2
rTs
Sxho
rTs
Cb =力矩梯度因子
12。5M麦克斯
C
=2。5M
麦克斯
3MA
4MB
3MRm 这3.0,
(6-13)
M麦克斯 =无支撑段中最大矩的绝对值,
MA =绝对值的时刻在1frasl;4无支撑段的点,MB =无支撑段中线的矩绝对值,MC =绝对值的时刻在3frasl;4 无支撑段的点,Rm =截面对称性 因素
=1.0 为双重对称成员 (I 形状)
=1.0 为单独单曲率弯曲中的对称截面
a b
=0。5 2IYc 2
Iy
对于受反向曲率的单个对称形状
弯曲 和 (6-14)
IYc =压缩法兰的惯性力矩关于y轴.
为 双 对称 形状 IYc 是 大约 平等 自 Iy/2。 为 反曲率弯曲,IYc 是小的惯性力矩 法兰。
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[468169],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


