英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
基于SYSWELD的板式样堆焊有限元分析
S.K. Bate*, R. Charles, A. Warren
摘要
焊接的温度场与应力场分析已实现了软件模拟,SYSWELD可以模拟板试样的单元,热源由可编程的Goldak双椭球热源模型表示。该模型的参数由焊接参数、宏观数据和热电偶数据而定义,应力分析是基于定义于软件的数据库中拉伸数据下的各向异性的模型,在1400摄氏度的温度下进行退火。本文介绍的热量源拟合,随后是温度与应力分析,并介绍了结果。
1.引言
有限元法和实验法分析焊接残余应力是相当普遍的,但这些方法的局限性还不完全清楚,它们需要得到证实。然而,当两者方法相互映证时,结果证明了两种方法足够的可行性,得到的的残余应力分布可以放心地用于评估。将焊接过程进行数据化模拟的方法很早就有了,计算机的计算能力的增强已使模型单元的细化程度和复杂性大为增加,这些方面意味着在某些情况下的简化和假设都必须与残余应力近似。因此在这些方法的准确性上存在着不确定性,往往近似程度不够,即残余应力上限在许多情况下,仍需要依赖于含有完整结构的组件性能来评估。
英国的一项工作计划[ 1 ]目前正在进行中,以发展一种用于残余应力预测的方法,在各种简化和假设的条件下预测应力的大小,并确定的局限性的各种建模技术。这将包括热源在极高温度下的模拟,对材料进行退火处理,循环硬化或软化,蠕变以及相变换。焊接过程的虚拟与仿真一直是近年来焊接领域的研究热点。对于焊接过程而言,其物理现象本身非常复杂,是一个涉及高温电弧物理、传热、冶金和力学的复杂过程,因此在建立精确的物理模型方面存在着较大的难度。由于焊接过程温度梯度很大,在空间域内大的温度梯度导致严重的材料非线性,产生求解过程中的收敛困难和解的不稳定性;在时间域内大的温度梯度决定了瞬态分析时离散程度上的加大,直接导致求解时间步的增加。由于上述原因,焊接过程数值模拟的研究长期以来一直停留在二维水平上。近年来,随着计算机技术的发展,焊接过程三维数值模拟成为该领域的重要研究课题。由于焊接过程的复杂性,焊接过程的三维数值模拟仍停留在基础性研究阶段,且大多是以典型接头作为研究对象,远未达到应用于实际结构的水平。使用测试也将由基准而来,这主要是将循环测试、分析预测与各种测量技术相结合。最初的工作考虑了板状试样的奥氏体单焊缝,见下面图1,这是一个欧洲正在研究的基准网络中的一个网格模型[ 2 ]。一组被定义为软件的数据库[ 2 ]的残余应力数据,包含了焊接残余应力的测量结果及以有限元法模拟的板件上的一个单元的数据。本文介绍了一种利用有限元的方法来分析试样元素的分析元软件SYSWELD [ 3 ]。试样的几何形状被建模的3D。热源由Goldak定义模型[ 4 ]和模型参数的拟合。一个各向同性的刚性模型用来模拟材料状态,从而来分析材料焊接的一些结果。
2.有限元模型
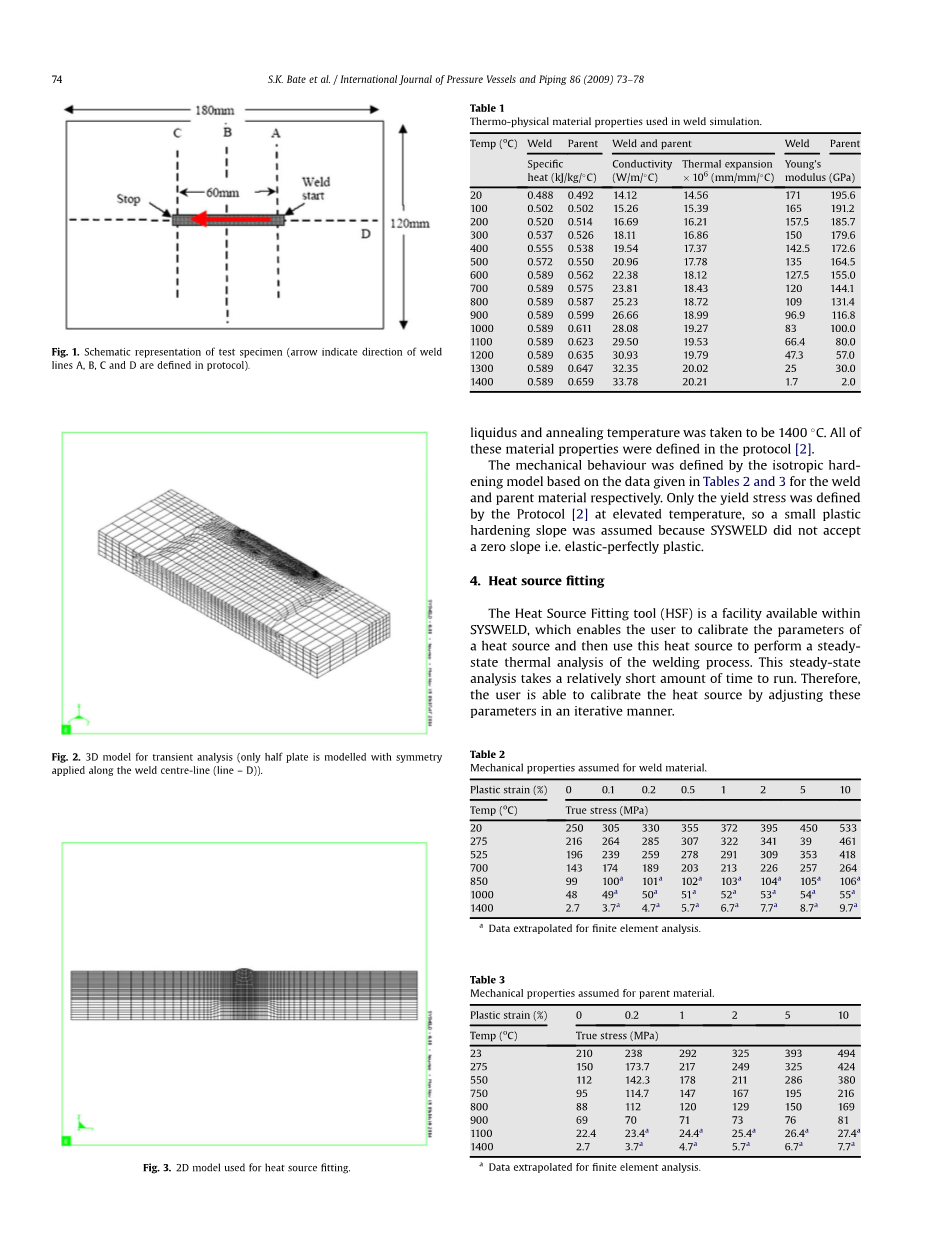
图1所示为板状试样的示意图。该板件的三维模型已生成。存在一条对称线(焊缝中心线)如图1所示,因此只用模拟该样本的一半,如图2所示。该模型包含20320个八节点实体单元。焊接细节配置文件被定义软件的数据库中[ 2 ]。二维模型也按照SYSWELD热源配件要求设定,见后面的部分,具体见图3,该模型包含2312线性元件。
3.材料的性能
与温度相关的热传导率,具体热容量,热膨胀系数和杨氏模量可以在表1中找到。密度为7966 kg/m3,泊松比为0.294,均与温度无关。在这一分析,未考虑融合的潜热,这个泊松比为0.294与两个独立的温度无关。而且在这一分析中,未考虑融合的潜热,所以这个液相线温度和退火温度为1400 C,所有这些材料的特性被定义在软件的数据库中[ 2 ]。被定义的应力状态的各向同性硬化基于表2和3的焊接数据的模型和母材。只有屈服应力被定义 [ 2 ]在高温下,所以一个小塑料硬化坡假定因为SYSWELD不接受一零坡即弹塑性。
图1.试验样品的示意图(箭头指示的焊接线,乙,丙和丁的定义在数据库中)。
图2.三维瞬态分析的模型(只有一半板,是沿焊缝中心线的对称应用)
图3.用于温度测量的二维模型。
图4.Goldak双椭球热源模型的图形表示--热源在向正方向移动。
4.热源拟合
热源拟合工具(HSF)是一个SYSWELD的一个功能模块,这使用户校准参数热源,然后用这个热源进行稳态焊接过程的热分析。这种稳态分析需要一个相对短的时间来运行。因此,用户可以通过调整这些热源来校准热源迭代方式的参数。用户可以通过调整这些热量来校准热源在一个迭代的方式为用户校准的热源是可能的参数双方法的结合。通常解析方法较简单,意义明确,易算,但由于它的假设太多,难以提供在熔合线、热影响区处的精确计算结果,而且考虑不到电弧力对熔池的冲击作用。采用有限元或有限差分法,应用高斯分布的表面热流分布函数计算,可以引入材料性能的非线形,可进一步提高高温区的准确性,但仍未考虑电弧挺度对熔池的影响。从球状、椭球、双椭球热源分布,每一种方案都比前一种方法更准确,但也伴随着计算量的增加,使这些热源分布函数更利于应用有限元法或差分法在高速计算机上进行计算。而且实践也证明能得出较满意的模拟结果。对于通常的焊接方法如手工电弧焊、钨极氩弧焊,采用高斯分布的函数就可以得到较满意的结果。首先,温度等高线图显示预测的焊接熔合区可以与一个宏观的焊接。其次,热电偶读数在焊接过程中能获得与温度由之产生的数据。HSF支持许多不同的预定义的热源模型,所有代表特定的焊接工艺。因为这分析关注与TIG焊,双椭球模型选择。双椭球模型的基础上的工作Goldak [ 4 ]。该模型使用下面的方程来定义热通量(问)内的前部和后部区域的热量源,在这些区域通过下标1和2表示分别:
a、b和c描述的热量来源的尺寸,问是电源从焊接电源输入,五是焊接速度,吨是时间,是一个滞后因素定义在Tfrac14;0热源的位置和定义的馏分的热沉积在任一区域,在thorn;frac14;F1 F2 2。图4显示了双椭球热源。
5.校准
使用二维热源拟合分析图3所示的模型。板的初始温度设定到20摄氏度的一组温度依赖性的传热系数被应用到模型的外表面。这些系数被计算为代表的影响对流和辐射,如表4所示。功率输入被计算为效率的乘积,热输入和焊接速度。定义在软件的数据库中的焊接热输入速度和效率为80%假定,高斯参数描述的热源然后反复调整直到HSF生产熔融(融合)区一样,在一个宏观的测试片,看图5。熔合区是在或以上的材料图1400显示了最后的熔合区,由之预测,焊接热影响区(HAZ)在750和1400之间的轮廓显示为一系列的轮廓没有可识别的微观结构特征,他们可以相比较[ 5 ]。最大预测温度范围内融合区为2193角,表5为最终热源从所得到的参数。焊接过程中存在很大的非线性. 它既有大应变问题即几何非线性问题, 又有材料非线性如塑性变形、粘塑性、蠕变等. 如果分析选项设置不当, 通常会导致计算难收敛。
图5.焊缝横截面形貌。
图6.使用热源拟合工具模拟的结果(焊缝熔合区温度在1400℃以上的地区)。
图7.热电偶的位置(点0,0,0表示测量基准点)。
在载荷模型的选取与施加焊接热过程的研究中, 人们提出了一系列的热源计算模式. 对于通常的焊接方法(如手工电弧焊、钨极氩弧焊) , 采用呈高斯函数分布的热源模型可以得到较满意的模拟结果. 但对于电弧冲力效应较大的焊接方法, 如熔化极氩弧焊和激光焊, 常采用双椭球形热源分布函数. 为求准确, 还可将热源分成两部分, 采用高斯分布的热源函数作为表面热源, 焊件熔化部分采用双椭球形分布函数作为内热源.在sysweld中, 对于焊接热源载荷可采用热流密度或生热率两种形式施加. 对于表面堆焊问题, 忽略熔覆金属的填充作用时, 将热源以热流密度的形式施加, 可以得到较满意的计算结果. 但对于开坡口的焊缝或填角焊缝等, 应将热源作为焊缝单元内部生热处理, 以生热率的形式施加, 同时考虑金属的填充作用, 采用生死单元的方法, 逐步将填充焊缝转化为生单元参与计算中.施加移动的焊接热源时, 可利用移动电弧中心坐标的方式来实现.焊接应力场的计算中, 其载荷是温度场的计算结果, 施加载荷时, 读入热分析的节点温度并指定相应的时间点或载荷步即可. 但是, 焊接过程中, 熔池区的金属处于熔化状态, 即进入零力学性能状态, 其所有的应力应变将消失, 而当熔池由液体转变为固体时, 进入无应变历史的初始状态. 对此, 可采用生死单元的方法, 在每一步热应力计算时, 将对应的温度场的计算结果进行选择, 超过熔点的单元令其死掉, 而低于熔点的单元将其激活。
图8.热电偶的读数与温度数据通过SYSWELD热源拟合工具预测比较。
6.瞬态分析
在HSF工具瞬态分析定义的参数的基础上,运行一段时间,包括板冷却到环境温度后焊的焊缝运行和足够的时间,分析需要118次的增量,并采取了约2.5小时完成,整个温度历史被保存为随后的机械分析,使用各向同性硬化模型和小位移理论进行机械分析,退火是假定发生在1400 C°,退火用在这里是指材料的熔体和有限元代码,ABAQUS的温度,假定材料失去其强化记忆,即现有的加工硬化的效果是通过设置塑性应变为零删除。随着热源不断向截面接近,焊缝中心区的压应力也不断增大,达到最大值后,压应力逐渐减小,直到热源中心与该截面重合时,应力为零。当热源离开该截面,焊缝中心区域的拉应力逐渐增大,同时热影响区附近的压应力也逐渐增加。该截面随着热源远离而逐渐冷却,拉应力逐渐达到最大值,接近母材的屈服极限。而焊缝两侧压应力最大值逐渐减小,压应力的横向范围加大,直到冷却到较低的温度后,焊缝两侧基本全为压应力。在焊接过程中,焊接区以远高于周围区域的速度被急剧加热,并局部熔化。焊接区材料受热膨胀,热膨胀受到周围较冷区域的约束,并造成(弹性)热应力,受热区域温度升高后屈服极限下降,热应力可部分超过该屈服极限:结果,焊接区形成了塑性的热压缩:冷却后,比周围区域相对缩短。因此,这个区域就呈现拉伸残余应力,周围区域刚承受压缩残余应力分析需要199次的增量,并采取了27.5小时完成。由于机械暂态分析所产生的输出文件的非常大的性质,它是不实际的记录每一个时间步长。因此,只有最后一个步骤的焊接过程和冷却期间被记录。
图9. 模拟的沿焊缝中心线的三维横向应力,(应力显示为兆帕)。
图10。模拟沿焊缝中心线的纵向应力,(所示的单位MPa)。
图11.在焊缝中的横向应力(在对称面上)(应力单位为兆帕)。
图12.纵向应力在焊缝中的分布(单位为兆帕)。
图13.模拟的在焊缝中心线上的残余应力,2毫米以下的板的上表面(S11–横向,S22–纵向,S33–截面)。
理论上,在焊接过程中,焊缝及近焊缝区在热源到达时急剧升温,并出现局部熔化,其升温速度远远高于远焊缝区及板边缘,焊缝及近焊缝区受热膨胀,在远焊缝区及板边缘较冷区域的约束下形成弹性热应力。焊缝及近焊缝区材质的屈服极限是会受到高温影响而降低,而热应力也会因此材料的屈服使得一些部分会达到一定的极限,于是焊缝及近焊缝区形成了塑性的热压缩。热源离开后,焊缝及近焊缝区由于冷却而比远焊缝区及板边缘相对变窄和缩短,造成焊缝及近焊缝区呈现拉应力,远焊缝区及板边缘呈现压应力
7.结果
图6所示的预测的熔合区被认为是与分析提供了合理的软件的数据库。那里然而,在温度预测的一些差异用热电偶测量,见图8。这个最可靠的热电偶读数被认为是那些在T5,T7,T9,对应于近稳态条件与平均值的预测峰值温度的比较热电偶测量[ 2 ]显示在表6。最好的软件的数据库是实现与远场热电偶T5和底部表面的热电偶,T9。差异随着近场(T1,T2,热电偶和T3)可能是由于电弧发光,而后来的切片标本,显示这种融合的边界与那些的软件的数据库提供的测试珠。1在该软件的数据库中也有一个延迟。不在焊接开始时的火炬运动通过这种分析模型,从而有助于在在T1和T4的预测。热电偶的响应(T5,T7,T9)进行校准焊接效率[ 5 ],从中估计75%得到的,这是略低于所使用的假设值分析。这意味着更多的热量被输入到模型中预测的温度高于那些测量,看到表6。
预测横向(垂直于焊缝)和纵(平行于焊缝)残余应力的试样在图1中显示的是纵向平面(图)。图中焊缝中心。9和10。相应的应力跨越板(线)的宽度在图中显示。十一和12。沿焊缝的长度的应力绘制图13。它显示了不同的峰附近的开始和停止位置焊接运行。与测量值相比,预测的应力[ 6 ]沿着这些线。残余应力的趋势是合理的然而,预测的应力幅度超过预测的模型。这可能是由于使用各向同性硬化一般过度预测的残余应力,特别是在纵向方向。为了了解一些差异,这是在这一分析中出现的测量数据,进一步的敏感性分析[ 7 ]使用双线性运动硬化模型显示更好的软件的数据库与测量应力,而比较结果[ 6 ]表明,使用一个非线性运动硬化模型给出更好的软件的数据库。敏感性分析表明,降低了效率因此,热输入将减少残留强调,但这种效果是不一样的选择硬化模型。
8.结论
预测的熔合区应力数据与软件的数据库相似程度很高,热电偶(T5)测量的温度数据也与之相合,在基板试样测定的温度场(T9)的不同是由于使用假定的焊接效率为80%而不是一个推断的值75%,这个各向同性的模型的使用导致应力过
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[148238],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。