嵌入式相空间中电子鼻传感器漂移的混沌时间序列预测外文翻译资料

 2022-06-28 11:06

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

嵌入式相空间中电子鼻传感器漂移的混沌时间序列预测

张磊，田凤春，刘首琼，邓利军，彭雄伟，尹信

（重庆大学通信工程学院，重庆市沙坪坝区沙生街174号，400044；

计量与质量检验所，重庆，401123）

摘要：传感器漂移在长期观测中表现为混沌行为和不可预测性，使构造合适的传感器漂移处理变得困难。这篇论文的主要目的是研究了一种在相空间中基于混沌时间序列的新的传感器观测模型。该方法实现了基于相空间重构(PSR)和径向基函数(RBF)神经网络的传感器基线和漂移的长期预测。PSR可以存储混沌吸引子的所有性质，并清晰地显示出时间序列的运动轨迹，因此PSR利用RBF神经网络实现了长期漂移预测。通过对Lyapunov指数的分析和一年中三种金属氧化物半导体传感器的实验观测数据表明，该传感器具有明显的混沌特性。结果表明，该模型能够对传感器基线和漂移时间序列进行长期、准确的预测。

关键词：传感器漂移；混沌时间序列；长期预测；相空间重构；径向基函数神经网络

Chaotic time series prediction of E-nose sensor drift in embedded phase space

Lei Zhang, Fengchun Tiana, Shouqiong Liub, Lijun Dang, Xiongwei Penga, Xin Yin

(a College of Communication Engineering, Chongqing University, 174 ShaZheng Street, ShaPingBa District, Chongqing 400044, China b Academy of Metrology and Quality Inspection, Chongqing 401123, China)

Abstract:Chemical sensor drift shows a chaotic behavior and unpredictability in long-term observation which makes it difficult to construct an appropriate sensor drift treatment. The main purpose of this paper is to study a new methodology for chaotic time series modeling of chemical sensor observations in embedded phase space. This method realizes a long-term prediction of sensor baseline and drift based on phase space reconstruction (PSR) and radial basis function (RBF) neural network. PSR can memory all of the properties of a chaotic attractor and clearly show the motion trace of a time series, thus PSR makes the long-term drift prediction using RBF neural network possible. Experimental observation data of three metal oxide semiconductor sensors in a year demonstrate the obvious chaotic behavior through the Lyapunov exponents. Results demonstrate that the proposed model can make long-term and accurate prediction of chemical sensor baseline and drift time series.

Keywords:Sensor drift;Chaotic time series ;Long-term prediction;Phase space reconstruction;Radial basis function neural network.

  1. 介绍

人工嗅觉系统，如电子鼻(E-nose)，正成为监测环境领域空气污染的一种很有前途的方法。化学传感器已被广泛应用于挥发性有机化合物的分析。E-nose是一种仪器，它使用传感器阵列的化学传感器，但只有半选择性气体传感器与模式识别，并提供更高程度的选择性和可逆性，因此有广泛的应用范围[1.2]。然而,传感器通常在实际应用中运行一段时间后，老化会减少传感器的寿命。传感器漂移由传感器系统中未知的动态过程引起，包括中毒、传感器老化或环境变化[3]漂移将会降低传感器的选择性和灵敏度，而由漂移传感器组成的电子鼻将失去其作为一个可用的监视器的有效性，因为之前的模式识别模型无法适应漂移的阵列空间。因此，传感器响应的渐变和不可预测变化被认为是电子鼻发展中最具挑战性的问题[4]。

近年来，研究人员对许多漂移的反作用力方法进行了研究。最常用的方法是多元组件修正[5]、主成分分析[6.7],自适应基于进化算法漂移校正[8.9],正交信号修正,和基于估计理论的漂移补偿[10]。然而，所有的方法都假设长期的传感器漂移趋势可以通过主成分空间的漂移方向或样本的分布来跟踪。不幸的是，长期的传感器漂移没有规律的趋势，从长远来看传感器漂移并不总是正或负的。此外，以前的方法只能在计算机上离线分析，在实际应用中很难应用。因此，通过一年内对传感器响应的长期观测，我们研究了长期传感器响应的混沌特性，提出了一种基于相空间重构和RBF神经网络的混沌时间序列预测方法，并提出了一种新的漂移预测模型。

混沌是非线性动力系统的普遍现象。混沌是一种不规则的运动，在确定性条件下，由确定性非线性系统表现出的看似不可预测的随机行为。混沌时间序列预测是基于相空间重构(PSR)的，其目标是根据目前的观测序列，找到吸引子的嵌入方式、尺寸和时间延迟[11.12]。时间序列将在不改变其拓扑结构的情况下重构系统的吸引子，适当的时延将把预测问题转化为在相空间的一个短期的进化过程。相空间重构保留了吸引子的性质。因此，对于一个未知漂移模型，在嵌入式相空间漂移预测的应用混沌吸引子理论是合理的。

  1. 数据

2.1 长期传感器基线数据

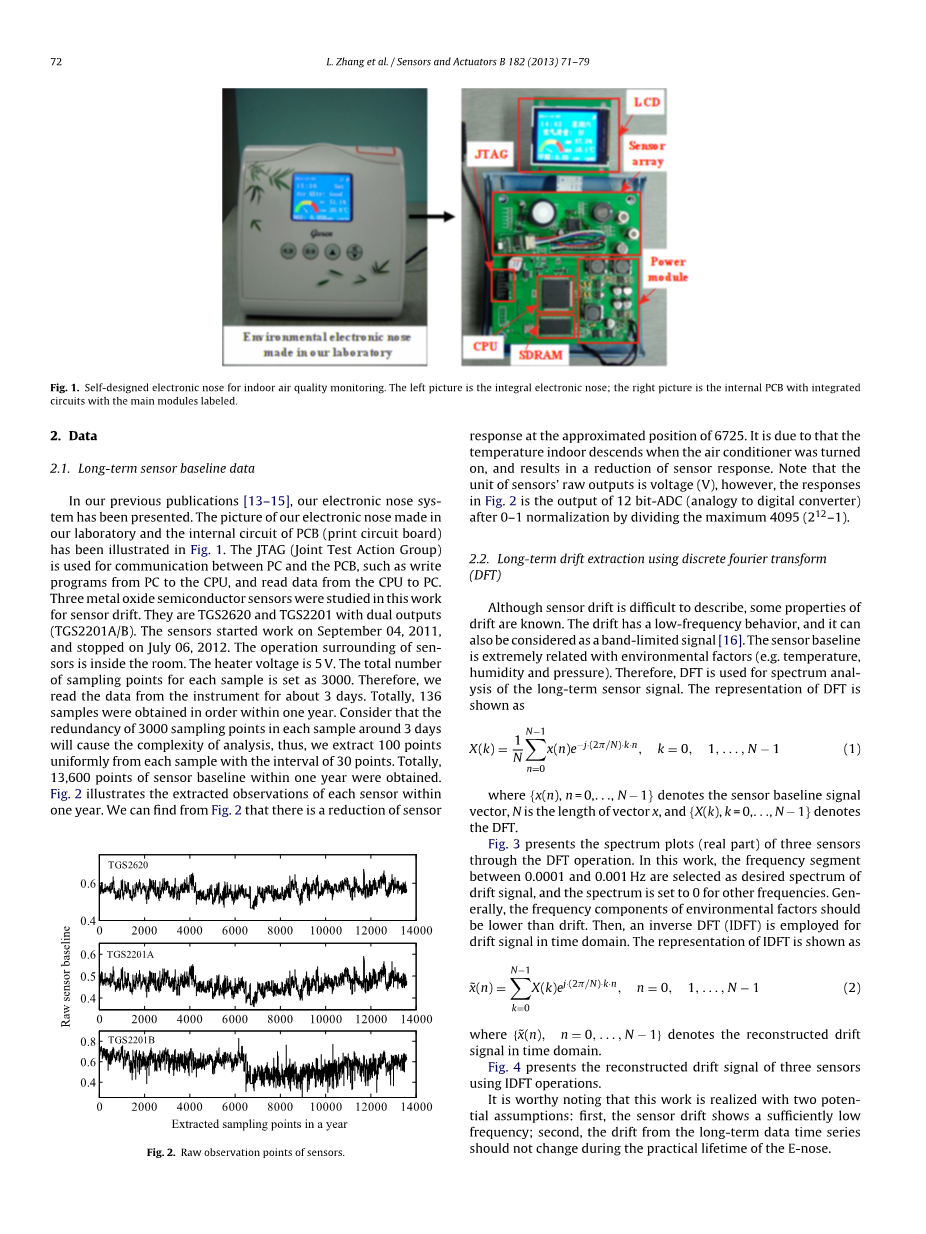
在我们之前的出版物里[13-15]，我们的电子鼻系统已经被展示出来了。我们实验室的电子鼻图像和PCB(印刷电路板)的内部电路如图1所示。JTAG(联合测试操作组)用于PC和PCB之间的通信，例如从PC到CPU的编写程序，以及从CPU到PC的读取数据。研究了三种金属氧化物半导体传感器在传感器漂移中的应用。他们是TGS2620和TGS2201的双输出(TGS2201A/B)。传感器在2011年9月4日开始工作，并于2012年7月6日停止。传感器周围的操作在室内。加热器电压为5V。每个样本的采样点总数为3000。因此，我们从仪器上看了大约3天的数据。共计136个样品在一年内获得。考虑在3天左右的每个样本中，3000个采样点的冗余将导致分析的复杂性，因此，我们从每个样本中抽取100个点，间隔为30个点。在一年之内，获得了13600点的传感器基线。图2说明了在一年内提取的每个传感器的观测结果。从图2可以看出，传感器的减少在接近位置6725时的响应。这是由于空调打开时室内温度下降，导致传感器响应减少。注意，传感器的原始输出的单位是电压(V)，然而，图2中的响应是12个位- adc(与数字转换器的类比)，在0-1归一化之后，将最大4095(212-1)划分。

图1 自行设计的电子鼻用于室内空气质量监测。左边的图像是整体电子鼻;右边的图片是内部电路板，集成电路与主模块标记

图2 传感器的原始观察点。

2.2 利用离散傅里叶变换进行长期漂移提取

虽然传感器漂移难以描述，但有一些漂移特性是已知的。漂移有一个低频的行为，它也可以被认为是一个带限信号[16]。传感器基线与环境因素(如温度、湿度和压力)极为相关。因此，DFT用于长期传感器信号的频谱分析。DFT的表示形式如下所示。

在{ x(n),n = 0,。,nminus;1 }表示传感器信号基线向量,n是向量x的长度,{ x(k),k = 0,。,nminus;1 }表示DFT。

图3通过DFT操作给出了三个传感器的谱图(实部)。在该工作中，选择0.0001和0.001 Hz的频率段作为漂移信号的期望频谱，其他频率的频谱被设为0。一般来说，环境因子的频率分量应该小于漂移。然后，采用逆DFT (IDFT)对时域的漂移信号进行求解。IDFT的表示形式如下所示。

其中，{x (n)， n = 0，. .， n 1}为时域重建的漂移信号。图4给出了利用IDFT操作的三个传感器的重构漂移信号。值得注意的是，这一工作是通过两个可能的假设来实现的:首先，传感器漂移显示了足够低的频率;其次，长期数据时间序列的漂移在实际的E-nose生命周期中不应发生变化。

图3 三传感器的DFT谱图

图4 利用IDFT重构传感器漂移信号

3 混沌时间序列预测

3.1 相空间重构

相空间重构(PSR)是对混沌动力学系统进行分析的基础理论[17]。利用该定理证明了在拓扑结构中具有与动态系统相同的相位空间的一维混沌时间序列可以重构相空间。在重构相空间中采用了判别、分析和预测，因此PSR是混沌时间序列研究的关键。嵌入维数m和时间延迟是PSR中最重要的变量[18-23]。研究人员对m的选择进行了很好的研究。本文采用假近邻法[18]来确定嵌入维数m，利用自相关函数计算时滞[18-19]

给定混沌时间序列{x(n)， n = 1，. .， n}，重构相空间可以表示为

其中t(1)、(m 1) 1、m (m2,3，. .)是嵌入维数，提供m 大于等于2D 1, D为吸引子的分形维数。

为了清楚起见，我们将公式(3)展开如下。

符号T表示向量的转置。Lyapunov指数是一种定量描述混沌吸引子的有用工具，它有效地测量混沌轨道对初始条件的敏感性，并对复杂系统的吸引子动力学进行量化。当时间序列的李亚普诺夫指数为正时，时间序列将变得混沌[17]。利用经典的Wolf-method[24]来计算李雅普诺夫指数的计算。例如，在PSR分析中，我们通过对Lorenz系统的数值积分来生成一个时间序列[25]。洛伦茨系统的表示形式如下所示。

其中x与对流运动的强度成正比;y是水平温度变化的比例;z是垂直温度变化的比例;r和b是常数。对于分析，参数r和b分别设置为25、3和50;集成的步骤大小设置为0.01;y的初始值是[- 1,0,1]T。图5说明了洛伦茨吸引子的PSR，其中嵌入维数m = 3，时滞= 1。

3.2 预测模型

在混沌时间序列预测中，利用RBF(径向基函数)神经网络[26]对每个传感器嵌入相空间的吸引子进行跟踪。在中提到了利用RBF来模拟表示时间序列数据的奇异吸引子。RBF神经网络[27]是由三层组成的正向反馈人工神经网络。输入节点的数量取决于嵌入维数m。输入信号是重建的X(t)(t = 1。Nminus;minus;1)(米)在相空间。在隐层中，使用高斯函数作为激活函数。PSR中RBF神经网络预测的结构如图6所示。

结合Eq.(4)，可以显示训练输入矩阵。

用式(4)和(6)求出P的展开式。

然后将训练目标的向量表示为。

本文分别构建了TGS2620、TGS2201A和TGS2201B三个模型。混沌时间序列预测可以分为两步:相空间重构和RBF神经网络学习。我们将该方法应用于洛伦茨吸引子预测的实例分析。我们在Lorenz序列中选择5000个点进行预测，其中前1000点用于RBF神经网络学习，剩下的4000点作为测试。试验结果如图7(a)和(b)所示，分别说明了洛伦兹混沌时间序列的预测和预测残差。在图7中我们可以看到Lorenz混沌时间序列的预测成功地使用了所提出的模型。已知的统计数字RMSEP(根均方误差预测) [28]也用于定量测量该工作中的传感器基线和漂移预测模型。它可以表示为

其中N为检验序列s的长度为真序列，s为预测输出。在理想情况下，如果预测没有错误，那么RMSEP = 0。4 结果

4.1长期传感器数据的混沌特性

长期传感器响应的混沌特性已得到证实。通过对{x(n)， n = 1，. .， n}各传感器的分析，TGS2620、TGS2201A和TGS2201B的自相关函数法计算的时间延迟分别为22、24和23。嵌入维数计算为m = 3。图8中的三个子图说明了三维(x(t)、x(t )、x(t 2))的PSR图，每个传感器在一年的时间内提取了13600点，显示了PSR中传感器的运动轨迹。通过图8的PSR图，我们可以发现每个传感器的运动轨迹具有混沌吸引子的相似特征。

此外，为了进一步确认，使用Wo

全文共12293字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[10557]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章