
英语原文共 6 页,剩余内容已隐藏,支付完成后下载完整资料
石墨烯纳米结构中中红外等离激元的阻尼途径
等离激元是电子集体振荡的量子。等离激元如何失去能量(或阻尼)在等离激元科学与技术中起着至关重要的作用。石墨烯等离激元由于潜在的低阻尼率从而特别令人感兴趣。然而,迄今为止,阻尼通路并没有明确的实验阐明。在这里,我们展示了小至50nm(模型面积大约为1*10-3mu;m2)的石墨烯纳米结构中的中红外(4-15mu;m)等离激元。我们还通过石墨烯固有的光学声子和边缘散射揭示了阻尼通道。当石墨烯光学声子通过散射而造成阻尼时,等离激元的寿命可达到20fs甚至更低。此外,相比于非极化的DLC基底,石墨烯纳米结构下的SiO2基底的表面极化声子导致等离激元散射和阻尼发生显著变化。我们的研究为石墨烯在亚太赫兹到中红外波段的等离激元波导、调制器和探测器中的应用做准备。
等离激元纳米结构能够使局域电磁能量超过衍射极限,在超材料、量子光学、太阳能光电、光电探测器和生物传感方面都有广泛应用。石墨烯等离激元由于独特的可调谐性、可预测的长等离激元寿命以及高度电磁局域化,引起了极大的兴趣。最近研究发现图案化石墨烯微结构在太赫兹频率范围内的电磁响应主要受等离激元激发狄拉克费米子的控制。这里,我们通过将石墨烯剥离成50nm大小的纳米结构,展示了二维等离激元的自然散射引起的石墨烯等离激元在中红外区的机械共振。与等离激元共振频率在太赫兹波段的石墨烯微观结构相比,中红外区等离激元响应受基底声子和石墨烯固有的光学声子之间的相互作用的影响更加强烈。这些相互作用导致等离激元散射的重整,调控着等离激元的寿命以及传播距离。此外,还明确发现了边缘效应对中红外等离激元响应的影响,不仅补充了之前在类石墨烯纳米结构上的研究 ,也是对金属纳米结构中局域等离激元研究领域的补充。
实验和方法
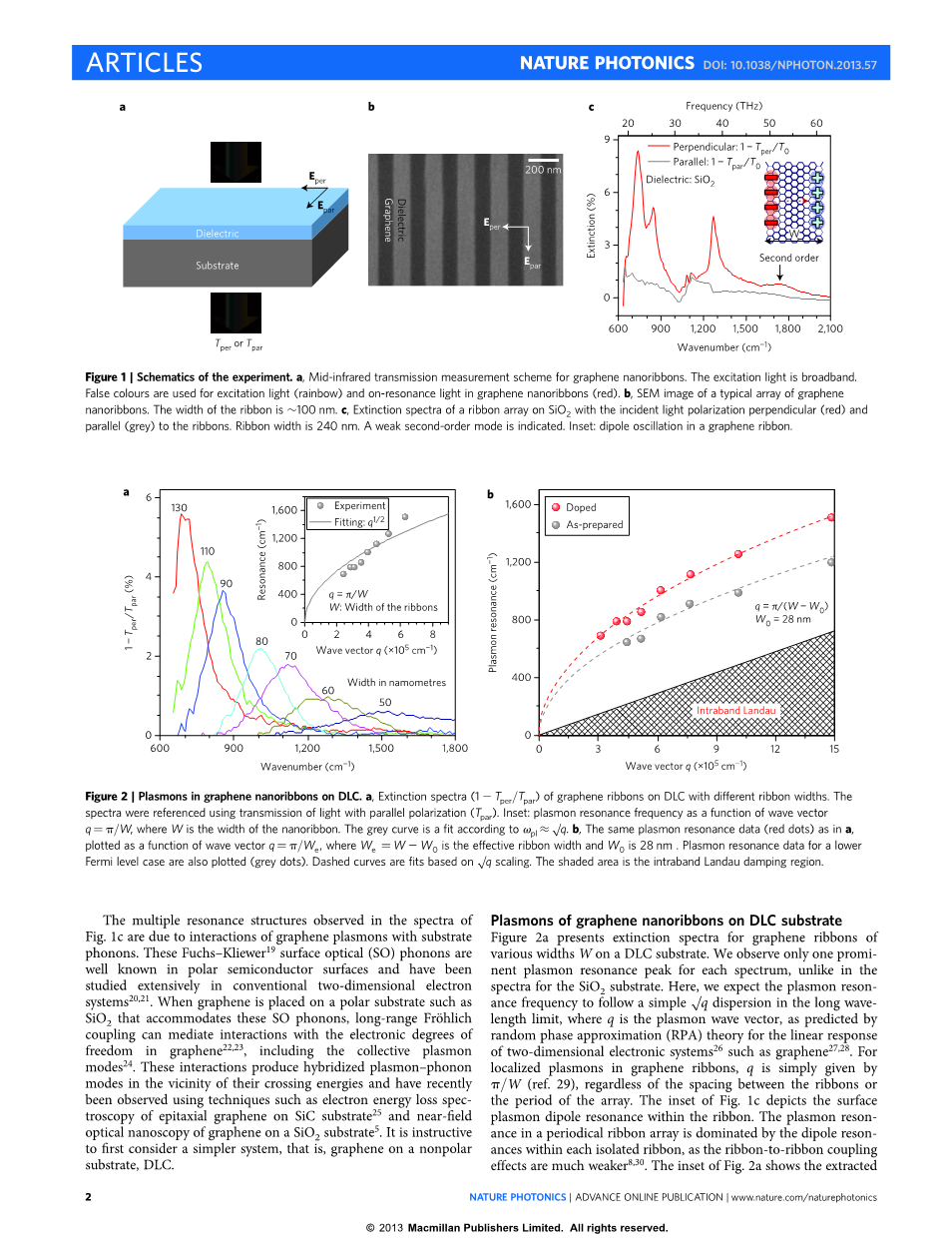
石墨烯纳米结构如纳米条带阵列、反点和纳米圆盘阵列都是在化学气相沉积法(CVD)生长的石墨烯上通过电子束刻蚀得到的。不同的衬底如SiO2和DLC被用于高电阻的硅片之上。用于这些结构的中红外透射测量装置(如图1a)是具备傅立叶变换红外光谱仪(FTIR)的红外显微镜,与宽带偏振器配合使用。制备和测试过程的细节在方法里面给出。
石墨烯纳米条带和纳米圆盘中等离激元响应的定性行为类似,除了石墨烯纳米条带存在明显的偏振依懒性。在这里,我们关注石墨烯纳米条带(图1b展示了其典型的SEM图像)。这些石墨烯纳米条带阵列的电磁响应用消光光谱
1-Tper/T0和1-Tpar/T0表示,其中Tper和Tpar是电场方向垂直和平行于条带的
通过条带阵列的透射光。T0是通过没有石墨烯的基底的透射光。图1c展示了SiO2基底上宽度约为240nm的条带阵列的消光光谱。两条曲线分别表示入射光偏振垂直(红色)和平行(灰色)于条带的结果。内部插图描绘了石墨烯纳米条带的偶极振荡。
由于局域等离激元的激发,垂直极化的消光光谱出现了明显的共振峰。这里的多个共振峰与通常表现为单一的强共振的石墨烯微观结构的远红外光谱形成鲜明对照。由于没有等离激元激发,平行偏振光谱除了在1000cm-1和1200cm-1之间有小的特征峰之外没有共振峰。这些特征峰和SiO2基底急剧变化的动态介电函数相关,并且比较弱(消光强度lt;1%)相比于那些明显的等离激元峰。在中红外波长区域,如果偏振光平行于高度掺杂的石墨烯条带(如本文所述),由于泡利不相容原理阻挡带间跃迁以及高频率时较弱的自由载流子带内跃迁,它与光的相互作用非常微弱。因此,平行条带的偏振光透射光谱(Tpar)和参考值(T0)特别接近。在后面的介绍中,它将作为垂直偏振光消光光谱的参考值。也就是在本文的其他地方,将消光光谱定义为1-Tper/Tpar(参见方法)。
图1c光谱中观测到的多重共振结构是石墨烯等离激元和基底声子相互作用的结果。这些Fuchs-Kliewer表面光学声子(SO)在极化半导体表面很常见,并且在传统的二维电子系统里已经被广泛研究。当石墨烯被放在像SiO2这样具有表面光学声子的极性基底上时,长程Frouml;hlich耦合能够调节石墨烯中电子自由度的相互作用,包括集体等离激元模式。这些相互作用在它们的杂化能量附近引起了杂化等离激元-声子模式,并且最近已经通过一些技术例如SiC基底上外延生长石墨烯的电子能量损失谱和SiO2基底上石墨烯的近场光学纳米技术观测到。首先考虑一个更简单的系统,即非极性基底DLC上的石墨烯,这很有益。
图1 . 实验示意图. a,石墨烯纳米条带的中红外透射测量方案。激发光是宽带的。假色用于石墨烯纳米条带(红色)中的激发光(彩虹)和共振光。b,典型的石墨烯纳米条带阵列的SEM图像。条带宽度为100nm。c,入射光偏振垂直(红色)和平行(灰色)于SiO2条带阵列的消光光谱。条带宽度为240nm。 结果显示了弱二阶模式。插图:石墨烯带中的偶极振荡。
DLC基底上石墨烯纳米条带等离激元
图2a展示了DLC基底上不同宽度W的石墨烯条带的消光光谱。我们发现与SiO2基底的光谱不同,每个光谱上只有一个显著的等离激元共振峰。这里,我们期望等离激元共振频率在长波极限处符合一个简单的radic;q色散关系,其中q是等离激元波矢,正如通过随机相位近似(RPA)理论预测像石墨烯这样的二维电子系统的线性响应。对于石墨烯条带局域等离激元,q=pi;/W,忽略条带间距或周期性阵列。图1c的插图描述了表面等离激元在条带内的耦极共振。周期性条带阵列中的等离激元共振受每个独立条带的耦极共振的控制,因为条带和条带间的耦合效应非常微弱。图2a的插图展示了图2a中得到的等离激元频率与pi;/W的关系,显然与理论预测的wpllt;radic;(pi;/W)有明显的不一致。这个差异并不是由于长波近似的衰弱造成的,并且,对于大于10nm的尺寸,量子局域效应所引起的矫正也可以忽略不计。
先前的石墨烯纳米条带实验已经表明,为了解释电子传输行为,通常需要假定电气宽度小于物理宽度。事实上,通过电子束光刻和氧气等离子体刻蚀技术来制备石墨烯条带会引入原子级缺陷和复杂的边缘化学效应,从而导致边缘的电学行为“不活跃”。因此,我们引入一个有效条带宽度We=W-W0。图2b显示了等离激元频率与波矢q=pi;/We的关系。虚线是radic;q拟合,和实验中两个不同的掺杂水平和W0=28nm很符合。在相同W0的这种方法,我们还可以解释SiO2基底上石墨烯中更多复杂的杂化等离激元-声子散射,我们将在下一章节中讨论。
图2. DLC基底上的石墨烯纳米条带中的等离激元。 a,DLC基底上不同条带宽度的石墨烯条带的消光光谱(1-Tper / Tpar)。使用具有平行偏振(Tpar)的光的透射作为参考光谱。插图:等离激元共振频率和波矢的关系,q=pi;/W,其中W是纳米条带的宽度。灰色曲线是根据omega;plasymp;radic;q的拟合。b,与a中相同的等离激元共振数据(红点),作为波矢q=pi;/We的函数绘制,其中We=W-W0是有效带宽,W0是28nm。还绘制了较低费米能级情况的等离激元共振数据(灰点)。虚线曲线基于radic;q缩放拟合。阴影区域是带内朗道阻尼区域。
SiO2基底上石墨烯纳米条带等离激元
图3a展示了SiO2基底上W为60-240nm的石墨烯条带的消光光谱,在650-6000cm-1的测量频率范围内显示了三个主要的共振峰和一个弱的高阶共振。这些条带的制备条件与DLC基底上条带的制备条件相似,因此他们的掺杂水平相似(见方法)。我们可以确定光谱中的四个关键趋势。第一是色散关系:随着W的减小,所有的共振峰都蓝移,但是移动速度不同。特别的,峰3向上分散的频率更快。第二是光谱权重,其随着W的减小从峰1向峰2和峰3转移,直到最后,对于Wlt;90nm的光谱,峰3保留了所有的光谱权重。第三个趋势是线宽。峰3的线宽随着W的减小而增大,峰1和峰2的线宽基本保持不变。事实上,上一节讨论的DLC上条带的共振线宽也表现出与图3a的峰3相同的趋势。线宽和等离激元阻尼直接相关,将在下一节讨论。最后一个趋势与线形有关:峰3非常不对称,尤其是对于相对窄的带宽。如补充部分SIII所述,线形可以用Fano谐振模型很好地描述。
光谱中观察到的多个共振是由于等离激元-声子耦合模式,可以用广义RAP理论来描述。直接关系到我们的实验的是损失函数image;[1/εTrpa],定义为逆介电函数的虚部,代表了系统通过等离激元激发耗散能量的能力。我们的计算包括相关的SiO2基底表面光学声子omega;sp1=806cm-1和omega;sp2=1168cm-1和石墨烯固有的光学声子模式omega;op=1580cm-1的相互作用。在补充部分SI中进行了详细讨论。值得一提的是表面极化声子本身能够被光激发,从而导致声子-极化子共振。这已经用红外纳米技术在SiC表面得到证实。与等离激元类似,这种声子-极化子也能显著地局域电磁波。
图3b给出了从图3a的光谱中获得的谐振峰频率上覆盖的损失函数强度图。我们应用与先前章节中使用的相同的方法,也就是说,定义局域等离激元波矢为q=pi;/(W-W0),W0=28nm。使用F2sp1asymp;0.2meV和F2sp2asymp;2meV的Frouml;hlich耦合强度可以与实验观测到的等离激元-声子散射良好的一致性,后者考虑了这种模式的双简并性。Frouml;hlich耦合的值量化了等离激元-声子模式和反交叉能量分裂的杂化,被定义为
(补充部分SI),其中,εhigh和εlow分别是SiO2的高频介电常数和低频介电常数。从杂化等离激元-声子散射的拟合中提取的值虽然其顺序和文献中引用的值相同,但是可以作为更好地估计。此外,具有在这种情况下相同的波矢q=3pi;/(W-W0)的二阶偶极模式也和它的基础模式的散射相符。上述的一致性进一步验证了有效宽度W-W0定义了等离激元动量的前提,并且W0=28nm始终解释了DLC基底和SiO2基底的等离激元和杂化等离激元-声子散射。通过比较没有等离激元-声子杂化(图3b虚线)的等离激元散射和完全RPA计算,我们发现对于qlt;0.4*105cm-1,表面声子效应几乎不会引起简单的radic;q色散关系的偏移。因此,微米条带的等离激元频率遵循Ju和他的同事们之前观察到的简单比例关系。此外,我们注意到损失函数也能描述三个杂化等离激元-声子分支的等离激元峰强度的演化,具有两个反交叉和从低到高频率等离激元分支(峰3)的光谱权重随q的增加转移的特点。(参见补充章节SI)。
图3. 二氧化硅基底上的石墨烯纳米条带中的等离激元。a,SiO2基底上不同带宽的石墨烯条带的消光光谱(1-Tper / Tpar)。为清楚起见,光谱垂直移位。垂直虚线表示石墨烯光学声子频率。b,等离激元频率和峰值1,2和3以及a中的二阶偶极模式峰值对应波矢q=pi;/We的函数关系。计算的损失函数被绘制为二维伪彩色背景。虚线表示不考虑等离子体-声子杂化的等离激元频率。显示出了两个表面极化声子和固有的光学声子频率。有关建模的详细信息,请参见补充部SI。
等离激元阻尼的起源
很多等离激元的应用都得益于较长的等离激元寿命。然而,根据感兴趣的系统,等离激元可以通过辐射过程衰减成光子或者通过带间或带内的朗道阻尼衰减成电子-空穴对。此外,声子的非弹性散射和弹性载流子散射过程也可能有助于等离激元阻尼。前面的两个过程可以排除,因为来自石墨烯纳米结构辐射阻尼的贡献可以忽略不计,如图2b和3b所示,器件中的等离激元激子位于朗道阻尼范围之外。然而,后面两个过程分别对于高等离激元能量(即ћomega;plgt;0.2eV)和小尺寸很重要。最后,与SO声子的相互作用也会影响到杂化等离激元-声子模式的寿命,尤其是当杂化模式的能量接近SO声子时。不同宽度的石墨烯纳米条带使我们能够全面的识别石墨烯等离激元的阻尼机制。
从图2a和3a中的消光光谱,等离激元阻尼率Gamma;P可以使用补充部分SII中描述的简单程序从谐振线宽中提取。图4a绘制了提取的Gamma;P作为有效的带宽We的函数。对于SiO2上的杂化等离激元-声子模式,仅绘制了峰3,因为它存在于所有不同的大小的条带。在DLC基底上,因为等离激元共振能量总是低于光学声子能量,占主导地位拓宽机制涉及弹性载流子散射过程。实际上,它的阻尼率随着We的减小而增加,这表明条带边缘散射。类似的阻尼效果在金属纳米粒子中的等离子体已经被广泛研究。可以使用Gamma;P=Gamma;0 a/We对该效果进行建模,其中Gamma;0是由于本体石墨烯中的载流子散射导致的阻尼率,被测量为~69cm-1,通过相同的DLC基底附近大面积无图案石墨烯
全文共7706字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[2788]
您可能感兴趣的文章
- 复杂热电材料外文翻译资料
- 以自蔓延高温烧结方法制备热电化合物以及燃烧合成的新标准外文翻译资料
- 氮掺杂分级多孔碳作为氧还原反应的高效电化学催化剂的研究外文翻译资料
- 孪晶诱导塑性高嫡合金的设计外文翻译资料
- 含铌先进Fe-Cr-Ni型奥氏体耐热钢富铜相的析出强化在超临界电厂的应用外文翻译资料
- 不同温度下直接能量沉积层状工具钢的弯曲强度外文翻译资料
- BiFeO3的光伏效应外文翻译资料
- 通过氢稳定的MgaPt研究核壳纳米结构Mg@Pt中快速“氢泵”的可视化外文翻译资料
- 一种铱核心环金属有机配体显著地提高了有机太阳能电池 的光伏性能外文翻译资料
- 钠离子电池的高性能阳极材料:三组分共组装法制备层次多孔碳外文翻译资料


