新型温度稳定的（1-x）MgMoO4-xTiO2复相陶瓷的晶体结构、混合行为和微波介电性能外文翻译资料

 2022-08-07 03:08

英语原文共 5 页，剩余内容已隐藏，支付完成后下载完整资料

新型温度稳定的（1-x）MgMoO4-xTiO2复

相陶瓷的晶体结构、混合行为和微波介电性能

摘要：新型温度稳定MgMoO4-xTiO2波介质陶瓷由低温（950°C）下的固相反应过程制备。当Qtimes;f值减小时，相对介电常数增大，并分别提出了相应的改善机理。频率温度系数（tau;f）随正温度系数的TiO2添加量的变化而变化。复合材料的两相混合机制提供理论支撑。当x=0.3时，可获得一个近零值的tau;f（3.2ppm/℃），此时εr=9.13plusmn;0.03，Qtimes;f=11990GHz。0.7MgMoO4-0.3TiO2复合材料被认为是适合作为低温共烧陶瓷微波无线通信应用材料。

关键词：混合物；微观结构；微波介电性能；温度稳定性

1.介绍

随着高频通信产业的迅速发展，微波介质陶瓷在滤波器、谐振器、天线和波导等微波器件中的应用越来越受到人们的重视[1-5]。为了满足微波器件小型化和集成化的需要，低温共烧陶瓷（LTCC）技术被认为是一种很有前途的制备方法[6-8]。一般来说，需要具有低烧结温度（lt;960°C）、高质量因数（Qtimes;f）值和接近零的谐振频率温度系数（tau;f）的微波介电陶瓷[9-11]。近年来，AMoO4（A=Ba，Mg，Mn和Zn）陶瓷在半微波领域的应用已成为潜在的候选材料烧结温度低（900℃），相对介电常数低（7-9）和高质量因数（gt;30000GHz）[12-13]。然而，所有这些样品都显示出较大的负tau;f值（46 ppm/℃至87 ppm/℃），这不适合实际使用。谐振频率的近零温度系数可以确保微波器件在不同工作温度下的热稳定性[14]。为了达到零tau;f，有效的方法之一是加入其它具有相反tau;f值的化合物。金红石TiO2具有较大的正tau;f值（ 460 ppm/℃）[15]，已成功地应用于一些负温度系数谐振频率的微波介电陶瓷[16-20]。此外，复合陶瓷的混合行为对相对介电常数和tau;f值的调整有显著影响。因此，我们试图对（1-x）MgMoO4-xTiO2陶瓷系统进行全面的研究。

本文研究了（1-x）MgMoO4-xTiO2复相陶瓷的相组成、显微结构和微波介电性能。研究了微结构与微波介电性能的关系，提出了相对介电常数、Qtimes;f值和tau;f值的变化机理。

2.实验过程

以试剂级MgO和MoO3作为原料，采用固相反应法制备了MgMoO4复合物。以化学计量法对氧化物进行加权，随后在乙醇中球磨6小时，在红外线灯下干燥后，将混合物在700℃下在氧化铝坩埚中煅烧6小时。用球磨法将MgMoO4和TiO2粉末按以下公式混合12小时：（1-x）MgMoO4-xTiO2（x=0.0、0.1、0.2、0.3和0.4）。最后的粉末用7%的PVA制成直径为15毫米、厚度为7毫米的圆柱体素胚，在550℃下排出粘合剂后，样品在950℃下在空气中烧结5小时。

样品的晶体结构由X射线衍射仪（日本Rigaku Ultima IV）在2°至60°的Cu Ka辐射下进行鉴定。采用场发射扫描电子显微镜（FE-SEM，德国蔡司梅林紧凑型）分析抛光和蚀刻表面的微观结构。用阿基米德方法测量了样品的体积密度。使用网络分析仪（Agi-lent，8720ES，Santa Clara，California）测量了烧结样品的微波介电性能。

分别用Hakki-Coleman法和屏蔽腔法测量了相对介电常数和空载Q值。谐振频率的温度系数是在25°C–85°C的温度范围内使用下列公式确定的：

tau;f=（f2-f1）*10^6/f1（85-25）（ppm/℃） （1）式中，f1和f2是25°C和85°C时的谐振频率。

3.结果与讨论

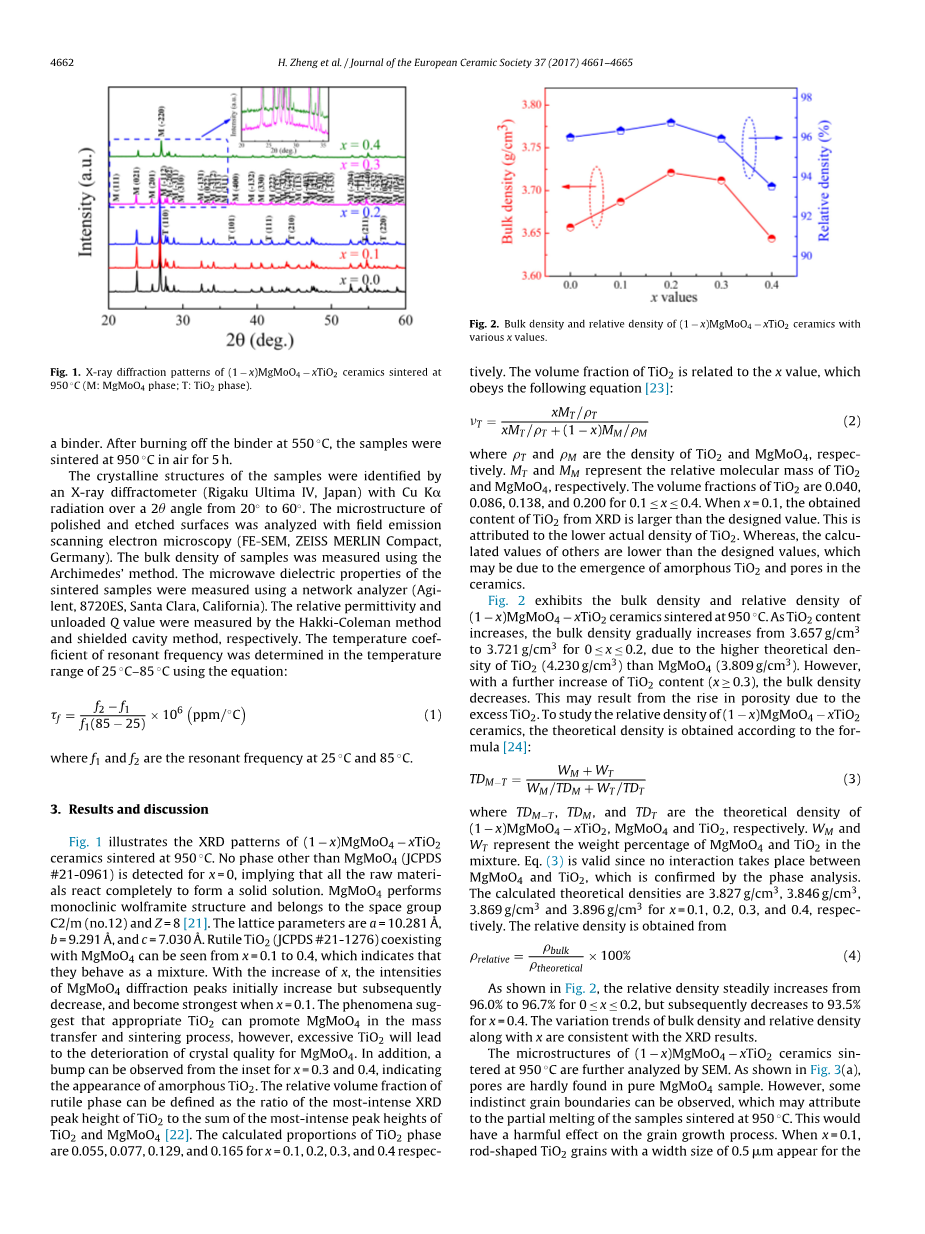
图2.不同x值的（1-x）MgMoO4-xTiO2陶瓷的体积密度和相对密度

图1.950℃烧结（1-x）MgMoO4-xTiO2

陶瓷的X射线衍射图（M:MgMoO4相；T:TiO2相）

图1显示了950℃烧结的（1-x）MgMoO4-xTiO2陶瓷的XRD图谱。除MgMoO4（JCPDS#21-0961）外，未检测到x=0的相，这意味着所有原料完全反应形成固溶体。MgMoO4具有单斜的黑钨矿结构，属于C2/m空间群（no.12）和z=8[21]。参数为A=10.281，B＝9.291，ANC为7.030，RuTiLeTiO2（JCPDS 211-1276）共存。当MgMoO4从x=0.1到0.4时，MgMoO4的扩散峰先增大后减小，当x=0.1时最强。这一现象表明，适当的TiO2在传质和烧结过程中促进了MgMoO4的生成，但过量的TiO2会导致MgMoO4晶体质量的下降。此外，在x=0.3和0.4时，可从插图中观察到凸起，表明出现非晶TiO2。金红石相的相对体积分数可以定义为TiO2最强烈的XRD峰高与TiO2和MgMoO4最强烈峰高之和的比值[22]。TiO2相的计算比例分别为0.055、0.077、0.129和0.165，对应x=0.1、0.2、0.3和0.4。TiO2的体积分数与x值有关，x值遵循以下方程式[23]：

VT=（xMT/rho;T）/rho;T （1-x）MM/rho;M （2）

式中，rho;T和rho;M分别为TiO2和MgMoO4的密度，MT和MM分别代表TiO2和MgMoO4的相对分子质量。TiO2的体积分数分别为0.040、0.086、0.138和0.200，当0.1le;xle;0.4时，当X射线衍射（XRD）为0.1时，TiO2的含量大于设计值，原因是二氧化钛的实际密度较低。而其他材料的计算值均低于设计值，这可能是由于陶瓷中出现了非晶态TiO2和孔洞。

图2显示了950℃烧结的（1-x）MgMoO4-xTiO2陶瓷的体积密度和相对密度。随着TiO2含量的增加，由于TiO2（4.230 g/cm3）的理论密度高于MgMoO4（3.809 g/cm3），体积密度从3.657 g/cm3逐渐增加到3.721 g/cm3（0le;xle;0.2）。然而，随着TiO2含量的进一步增加（xge;0.3），体密度降低，这可能是过量的TiO2导致孔隙率上升所致。为了研究（1-x）MgMoO4-xTiO2陶瓷的相对密度，根据公式[24]得出理论密度：

TDM-T=（WM WT）/（WM/TDM） （WT/TDT） （3）式中，TDM-T、TDM和TDT分别为（1-x）MgMoO4-xTiO2、MgMoO4和TiO2的理论密度，WM和WT表示混合物中MgMoO4和TiO2的重量百分比。式（3）是有效的，因为MgMoO4和TiO2之间不发生相互作用，这由相分析确定。当x=0.1、0.2、0.3和0.4时，计算的理论密度分别为3.827g/cm3、3.846g/cm3、3.869g/cm3和3.896g/cm3。相对密度从下式获得：

rho;relative=rho;bulktimes;100%/rho;theoretical （4）

如图2所示，对于0le;xle;0.2，相对密度从96.0%稳步增加到96.7%，但对于x=0.4，相对密度随后下降到93.5%。体积密度和相对密度随x的变化趋势与XRD结果一致。

图3.950℃烧结的（1-x）MgMoO4-xTiO2陶瓷的扫描电镜图像：

（a）x=0，（b）x=0.1，（c）x=0.2，（d）x=0.3和（e）x=0.4

利用扫描电镜进一步分析

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[245667]，资料为PDF文档或Word文档，PDF文档可免费转换为Word

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章