英语原文共 7 页,剩余内容已隐藏,支付完成后下载完整资料
超快二维核磁共振数据的压缩感知和重建:原理及其生物分子应用
摘要:当前,对二维核磁共振的积极研究主要涉及了获取该光谱所需的最小扫描频率,尤其是当其受采样而非灵敏度因素控制时。在研究中,我们未采用间接域监测的常规采样方法,而是使用了非均匀采样和迭代重建算法来减少最小扫描频率,也可通过振荡场梯度,从空间上对间接域信息进行编码,并在此基础上用“超快“方法来压缩二维核磁共振的最小扫描频率,以此得到最小频率。鉴于超快核磁共振可同时记录间接和直接域数据,因此该实验结合了这些正交域的频谱限制——通常要求使用强采集梯度和大滤波宽度以实现各谱维数上的所需带宽和分辨率要求。本研究将空间编码与迭代重建方法相结合,讨论了缓解这些要求的方法,由此提高方法性能和适用性,并根据二维HSQC超快核磁共振数据的生物分子压缩感知重建,给出了该原理的示例,示例表明,该方法能将这类实验所需的梯度强度降低80%以上。
关键词:超快二维核磁共振;非线性重建;压缩感知;生物分子光谱
1、前言
二维核磁共振(2D NMR)为分辨和鉴别各种化学和生化系统中的化学位点性质提供了宝贵信息,二维光谱数据采集模式由Jeener、Ernst及其同僚[1,2]提出,并用于记录自旋系统发出的信号(将自旋系统作为两个独立时间变量(t2——与直接物理测量相关的运行时间变量;t1——整个独立实验系列上系统性递增的参数延迟)的函数)。通过快速傅立叶变换(FT),从该二维时域矩阵检索光谱信息,最好用均匀采样的时间变量来实现,然而,这种采样带来了一个约束因素——即:由于映射到相应间接域所需的每个参数增量△t1与独立扫描有关,因而,根据N1=SW1/△v1,所需的最少实验次数N1是由间接域光谱宽度(SW1=1/△t1)及相关的光谱分辨率(△v=1/t1max=1/N1△t1)决定的。该约束因素起源于实际采样数据形式所构成的需求,而非由信噪比(SNR)因素所导致。因此,为绕过该约束,并减小扫描所需的最少次数N1,研究者提出了各种策略,这些策略的主要思路取决于由先验一维核磁共振测量中获取的光谱信息的开发,并用其对沿v1间接域上的谱峰进行选择性寻址[3,4],或根据后处理从镜像的光谱窗口对其进行展开[5]。另一组方法旨在完全摆脱传统的尼奎斯特时域采样准则,来重建所关注的光谱。例如,利用维度简化的测量[6-8]或间接域的非均匀采样,并用非快速FT算法对其结果进行处理[9-13]。后者算法包括:最大熵、最大似然、频率分解以及一些用正则化形式来稳定那些可能会成为病态反演问题的方法,所有的这些方法都是基于通常可实现的这样一个前提——即:极高的敏感性,间接域内的谱线数量要远远小于FT范式所需的扫描次数。
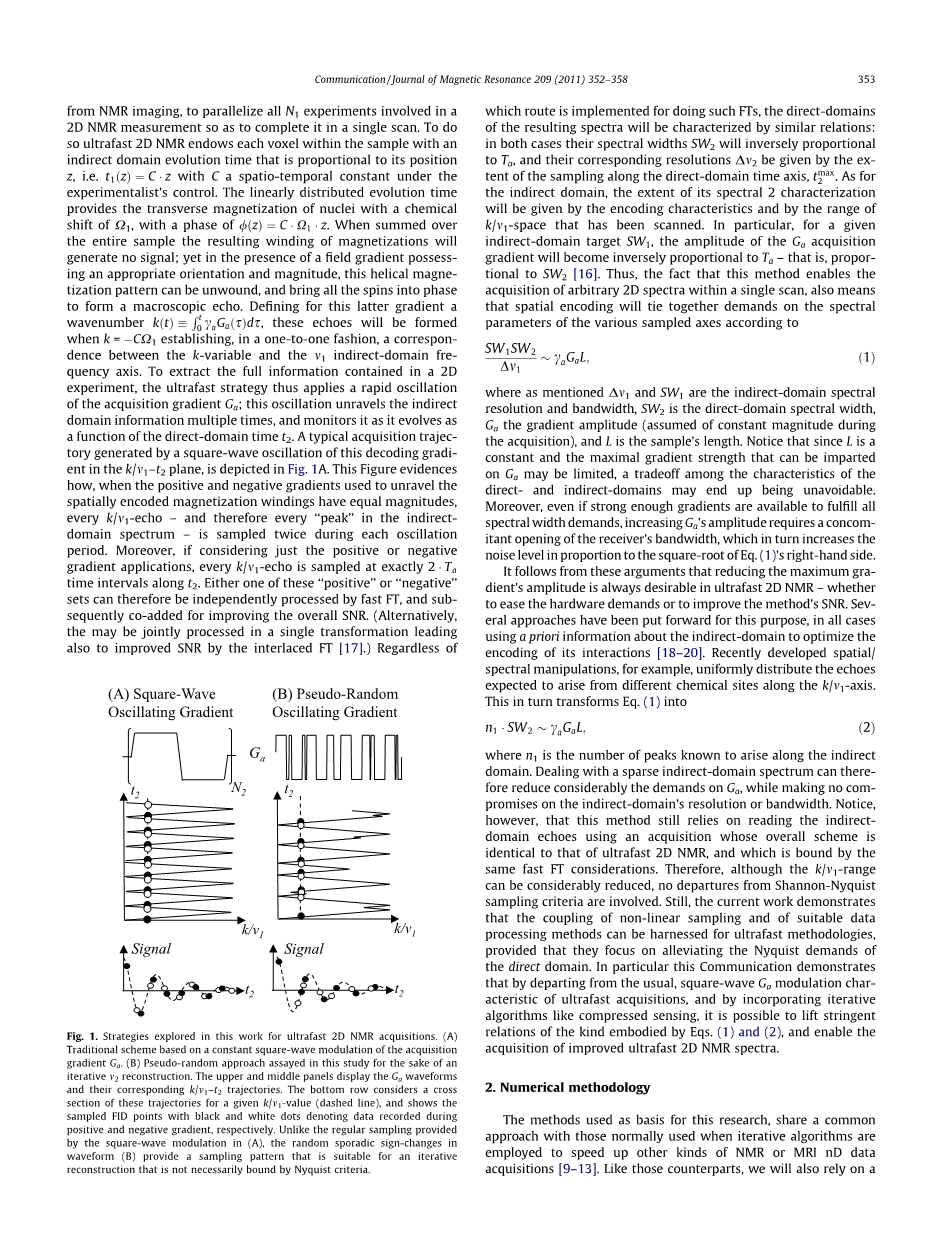
近年来,出现了一种“超快”算法以替代以上方法[14-16],该算法从不同角度减少了二维光谱所需的总扫描次数,这些方法依赖于NMR图像的衍生概念,将二维NMR测量中的所有N1试验并行起来以在单次扫描中完成。超快二维NMR给样品中的每个体素赋予了间接域演化时间,在实验者控制下,该时间与与其位置z成正比,即:t1(z)=C.z,这里,C为时空常量。线性分布的演化时间为 胞核的横磁化提供了化学位移Omega;1,其相位为:Phi;(z)=C.Omega;1.z,对整个样本求和,当所得的磁化绕组不产生信号时,在带有适当方向和幅度的场梯度存在的情况下,可解除该螺旋式磁化模式,并将所有自旋带入相位中,以形成宏观回波。定义后者梯度的波数,当k=-COmega;1建立时,会形成这些回波,在一对一模式下,k变量和v1间接域频率轴之间是对应关系,为提取二维试验中的完整信息,超快策略使用了一个采集梯度Ga的快速振荡,该振荡多次解开了间接域信息,并在其成为直接域时间t2的函数时,对其进行监测。图1A描绘了k/v1-v2平面中,该解码梯度的方波振荡生成的典型采集轨迹,该图证实了,用于解开空间编码磁化绕组的正、负梯度是如何及何时具有相等幅值的,每个k/v1回波——即间接域光谱中的每个“波峰”——在每次振荡周期内采样两次,此外,如果只考虑正、负梯度应用,则在t2的确切时间间隔2.Ta上对每个k/v1进行采样,正、负集中的任何一个均可由快速FT独立处理,并同时添加,以提高整体SNR。(另外,也可通过交错FT在单一的主导转化中共同处理以提高SNR[174])。无论用何种思路进行傅立叶变换,所得光谱的直接域都将用相似的关系——即: 其光谱宽度SW2与Ta成反比,且其相应分辨率△v2可由直接域时间轴上的采样度t2max给出——来表征。对于间接域,其光谱2的表征度可由编码特征和已扫描的k/v1空间范围给定,特别是对于给定的间接域目标SW1,Ga采集梯度的幅度与Ta成反比——即:与SW2成正比[16]。因此,该方法可在单次扫描内采集任意二维光谱,这也意味着,根据下式,空间编码与所需求采样轴光谱参数是相关联的。
图1 本研究所探讨的超快二维NMR采集策略。(A)基于采集梯度Ga恒方波调制的传统方案。(B)本研究所用的伪随机方法以进行迭代v2重建,上面板和中面板显示了Ga波形,及其相应的k/m1–t2轨迹,最下面一行认为是给定k/v1值(虚线)的轨迹横截面,并显示了所采样的FID点——黑点和白点分别表示正、负梯度期间所记录的数据。和(A)中方波调制所提供的常规采样不一样,波形(B)中的随机分散的符号变化提供了一个可用于不受尼奎斯特准则限制的迭代重建的采样模式。
这里,n1为间接域上出现的已知峰的数量,因此,无须损失间接域分辨率和带宽的同时,处理稀少的间接域光谱可很大程度减少对Ga的需求,但须注意的是,该方法仍取决使用整体方案等同于超快二维NMR的采集方法所读取的间接域回波,且该方法受限于相同的快速FT因素,因此,虽然极大的减小了k/v1范围,但并未脱离香农-尼奎斯特采样准则,该研究表明,超快方法可利用非线性采样和恰当的数据处理方法间的耦合,只要它们着重于减缓直接域的尼奎斯特要求。这种通信尤其表明了,脱离了超快采集的一般方波Ga调制特征,并通过压缩感知这类迭代算法结合,可解除等式(1)和(2)所表达的严格的关系种类,并采集改进后的超快NMR光谱。
2、数值方法
作为本研究的基础,这些方法与那些用迭代算法加快其它类型的NMR或MRI nD数据采集时常用的方法之间有着共同的途径[9-13],和其它研究者一样,本研究也是基于非均匀采样模式和数值算法,该算法将光谱检索过程从快速FT带来的约束中解放出来,在传统的nD NMR光谱/成像中,数值算法可根据远远小于香农准则所要求扫描采集来重建频域数据,然而,在快速NMR/MIR光谱中,扫描次数已减至最小值,因而加速目标已不再适用了。此外,由于空间编码域上缺乏傅立叶变换,因而,通过数值方法提取间接域光谱也不适用。不过,可利用非傅立叶变换方法带来的额外灵活性来实现另一目的:减少解码梯度的幅度Ga,并由此减缓前面提到的技术和灵敏度问题,这反过来也意味着,t2轴上迭代重建方法的应用是在这些梯度上操作的,在处理二维NMR的直接域前,就我们所知,并未应用这类程序——由于来到这里的信息在时间和灵敏度上几乎是“无偿的”。然而。等式(1)所提出的Ga和SW2的这种耦合,让我们考虑到了在超快NMR直接域上使用非FT方法所带来的后果。
摆脱快速FT处理所施加的准则,所需的一个基本步骤是放弃使用等间隔数据采样模式:只有这样才能避免频率混淆,并能在不受尼奎斯特限制的范围上,从时域响应中提取真正频率[26]。由此可见,常用于超快NMR(图1A)中的波形不再具有以下作用——即:通过给每个k/v1回波提供沿t2上的均匀采样模式,这种周期性的Ga方波不会实现如非FT处理所需的随机时域点阵列。但是,通过一个施加到梯度波形的伪随机符号变化,可轻松的引入非均匀t2模式。由于k/v1轴需探测预定义的频率间接域范围SW1,因而这种变化不是完全随机的,因此,为适当覆盖到给定的目标间接域光谱区域,需定制Ga上的变化。图1B阐述了实现这一点的途径之一,即:利用电势梯度及其在k/v1-t2空间内所得的轨迹。对于k/v1轴上的每个坐标——沿t2方向上随机分布点的个体集合(图1B,底部),我们对FID过程中的采样点进行了适当的重排,然后,对k/v1上的每个坐标进行迭代计算,以重建直接域上产生的相关1D光谱,并由此寻求完整的二维分布。
这里,对预期的二级光谱进行压缩感知重建[13,21–25],在此基础上,我们探讨了该方法的结果——即使也可使用其它方法[9–12,27]。压缩感知取决于若干基本假设,其中之一是:所寻求的光谱信息是稀疏的,即:目标范围内的多数频率坐标不含有任何信息,作为整体的一维直接域NMR光谱很少能实现这一前提,但仅在处理完整的二维干涉图时,该前提通常是有效的,由此,将待重建的数据分成构成整个二维分布的、众多的k/v1。所寻求的每个一维直接域光谱可通过将其相应的FID匹配到函数S上来进行重建,且概率极高,并由此完成l-范数的最小化:
这里,,等式(3)中的算子表示光谱S的傅立叶变换,它考虑了一系列任意直接域时间{tp}上采样的对应FID,为解决这一数值拟合问题,研究人员提出几种方法,本研究实现了一种基于迭代软阀值[13,23]的最简方法,为评估光谱分布S,该算法进行了一系列的迭代,并仅保存在每个明显区别于潜在数值或热噪声的光谱分量中,随后,在算法中加入这些“波峰”以重建光谱,并根据下式所定义的阈值算子滤掉残留光谱。考虑了:
如果特定yq值的残留光谱输入小于阀值lambda;,此该操作返回零,否则减小其幅值,并保持输入原始相位,可计算出重建光谱所生成的预期FID,并从初始FID减去该预期FID,将结果作为后续迭代的输入,本研究用该算法的伪码来还原来完整的二维空间编码光谱,如表1所示。
表1 超快二维NMR数据迭代软阀值处理伪码
图2 (A)测得的常量时间、空间编码的HSQC序列方案,这里所用的所有时序和梯度强度值分别用单位ms和G/cm表示;通过强清除梯度脉冲实现水抑制,采集停留时间设为2mu;s,遵循每个梯度循环,将硬6mu;spi;脉冲用于15N解耦,为实现间接域上的高分辨率,实验使用了较长的20ms的编码周期。(B)在信号平均扫描四次,并显示在50%的等高线上时,使用传统的plusmn;Ga方波采集梯度在泛素水溶液上获取纯吸收的二维光谱、正梯度数据集仅由零填充以及t2和快速FT方向上具有30cm衰减时间的指数切趾法来处理,鉴于所使用的强大采集梯度,接收器带宽也相应地设为gamma;aGaL=290 kHz (L = 1.8 cm)。(C) 和(B)一样,但信号平均扫描十六次,并显示在40%的等高线上。(D) 和(B)一样,但是将数据进行迭代重建,该采集中所用的梯度波形如面板(E)所示,同时还显示了形成k/v1-ts面板的非周期轨迹,实际Ga(t2)波形包含了16mu;s的上升/下降时间,以及每隔634mu;s、通过硬pi;脉冲进行15N解耦的零梯度周期,通过提升快速FT的严格采样要求,整体|Ga|强度降低至7.5G/cm,随后,接收器的带宽下降也使得仅通过四次扫描即可重建高质量光谱:(D)中数据显示在25%的等高线上。从相应的四次扫描实验转换而来的指定间接域中提取横截面(F),并由此阐释两次变换引起的光谱SNRs间更明确的比较。该光谱重建包括:根据表1,用mu;=0.9迭代拟合到分辨率为6Hz的plusmn;1.2 kHz光谱区域上,250次迭代后,终止拟合(增加迭代次数并不会引起二维光谱的显著变化),完成后,所得向量为直接域上的逆FT,以30ms的指数衰减加权,将正FT提供给最终光谱,双核2.2GHz的CPU处理这类数据集所需的总时间不超过60s。
成功实现压缩感知重建的另一个要求是确保每个k/v1值有充足的t2点数量。事实上,如果该点集合远大于每个k/v1坐标的直接域上出现的非等价波峰数量,则会出现v2 光谱的适当表征。须指出的是,不能同时测量不同的k/v1,需用相同的Ga物理梯度分步研究不同的k/v1坐标,所使用的Ga强度是有限的,因而,过度集中于k/v1轴的某一个区域则会降低k/v1其它区域上的采样性能。和T2弛缓(即:在可用的最大采集时间上设置一个限制)存在的情况一样,该约束意味着应选择平均循环周期大于每个采样k/v1坐标的连续梯度波形来开发这类处理策略,要实现这一点取决于传达变化Ga的较小随机因子,即从常规方波调制周期2Ta中加上或减去该值。本研究中,计算梯度波形方向上任意点的符号切换时机仅被假定在0.1%-0.2%范围内,这将产生图1B所示的波形和k-t2空间轨迹。当然,研究中的光谱越稀疏,则参数选择越灵活,可用的随机因子也越大。这反过来又产生了可用比传统FT快速二维NMR方法中更弱的梯度来检索的光谱,通过下列实验结果可阐释其质量优势。
3、实验
为证实超快二维NMR中的压缩感知重建的潜在优势,我们分析了溶于90%/10%H2O/D2O缓冲液中、aasymp;2mM 的富集15N的泛素样品,利用14T磁体和配备了单线性z梯度的三通道探头的VNMRS光谱仪,将具有常量时间和空间编码的二维HSQC NMR实验记录在该样品[16,28]上。用方波采集梯度执行常规超快二维NMR实验,并作为参考,生成定制波形,并用于迭代光谱重建实验,所有波形及其辅助RF脉冲和数据处理算法都用定制的Matlab程序,根据要求编写。
4、结果
对目标8.5 kDalton的蛋白质上进行二组压缩感知HSQC NMR实验,其目的是展示开发迭代过程所带来的灵敏度方面的优势,这两组实验不同于所使用的最大编码周期t1max的持续时间:编码越长,间接光谱域的分辨率就越高,但所需的Ga梯度也越大(参见等式(1)),因而SNR也越小,图2阐释了如何用新方法绕过该惩罚,并将其作为测试用例,以此讨论了具有较长编码周期(20 ms, Fig. 2A)的序列。给定t1max和光谱带宽,可用较大的|Ga|asymp;38G/cm方波梯度来
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[151636],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。