
英语原文共 4 页,剩余内容已隐藏,支付完成后下载完整资料
本科生毕业论文(设计)
文献翻译
英文题目 Determination of Propagation Constant Using 1D-FDTD with MATLAB
中文题目 使用1D-FDTD与MATLAB的传播常数的确定
使用1D-FDTD与MATLAB的传播常数的确定
摘要 : 本报告主要集中在使用传统的MATLAB代码通过1D-FDTD确定诸如微带线和共面波导(CPW)之类的平面传输线的传播常数。 除此之外,本文介绍了基本现象的研究,如在两种介质之间的界面处的反射和材料吸收体的设计。 沿着线Y = Z = 0模拟场Ey和Hz,即沿着X轴的传播。 研究了源(高斯脉冲,正弦)的实现以及各种边界例如Mur ABC,PML对入射/散射/总场的影响。 还提出了使用CST微波工作室和MATLAB的相位常数的比较图.
关键字:DD-FDTD,微带线,CPW,Mur ABC,PML,高斯脉冲,正弦。
一.介绍
有限差分时域(FDTD),差分类型时域方法的数值方法是一种通用的方法,几乎不需要预处理麦克斯韦方程以获得控制方程[1]。它直接近似于麦克斯韦卷积方程中的微分算子,在空间和时间上交错的网格上。 FDTD方法进展的动力由Kane Yee的独特贡献提供[2]。我们选择MATLAB编码,因为图形程序的综合库。这对于理解FDTD算法的工作经常是关键的。 E和H场在网格上计算,具有前进时间,时间离散化,其中场分量相对于彼此偏移plusmn;5ଶ并且E&H场在时间上相差1ଶ时间,其中Delta;x和Delta;t分别是空间和时间离散[3]。本文通过逐步过程解释了上述过程:第二部分描述了通过考虑X方向上的传播将3D Maxwell方程式减少到1D形式。第三节描述和验证吸收边界条件(ABC)。第四节描述了两种介质之间的电场的透射和反射。第五节用CST Microwave Studio描述和验证结果,传播常数(beta;)。
二.公式
将3D Maxwell方程式简化为1D。在一维FDTD的情况下,我们假设TEM波沿着X方向传播(J = 0),3D麦克斯韦方程为:
在1D FDTD的情况下,我们假设TEM波传播沿X方向
从指向定理,波传播沿X方向则E场在Y方向,H场在Z方向。在利用上述假设求解方程式(1)和(2)
替换(4)中(3)的部分空间导数,反之亦然产生一维波动方程。
其中表示 或 在自由空间中,= 并且(5)采用熟悉的形式,
其中真空中的光速[4]。
B. 1D时间更新方程。在FDTD分析中,公式(3)和(4)差分近似。 中心差分方程为用于最高精度,由[5]定义,
所以,具有二阶精度。以(7)的形式表示等式(3)和(4),
其中i和n是表示空间和时间的整数分别。 时间先进方程是
上面的表达式可以在MATLAB中编写如下,
C.电网的激励(源)高斯脉冲[6]经常用于FDTD,因为它平滑振幅变化和大频率含量。
其中=脉冲中心,T =脉冲宽度。
如果是正弦源那么
III 边界条件
穆尔的第一阶吸收边界条件。如果沿-x方向传播的平面波就是这样波在x =恒定平面处将不遭受反射
泰勒的系列扩展
并施加Delta;x=cDelta;t(考虑稳定极限)和求解,在节点N 1或在最后E场节点的Mur的边界权利是[7]。
将Mur的边界放置在node1或第一个E场节点在左边是
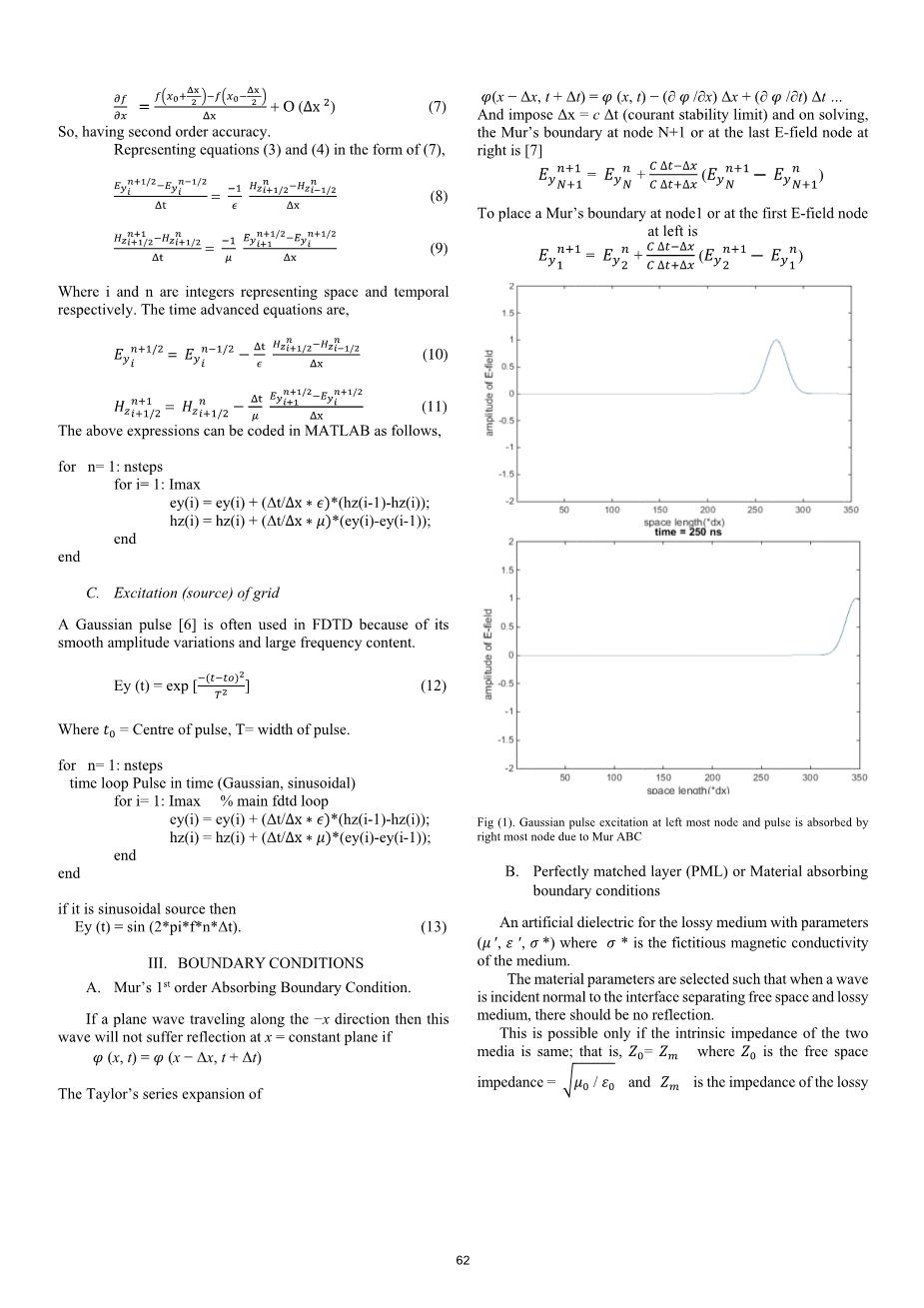
图(1) 高斯脉冲激发在最左边的节点和脉冲被吸收最右边节点由于Mur ABC
完全匹配层(PML)或材料吸收边界条件一种用于有损介质的人工电介质其中 是虚构的磁导率的介质。材料参数被选择为使得当波垂直于分离自由空间和有损耗的界面介质,应该没有反射。这只有在两个固有阻抗的情况下才是可能的媒体是相同的; 也就是说,其中是自由空间阻抗= 和是有损耗的阻抗介质定义为解决,匹配条件给出。可以从适当的范围计算的。 因此,具有PML的更新方程是[8]。
图(2)CW正弦波的传播并被材料吸收体吸收
IV 接口处的反射
通过包括电导率和介电常数介质,更新方程由下式给出:
图3(3)均匀振幅脉冲入射通常在电介质上(=4)从自由空间,反射脉冲幅度= 0.33&透射脉冲= 0.66。
图(4)CW正弦波(f = 50MHz)通过分层介质的传播
参数= 15cm,= 0.5。 节点在i = 250,分离真空(= 1,= 0)和有损电介质(= 4,=0.001S)。 相位常数可以根据指导来确定波长,它是。 从上图,两个连续峰之间的距离分别给出中。
V.结果
A.微带线的beta;(Rad / m)对频率图
图(5)微带线具有线宽W = 2mm,衬底= 1.6mm,= 2.2
图6使用FDTD和CST的上述微带线的beta;的比较微波工作室
- CPW的beta;(Rad / m)对频率图
图(7)具有迹线宽度= 1.6mm,间隙= 2mm的共面波导(CPW)= 2.2,基板厚度= 1.6mm
图(8)使用FDTD和CST微波的上述CPW的beta;的比较工作室。
VI 结论
本文成功展示了其的决心传播常数(beta;)通过使用FDTD算法的帮助的MATLAB。还有反射和透射现象电磁波在两种介质之间的界面处。
致谢
我要感谢S. Raghavan教授的教授提出的建议。
参考文献
[1] Ramesh Garg,“Analytical and Computational Methods in Electromagnetics”ARTECH HOUSE,INC,2008.
[2] K. S. Yee,“Numerical solution of initial boundary value problems involving Maxwells equations in Isotropic media”天线传播。 vol。
[3] Tatsou Itoh,“Numerical Techniques for Microwave and Millimeter-Wave Passive Structures”,A John Wiley&Sons,INC。,Publications,1989.
[4] Hung Loui,“1D - 使用MATLAB的FDTD“,ECEN-6006数值方法在光子学项目-1,2004年9月
[5] David B Davidson,”Computational Electromagnetics for RF and Microwave Engineering“,Cambridge University Press,2005.
[6] EW Weisstein,”Gaussian函数“Math World-A Wolfram Web:Resource,http://mathworld.wolfram.com/GaussianFunction.html, 2004.
[7] A.Taflove和S.Hagness,Computational Electrodynamics - the finite difference time-domain method,第2版。 Norwood,MA:Artech House,2000 [8] R.R.McLeod,“Finite difference time domain class notes,”pp.31-59,Sept。 2004年
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[28302],资料为PDF文档或Word文档,PDF文档可免费转换为Word


