
英语原文共 4 页,剩余内容已隐藏,支付完成后下载完整资料
使用信号规律分析来鉴别心内膜电图解组
摘 要
从非线性动力学理论出发,对复合分心房电图(CFAE)进行了分析,以表征其生理动力学行为。根据A-EGMs信号规律性,将113个短期心电图(A-EGM)按三个专家注释为四类分级,得出结果。对A-EGM信号采用以下措施:一般相关维度,近似熵,偏差波动分析,Lempel-Ziv复现和Katz-Sevcik,方差和箱体计数分形维数。通过Kruskal Wallis统计检验来评估混乱。除了偏差波动分析和方差分形维数外,即使对于低显着水平alpha;=0.001,CFAE分解也被认为具有统计意义。此外,A-EGM信号的复杂性越来越高,通过1阶通用相关维数和近似熵的较高值反映出来。
第1章 引言
报道,产生复杂分次心房电图(CFAE)的心内膜位点是治疗心房颤动(AF)的消融靶点[1]。为了识别这些网站,已经做出了巨大的努力来描述AF[2]中激活的模式,并量化CFAE在时域或频域中的一般特征[3]。然而,CFAE识别的过程高度依赖于操作者的判断。此外,不清楚CFAE是否是局部心房电图混乱的随机过程或重现的生理效应[4]。本研究旨在应用信号规律分析来描述A-EGM分级水平的时空变化。该分析使得能够研究A-EGMs的非线性动力学,并且确定了高水平的A-EGM分馏也被更高的规律度量值所反映的假说。
第2章 方法
2.1 实验数据集
采用4mm灌注消融导管(NaviStar,Biosense-Webster),采用持续性房颤患者12例(9例男性,年龄56plusmn;8岁)收集心房双侧心电图。采样频率为977Hz。A-EGMs的113个被专家手工选择和裁剪。为了研究的目的(见图1),设定了四个分级分类(CF)。数据集排名由三位独立专家完成,总共排名339(113*3=339)。三位独立专家从来不会因为不止一个邻国CF而不同意排名。因此,最流行的模式被选为最终得分。这四个CF能够得到每个类别中具有显着数量样本的A-EGM的统一数据集(class1:C1=22,class2:C2=42,class3:C3=36,class4:C4=13),以便这样的数据集可以用于规律性分析[5],[6]。
图1,四个复杂分级心房电图的时代。这些是研究中使用的每个CF的代表。从上到下:i)class1:有组织的活动,ii)class2:轻度分馏。 iii)class3:中等分馏度,iv)class4:高分馏。
2.2 规律性信号措施
在尝试计算心内膜电图的分形维数之前,建立证据表明这些波形可以表征为分形是重要的。分形维数值与模式的规律性有关,或者嵌入在模式中的信息量形态,熵,光谱或方差[7]。考虑到A-EGMs的形态特征,似乎这些信号具有有效的分形维数值,主要是由于两个原因。首先,信号不会自交。通过查看图1中的任何一个A-EGM波形,很明显,为了缩放它,每个轴需要不同的缩放因子。这表明A-EGM波形是自发的。第二,信号表现出明显的准周期性,因为它们从自然重复过程(特别是心跳)出现。在下一小节中,我们将描述本研究中使用的信号规律性度量。
2.3 一般相关维度
1)参数选择和信号嵌入:只使用一个变量的时间序列作为输入,但是这个时间序列数据用于重建多维嵌入空间[7]。有必要确定以下三个参数:i)采样值之间的时间延迟,ii)连续向量之间的时间间隔和iii)嵌入维度。
使用自动相互信息估计采样值之间的时间延迟。自动相互信息的第一个最小值是时间序列吸引子重建的首选值[7]。连续向量之间的时间间隔设置为等于采样时间。在这种情况下,向量的数量等于时间序列中的样本数减去嵌入维数[7]。
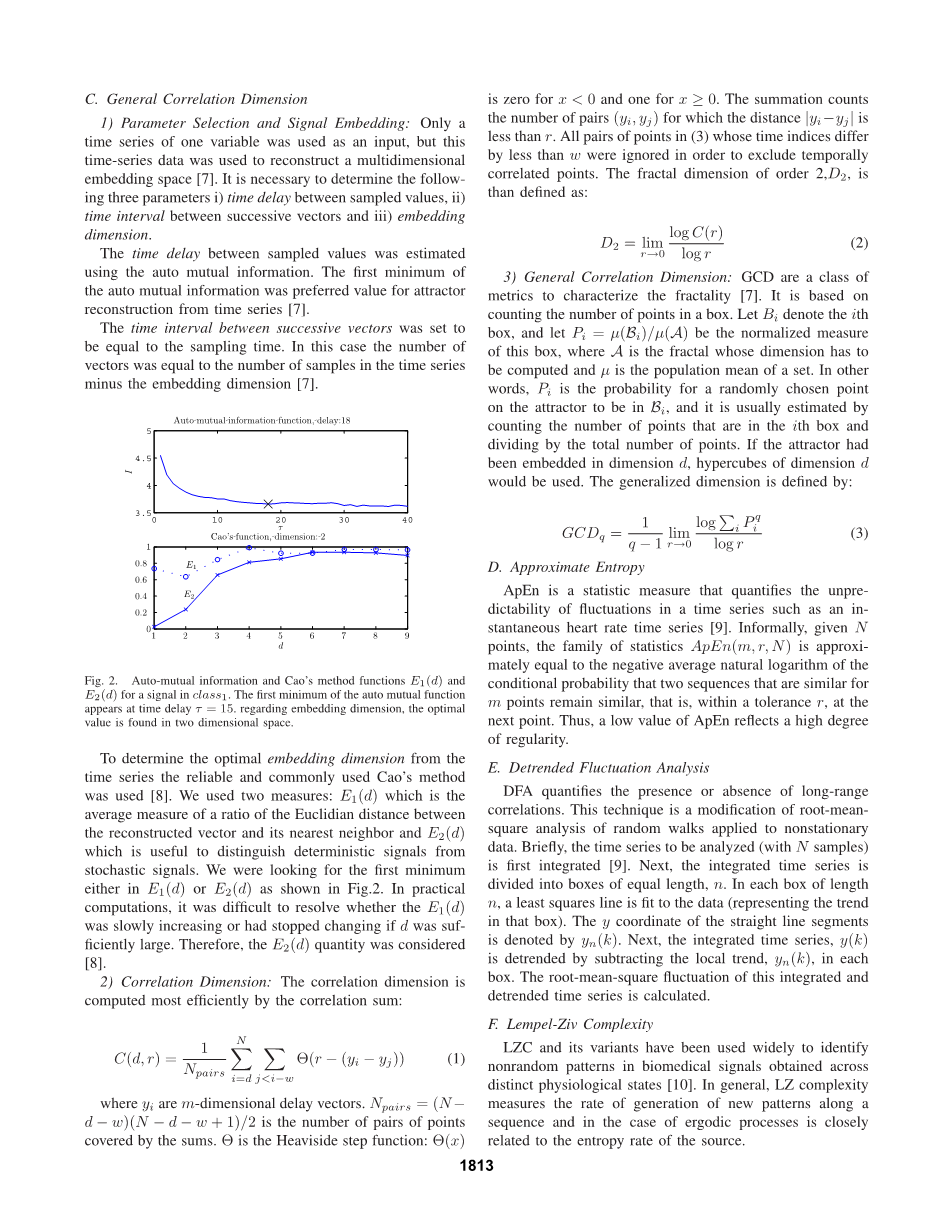
为了从时间序列确定最优嵌入维数,采用可靠且常用的Cao方法[8]。我们采用两种措施:E1(d)是重建矢量与其最近相邻的欧几里德距离与E2(d)的比值的平均值,用于区分确定性信号与随机信号。我们在E1(d)或E2(d)中寻找第一个最小值,如图2所示。在实际计算中,如果d足够大,则E1(d)是否缓慢增加或停止改变是困难的。因此,E2(d)量被认为是[8]。
图2.对于1类信号,自相互信息和Cao方法的功能E1(d)和E2(d)。自相关函数的第一个最小值出现在时间延迟T = 15。关于嵌入维度,最优值在二维空间中找到。
2)相关维度:相关维数通过相关和最有效地计算:
(1)
其中yi是m维延迟向量。Npairs =(N-d-w)(N-d-w 1)/ 2是由和覆盖的点对数。theta;是Heaviside阶梯函数:对于x lt;0,theta;(x)为零,而对于xge;0,theta;(x)为零。求和距离|yi-yj|的对(yi,yj)小于r。忽略时间指数小于w的(3)中的所有对点,以排除时间相关点。阶数2,D2的分形维数定义如下:
(2)
3)一般相关维度:GCD是一类用于表征分形度的指标[7]。它是基于计数一个框中的点数。令Bi表示第i个框,并且使Pi=mu;(Bi)/mu;(A)是该框的归一化度量,其中A是必须计算维的分形,mu;是集合的总体平均值。换句话说,Pi是吸引子上随机选择的点在Bi中的概率,通常通过计算第i个框中的点数除以总点数来估计。如果吸引子嵌入尺寸d,则将使用尺寸为d的超立方体。广义维度定义如下:
(3)
2.4 近似熵
ApEn是一个统计量表,用于量化时间序列波动的不可预测性,如瞬时心率时间序列[9]。非正式地,给定N点,统计数据ApEn(m,r,N)的数量近似等于条件概率的负平均自然对数,对于m个点相似的两个序列保持相似,即在容差r内,在下一个点。因此,ApEn的低值反映了高度的规律性。
2.5 偏差波动分析
DFA量化长距离相关的存在或不存在。这种技术是应用于非平稳数据的随机游标的根平均分析的修改。简而言之,要分析的时间序列(N个样本)首先被整合[9]。接下来,集成时间序列被分成等长的n个。在长度为n的每个框中,最小二乘线适合数据(表示该框中的趋势)。直线段的y坐标由yn(k)表示。接下来,通过减去每个框中的局部趋势yn(k),整合时间序列y(k)被去除。计算该积分和衰减时间序列的均方根波动。
2.6 莱姆-齐夫复杂性
LZC及其变体已广泛用于识别通过不同生理状态获得的生物医学信号中的非随机模式[10]。一般来说,LZ复杂度测量沿着序列产生新模式的速率,并且遍历过程的情况与源的熵速率密切相关。
2.7 Katz-Sevcik分形维数
用于获得分形维数的Katz-Sevcik算法主要基于形态学[11],并且计算为KFD=log10 n/log10 n log10 g/L其中n是KFD信号样本之间的增量数计算;L是连续增量之间的所有距离的总和;g是从第一增量开始测量的最大距离的值。必须指出,在计算KFD之前,执行沿信号的y轴和x轴的归一化。
2.8 方差分形维数
VFD由Hurst指数H确定,H的计算来自于分数布朗运动的性质[12]。该计算基于通过时间增量的动态过程产生的信号幅度增量C(t)的方差之间的幂律关系Delta;t=|t2-t1|,C(t2)-C(t1)表示为△C。幂律如下:Var[△C]〜△t2H其中赫斯特指数为:
(4)
具有嵌入欧几里德尺度E(对于A-EGM信号等于1)的过程的VFD由以下确定:VDF=E 1-H。
2.9 箱计数方法
计算集合分形维数的一种已知方法是方框计数方法(BFD)[13]。详细来说,对于Rd中的一组N点,以及长度为l的网格单元格中的空间分区,分形维数DB可以从下式中求得:
(5)
其中N(1)表示至少一个点占用的单元数。
2.10 统计评估
应用非参数Kruskal Wallis检验进行规律性比较。为了应对较少数量的A-EMG信号,使用了这种测试,特别是在第4类中,只有13个信号可用。
第3章 结果与讨论
使用规律性测量的A-EGM分馏评估的可靠性总结在表I中。每个类别报告了平均值和标准偏差值。通过实验10次试验和误差方法,发现ApEn,DFA和BFD的最佳参数设置。 在ApEn的情况下,公差参数r在保持图案长度m固定的同时增加0.05。考虑到DFA,用于定义两个DFA曲线的斜率的参数在每次运行中增加了4个。
最后,BFD尺寸dimBFD在每次运行中增加1个。导致10次运行中最小p值的最终参数如下:GCD:每个信号嵌入维度变量,应用Cao方法,时间延迟:每个信号的变量,自动交互信息被应用;ApEn:容差r=0.1,模式长度m=2;DFA:fast=2,mid=32,slow=64;BFD:尺寸dimBFD=5;LZC:使用二进制编码。
图3.所有类别的A-EGM分馏的平均广义尺度谱
图3显示平均广义尺度谱。谱应该是凸的,单调增加[7]。从一般维度qge;-2可以看出,班级之间的差异更为明显。特别地,对于广义维度q=-4,class3的GCD值大于class4的值。GCD测量在q=2处达到峰值,表明较高的嵌入尺寸qgt;2不能提供由于高维空间中出现数值误差而产生的可靠的辨别度量。为了指出使用较高的负相关维度的重要性,在表I中报告了q=-6,-5,2的GCD值。
我们对A-EGM信号的分形性质的假设由表I中的非常低的p值证实。即使显着性水平设置为alpha;=1e-3,大多数分形维数在区分AEGM类别组织方面具有统计学意义。DFA和VFD措施的例外情况。此外,与GCD1和ApEn测量相比,LZC,VFD和BFD测量具有较低的识别能力,如表I所示。主要原因是数据不足:A-EGM是采用977Hz的1.5s持续时间段的非常短的段,占1537个值。首先,如果输入数据集至少包含1000个样本,则ApEn能够正常工作[9]。第二,主要是通过仔细选择算法参数来实现良好的区分,特别是在应用自相互作用和Cao方法的GCD测量的情况下。
图4.使用相关维度和近似熵评估A-EGM分馏。 水平线代表每个类的平均值。
我们根据统计测试的结果比较了两个最佳表现尺寸:1阶和近似熵的一般相关维数,见表I中的粗体值。对数据集中的所有A-EGM信号计算分形维数。第1号的一般相关维度如图1的上部所示,第一个和最后一个类被GCD1值分隔开,请注意,中间类2和3部分重叠。从图4的下部可以看出,在ApEn的情况下,与GCD1尺寸相比,第2类和第3类的分离较。
第4章 总结
在AF的导管消融时代,AF期间描述A-EGM的初步尝试主要是基于心房信号的频域分析[3]。不仅主要频率(DF),而且A-EGMs分级的水平可能是临床上重要的局部心房信号描述[1]。具有高分馏A-EGM的场地几乎完全包含高DF的场地,而相反的场合并不总是如此。因此,开发可以评估A-EGMs规律性的其他措施是非常重要的,特别是区分低A-EGM分馏(LF)与高分馏(HF)。本研究揭示了所有选择分馏中A-EGM中存在非线性动力学水平。图4报告说,随着AEGM信号的复杂性日益增加,规律性措施的价值也越来越高。在所有水平的A-EGM分馏中,使用规律性测量的鉴别在显着性水平fi=0:001时发现统计学显着。提出的复杂措施成功地将C1类(LF)与A-EGM信号的C4(HF)分离。然而,中间类2和3之间的分离不是很清楚。其中一个原因是通过对3名专家的分类进行平均,以获得半连续的分级分级来定义这些分类。在某些情况下,很难将A-EGM信号分配到2类或3类。
对于未来的研究,所选择的复杂措施(GCD1和ApEn)可用作自动化和运营商独立系统的附加功能,有助于AF衬底烧蚀[5]。
致 谢
该项目得到
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[485853],资料为PDF文档或Word文档,PDF文档可免费转换为Word
以上是毕业论文外文翻译,课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。


